A uniform block of mass M and dimensions as shown in the figure is placed on a rough horizontal surface and given a velocity V0 to the right. A is a point on the surface to the left of the block.
(a) Write the angular momentum of the block about point A just after it begins to move
(b) Due to friction the block stops. What happened to its angular momentum about point A? Which torque is responsible for change in angular momentum of the block?

The correct Answer is:(a) MV0b2
(b) Normal reaction produces a torque
Topper's Solved these Questions
Similar Questions
Knowledge Check
A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNoneA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
Aangular momentum about A is mvh initiallyBthe velocity of the block decreases at time passes.Ctorque of the forces acting on block is zero about ADangular momentum is not conserved about A.
A rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
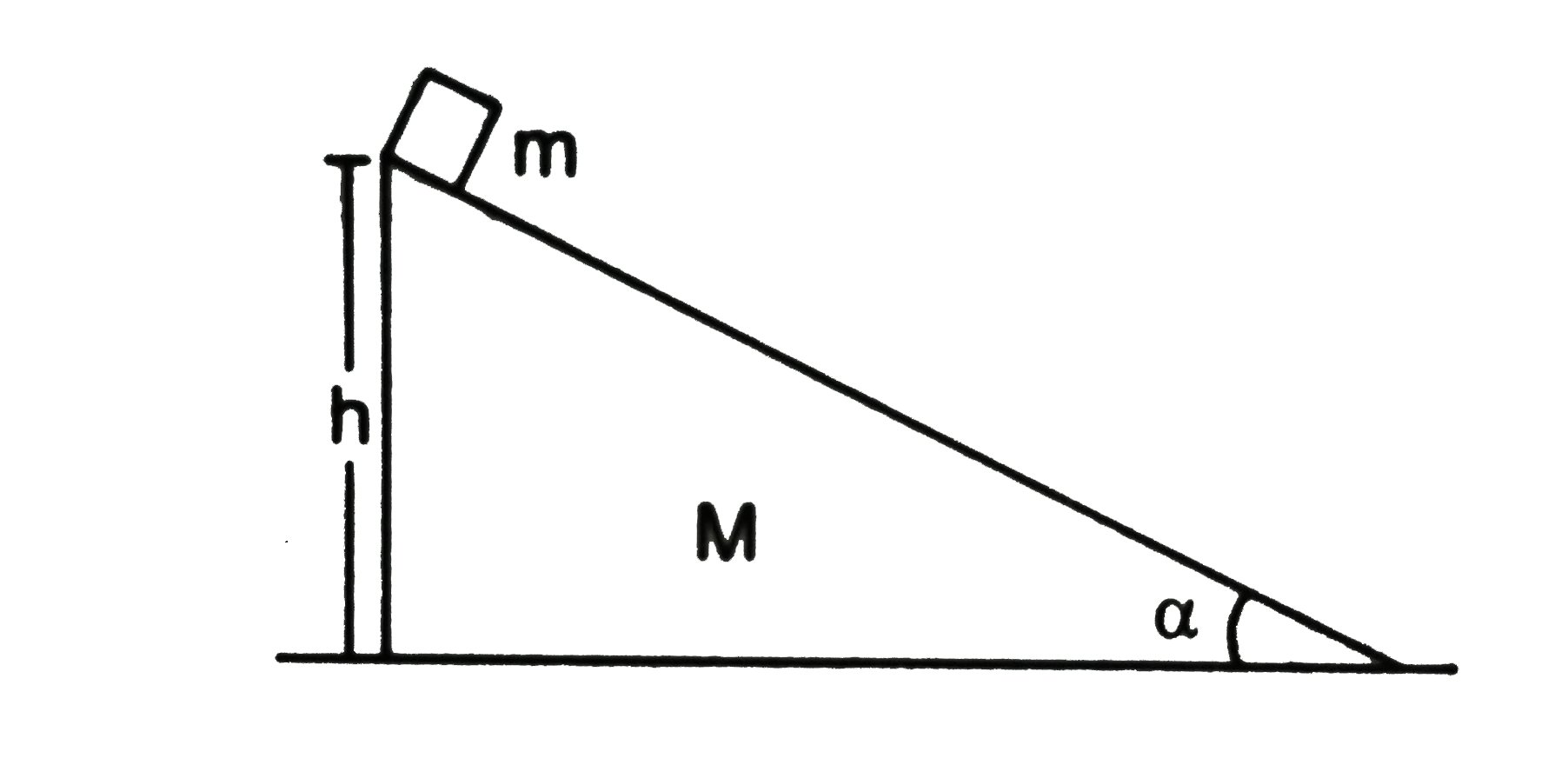
View SolutionA block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
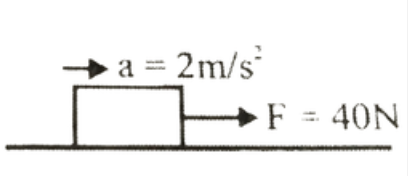
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure

View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution