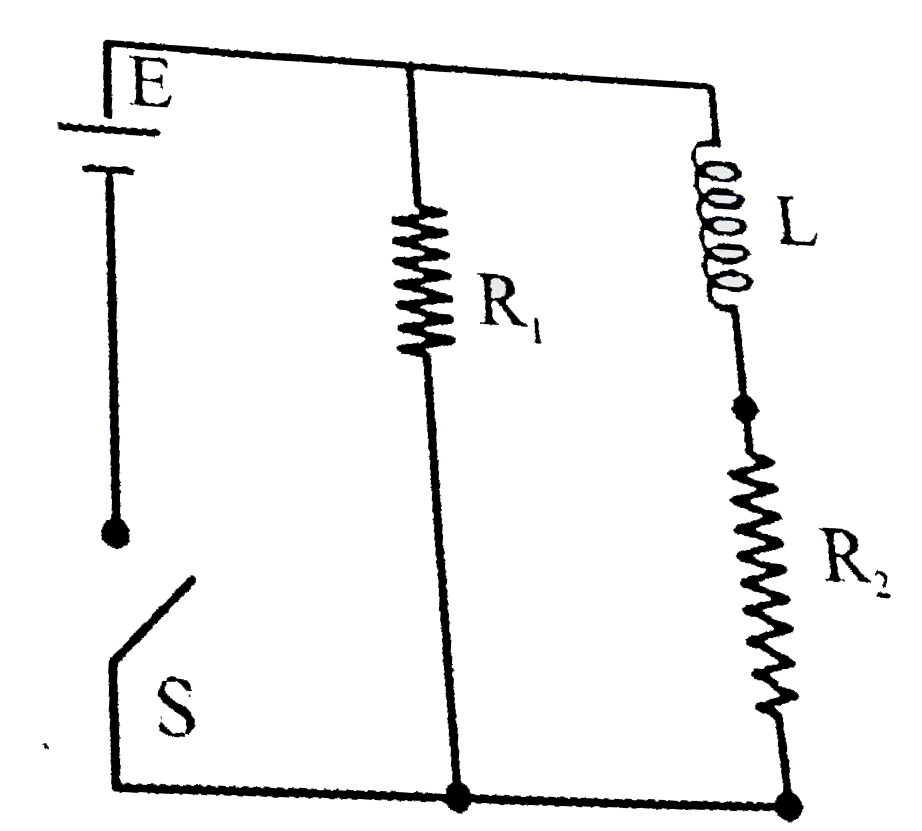
An inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
6e−5tV
12te−3tV
6(1−e−10.2)V
12e−5tV
The correct Answer is:D
E(across BC)=LdI2dt+R2I2 [using Kirchhoff's law]…(i)
I2=I0(I−e−t/t0)

At t = 0, I0=ER2=122=6A
τL=t0=LR=400×10−32Ω=0.2s
∴ I2=6(1−e−t/0.2) [using Eq. (i)]
Potential drop area L = E−R2I2
=12−2×6(1−e−t/0.2)=12e−t/0.2=12e−5tV
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
An inductor of inductance L=400mH and resistors of resistances R1=2Ω and R2=2Ω are connected to a battery of emf E=12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t=0.

What is the potential dro across L s a function of time? After the steady state is reached, the switch is opened. What is the direction ad the magnitude of current throough R1 as a function of time?View SolutionAn inductor of inductance L = 8 H and a resistor of resistance R = 2Ω are connected in series with a battery of emf E = 10 V as shown in the figure. If the switch is closed at t = 0, then the voltage drop across the inductor at t = 1 s will be in volts)
View Solution
Knowledge Check
- Question 1 - Select One
Three resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2 - Question 2 - Select One
Four resistors are connected as shown in the figure. A 6 V battery of negligible resistance is connected across terminal battery of negligible resistance A and C. The potential difference across terminal B and D will be
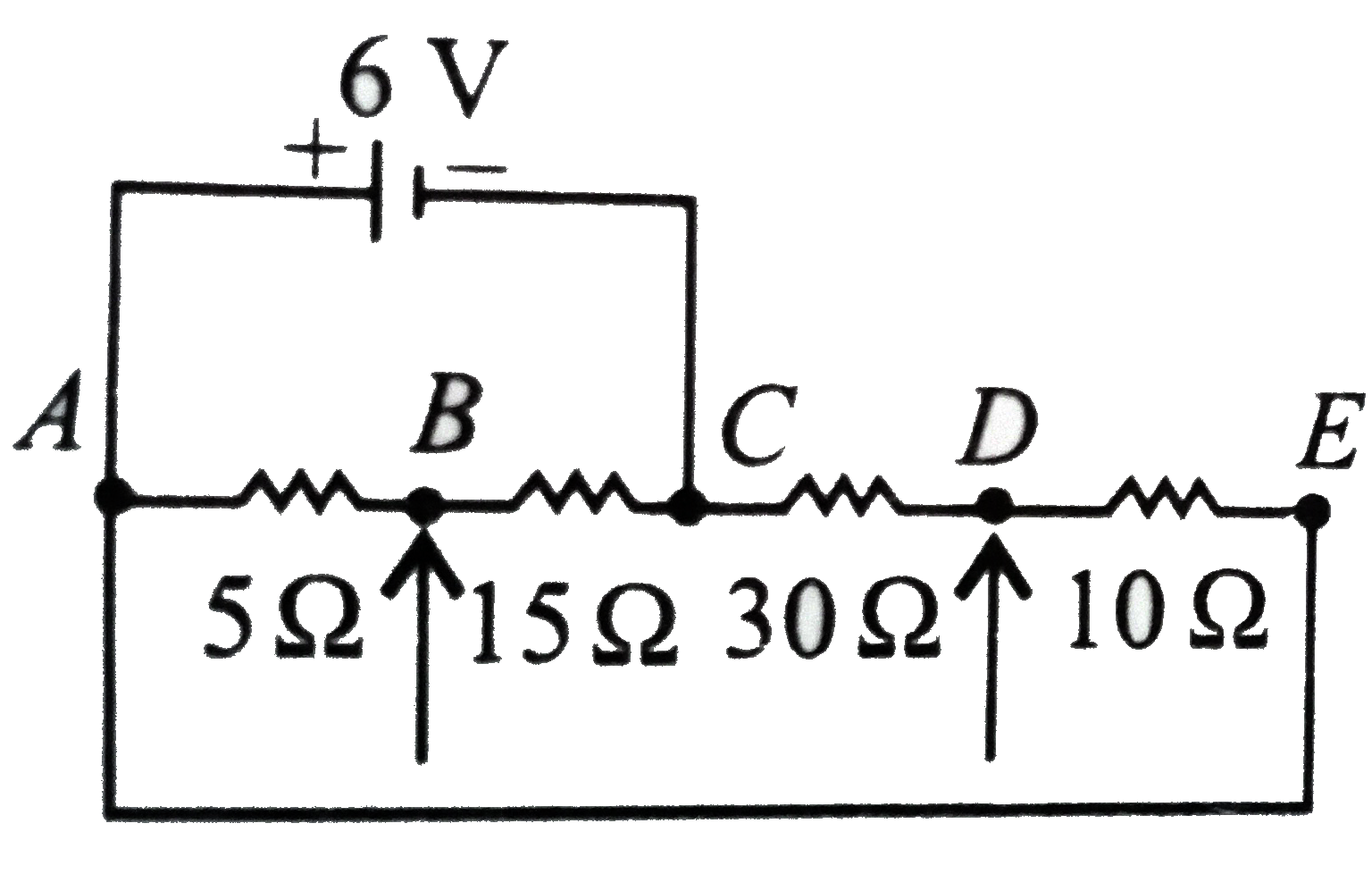 AzeroB1.5VC2VD3V
AzeroB1.5VC2VD3V - Question 3 - Select One
A pure inductor L, a capactior C and a resistance R are connected across a battery of emf E and internal resistance r as shows in Fig. Switch SW is closed at t=0, select the correct altermative (S).
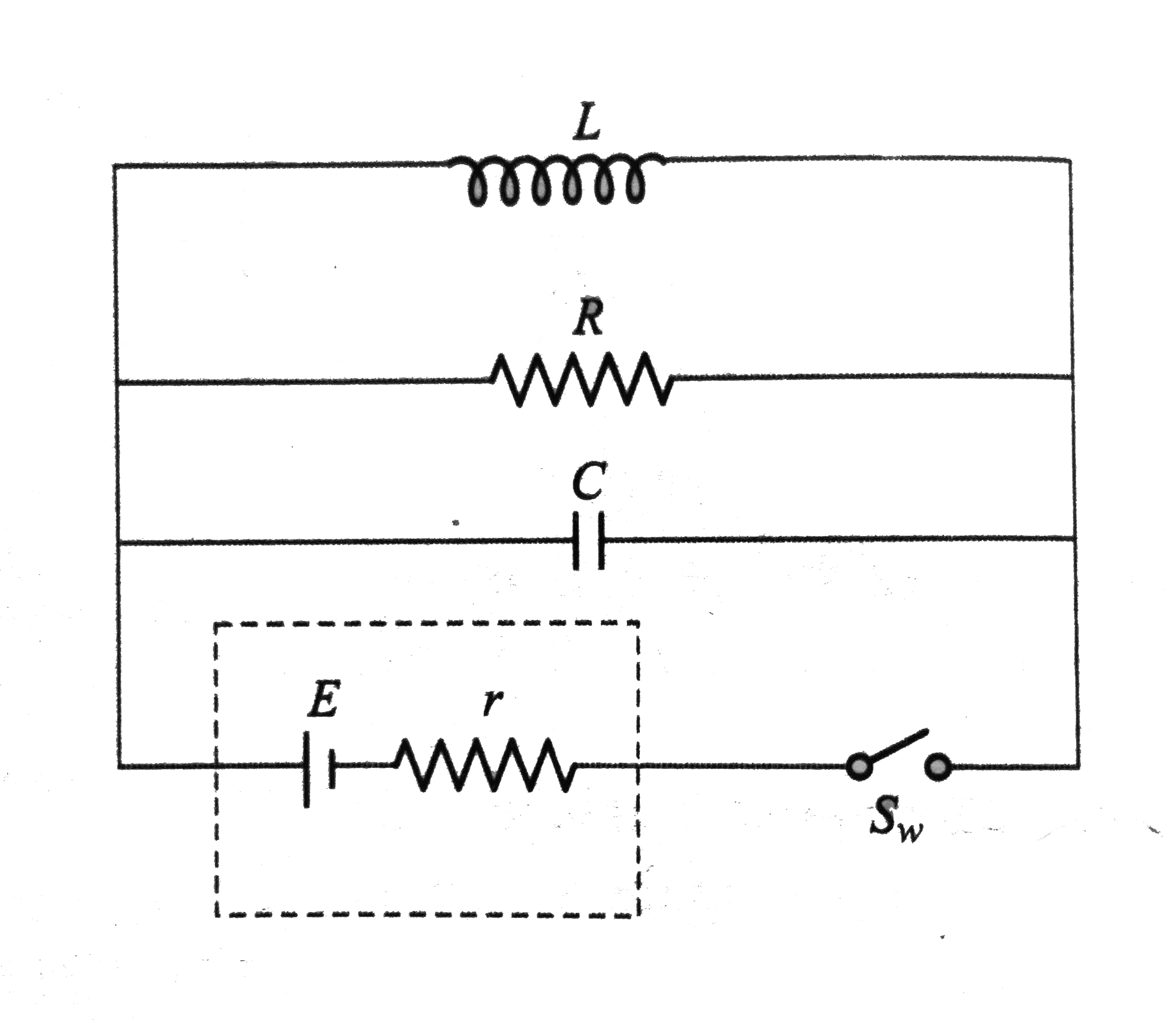 ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
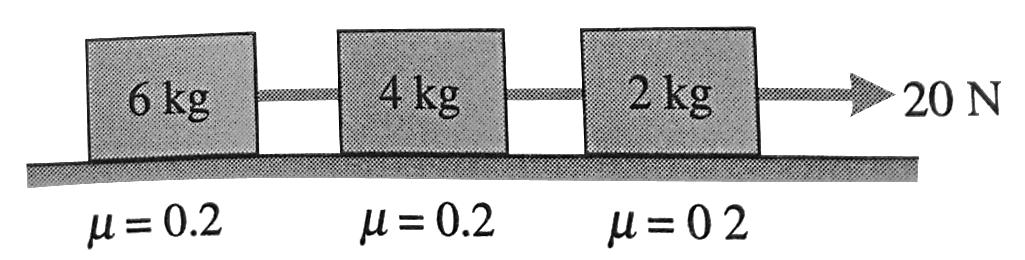
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. Friction force on 6 kg block isView SolutionIn the circuit shown in figure switch S is closed at time t=0
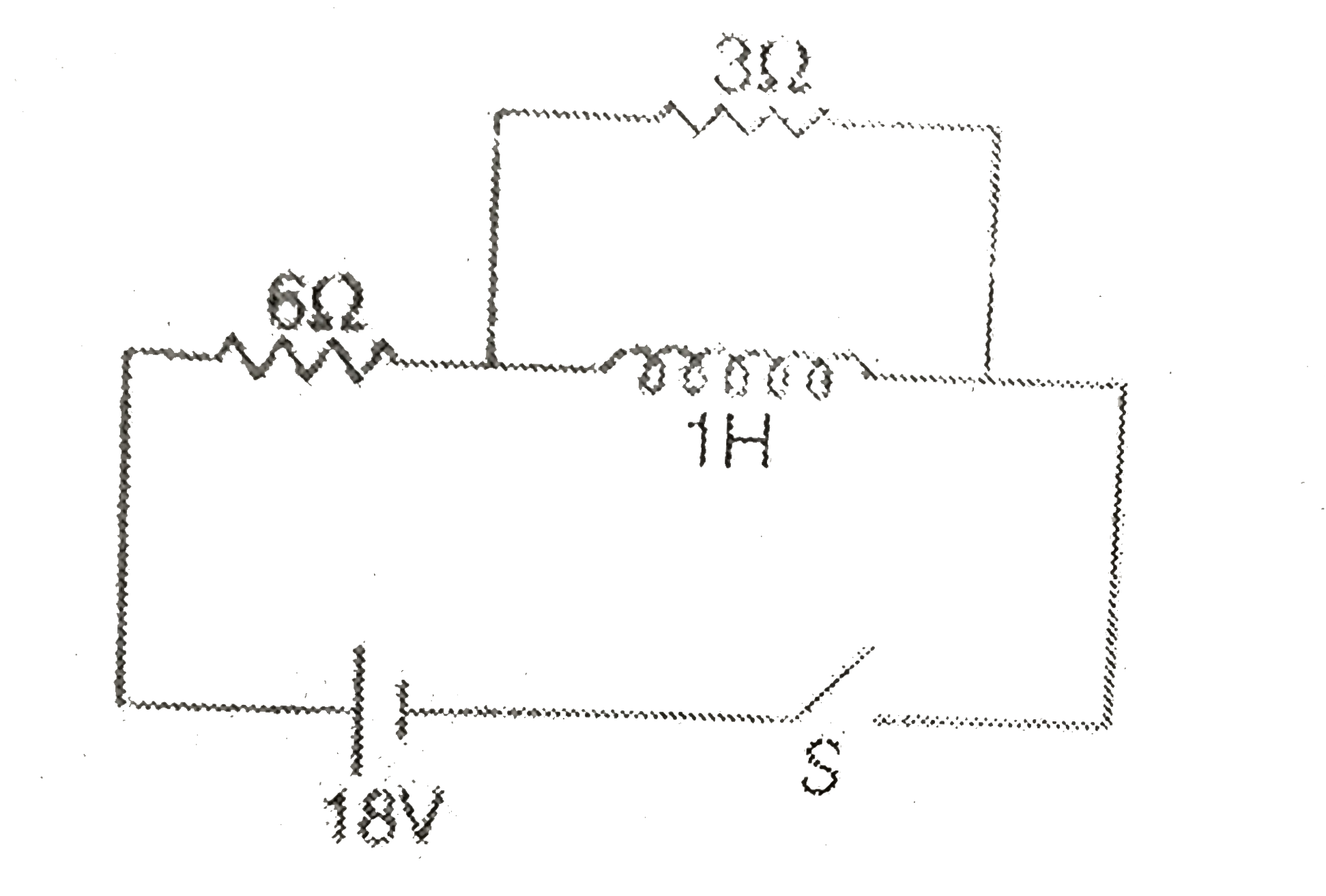
Potential difference across 3Ω resistance at time t is given byView SolutionA battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA circuit containing five resistors is connected to a battery with a 12 v emf as shown in figure. The potential difference across 4Ω resistor is
 View Solution
View Solution

