An optical fibre (RI = 1.72) is surrounded by a glass coating (RI= 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
The correct Answer is:A
μ1sinθc=m2sin90∘
sinθc=1.501.72
→θc=sin−1[7588]

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
Statement I: A ray is incident from outside on a glass sphere surrounded by air as shown in Figure. This ray may suffer total internal reflection at the second interface.

Statement II: For a ray going from a denser to rarer medium, the ray may suffer total internal reflection.
View SolutionThe figure shows the path of a ray passing through an equiangular prism PQR. It is incident on face PR at angle slightly greater than the critical angle for total internal reflection . If the angle α shown in the figure is 30∘ . Calculate the R.I. of the material of the prism.
_E01_145_Q01.png)
View Solution
Knowledge Check
Assertion : Optical fibres make use of total internal reflection.
Reason : Light undergoes successive total internal reflections as it moves through an optical fibre.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
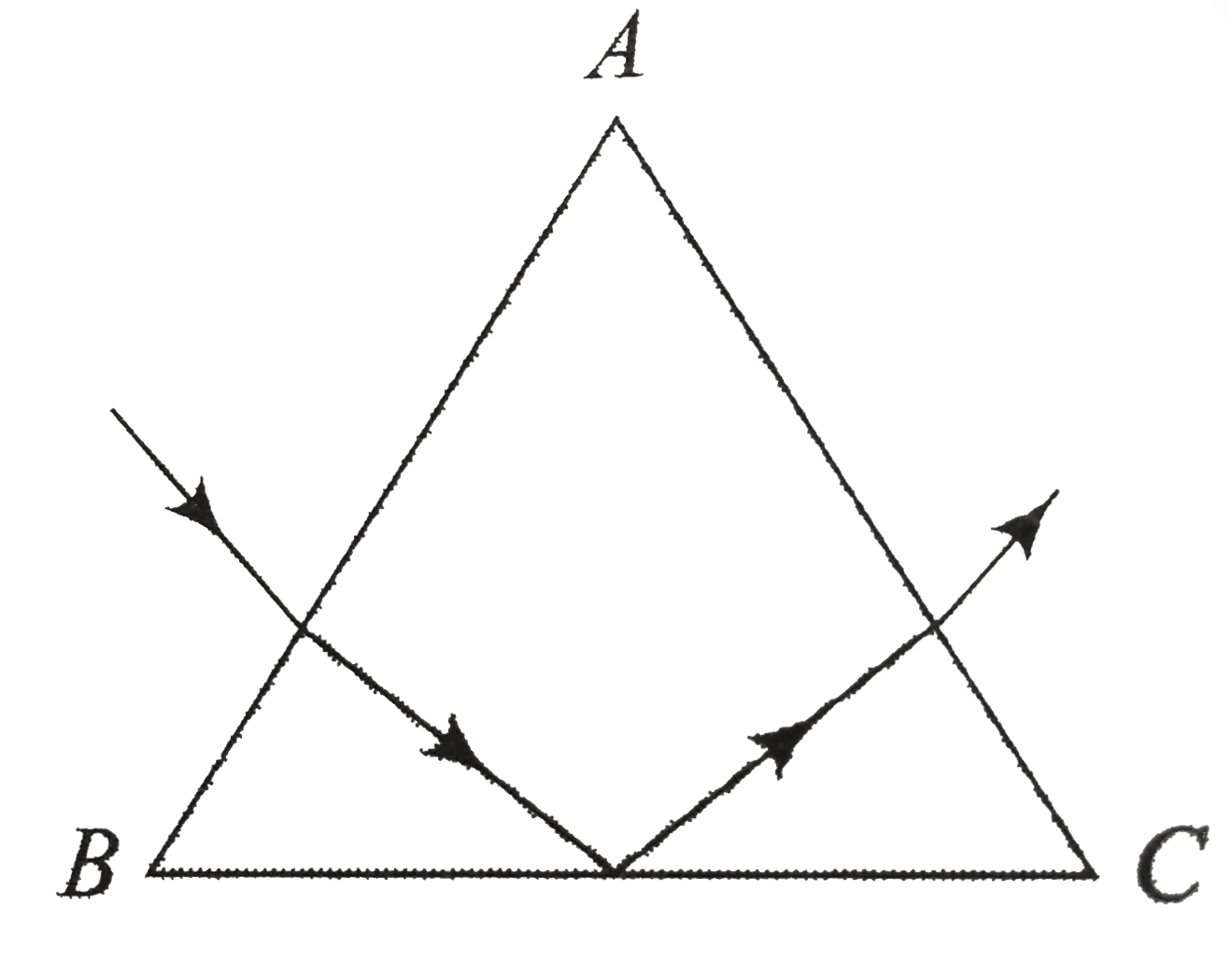
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

View SolutionFor a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.

View SolutionIf refractive index of glass is 1.50 and of water is 1.33, then criticle angle is
View SolutionInside a solid glass sphere of radius R, a point source of light lies at a distance x(x<R) from centre of the sphere. The solid is surrounded by air of refractive index 1. The maximum angle of incidence for rays incident on the spherical glass air interface directly from the point soure is:
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by

View Solution
