Find the minimum number of cell required to produce an electron current of 1.5A through a resistance of 30Ω .Given that the emf internal resistance of each cell are 1.5V and 1.0Ω respectively
To solve the problem of finding the minimum number of cells required to produce an electron current of 1.5 A through a resistance of 30 Ω, given that the emf of each cell is 1.5 V and the internal resistance is 1.0 Ω, we can follow these steps:
1. Identify the Given Values:
- Current (I) = 1.5 A
- Resistance (R) = 30 Ω
- Emf of each cell (E) = 1.5 V
- Internal resistance of each cell (r) = 1.0 Ω
2. Calculate the Total Resistance Required:
The total resistance (R_total) in the circuit can be calculated using Ohm's law:
V=I×R
Here, V is the total voltage supplied by the cells. Rearranging gives:
V=1.5A×30Ω=45V
3. Set Up the Equation for Total Voltage:
The total voltage (V) provided by n cells in series is:
V=n×E
Therefore, we have:
n×1.5V=45V
Solving for n gives:
n=45V1.5V=30
4. Calculate the Total Internal Resistance:
The total internal resistance (R_internal) for n cells in series is:
Rinternal=n×r=n×1.0Ω=nΩ
Therefore, for n = 30:
Rinternal=30Ω
5. Calculate the Total Resistance in the Circuit:
The total resistance in the circuit (R_total) is the sum of the external resistance and the internal resistance:
Rtotal=R+Rinternal=30Ω+30Ω=60Ω
6. Check the Current with the Total Resistance:
Using Ohm's law again to find the current with the total resistance:
I=VRtotal
The total voltage from the cells is:
V=n×E=30×1.5V=45V
Therefore:
I=45V60Ω=0.75A
Since this is not equal to the required current of 1.5 A, we need to adjust our calculations.
7. Re-evaluate the Configuration:
Since we need to achieve a current of 1.5 A, we can consider using cells in parallel. The effective internal resistance when cells are in parallel is given by:
Reffective=rn
The total resistance in the circuit will then be:
Rtotal=R+Reffective=30Ω+1.0Ωn
8. Set Up the Current Equation:
The current through the circuit can be expressed as:
I=EnetRtotal
Where Enet=n×E. Thus:
I=n×1.530+1.0n
Setting this equal to 1.5 A:
1.5=1.5n30+1.0n
9. Solve for n:
Cross-multiplying and simplifying gives:
1.5(30+1.0n)=1.5n
This leads to:
45+1.5n=1.5n
Rearranging gives:
1.5n2−1.5n−45=0
Dividing through by 1.5:
n2−n−30=0
Factoring gives:
(n−6)(n+5)=0
Thus, n=6 (since n cannot be negative).
Final Answer:
The minimum number of cells required is 6.
- Current (I) = 1.5 A
- Resistance (R) = 30 Ω
- Emf of each cell (E) = 1.5 V
- Internal resistance of each cell (r) = 1.0 Ω
The total resistance (R_total) in the circuit can be calculated using Ohm's law:
V=I×R
Here, V is the total voltage supplied by the cells. Rearranging gives:
V=1.5A×30Ω=45V
The total voltage (V) provided by n cells in series is:
V=n×E
Therefore, we have:
n×1.5V=45V
Solving for n gives:
n=45V1.5V=30
The total internal resistance (R_internal) for n cells in series is:
Rinternal=n×r=n×1.0Ω=nΩ
Therefore, for n = 30:
Rinternal=30Ω
The total resistance in the circuit (R_total) is the sum of the external resistance and the internal resistance:
Rtotal=R+Rinternal=30Ω+30Ω=60Ω
Using Ohm's law again to find the current with the total resistance:
I=VRtotal
The total voltage from the cells is:
V=n×E=30×1.5V=45V
Therefore:
I=45V60Ω=0.75A
Since this is not equal to the required current of 1.5 A, we need to adjust our calculations.
Since we need to achieve a current of 1.5 A, we can consider using cells in parallel. The effective internal resistance when cells are in parallel is given by:
Reffective=rn
The total resistance in the circuit will then be:
Rtotal=R+Reffective=30Ω+1.0Ωn
The current through the circuit can be expressed as:
I=EnetRtotal
Where Enet=n×E. Thus:
I=n×1.530+1.0n
Setting this equal to 1.5 A:
1.5=1.5n30+1.0n
Cross-multiplying and simplifying gives:
1.5(30+1.0n)=1.5n
This leads to:
45+1.5n=1.5n
Rearranging gives:
1.5n2−1.5n−45=0
Dividing through by 1.5:
n2−n−30=0
Factoring gives:
(n−6)(n+5)=0
Thus, n=6 (since n cannot be negative).
The minimum number of cells required is 6.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionFor the given circuit,
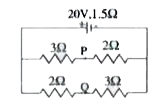
If internal resistance of cell is 1.5Ω, then
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionCurrent passing through 1Ω resistance is zero. Then the emf E is
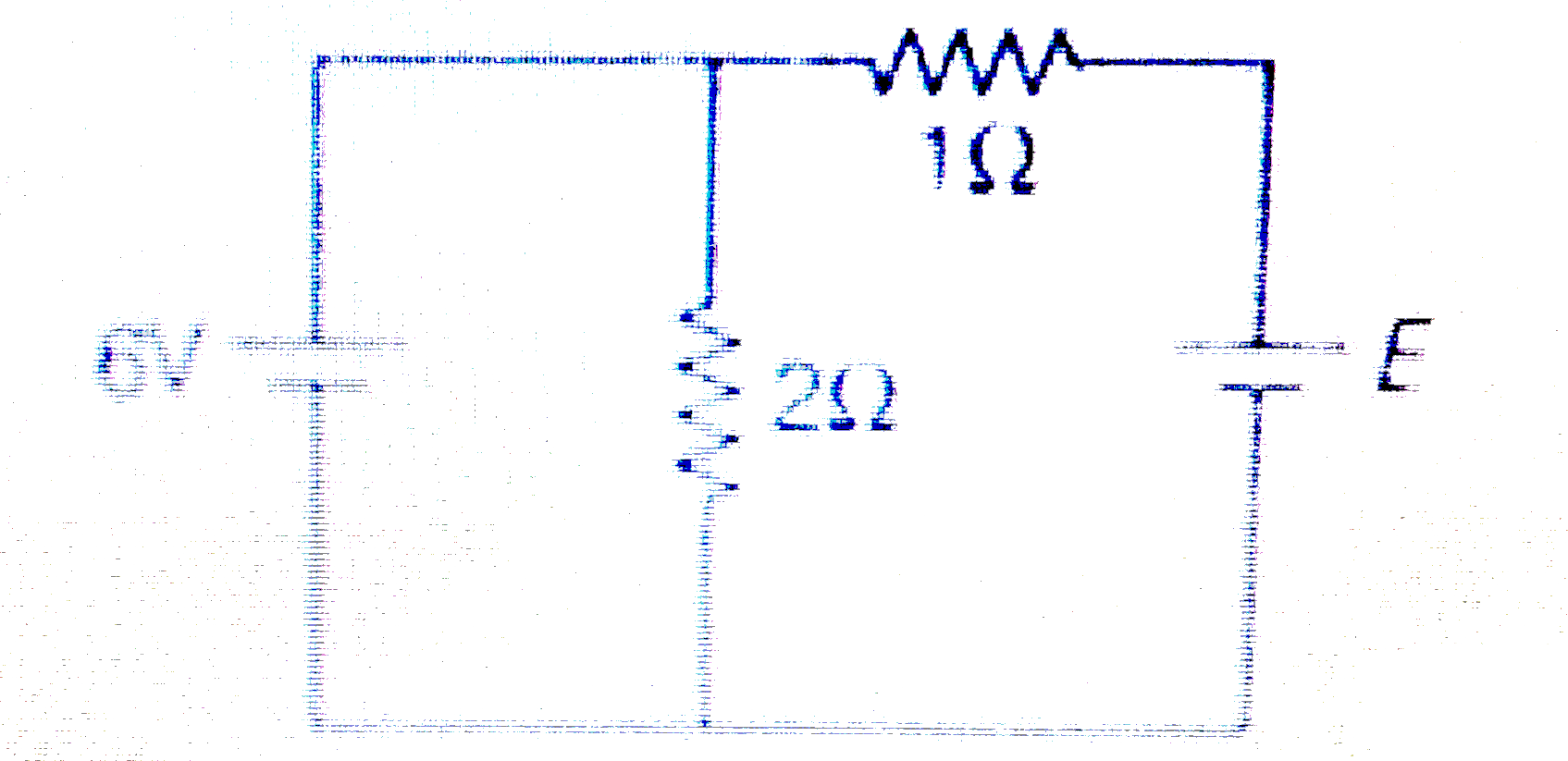
View SolutionThe resistance of the four arms A, B, C and D of a wheatstone bridge as shown in the figure are 10Ω, 20Ω ,30Ω and 60Ω respectively . The emf and internal resistance of the cell are 15V and 2.5Ω respectively . If the galvanometer resistance is 80Ω then the net current drawn from the cell will be
_PHY_E05_111_Q01.png)
View SolutionFor the given circuit, if internal resistance of cell is 1.5Ω thenVp−Vq is equal to:
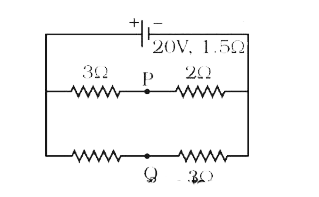
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View SolutionA battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solution
