If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
1.1MPa
0.11MPa
0.101MPa
0.011MPa
The correct Answer is:B
To solve the problem, we need to determine the water pressure at the bottom of the container when it is subjected to both horizontal and vertical accelerations.
1. Understand the Effective Gravity:
The effective gravity (geff) in a liquid when the container is accelerated both horizontally and vertically can be calculated using vector addition. The horizontal acceleration is g2 and the vertical acceleration is also g2.
\(
g_{eff} = \sqrt{(g/2)^2 + (g/2)^2} = \sqrt{(g^2/4) + (g^2/4)} = \sqrt{(g^2/2)} = \frac{g}{\sqrt{2}}
\)
2. Calculate the Depth of the Liquid:
The container is half-filled with liquid. Given the height of the container is 2m, the depth of the liquid (h) is:
\(
h = \frac{2}{2} = 1 \text{ m}
\)
3. Calculate the Pressure at the Bottom:
The pressure at the bottom of the container due to the liquid is given by the hydrostatic pressure formula:
\(
P = P_{atm} + \rho g_{eff} h
\)
where:
- \( P_{atm} = 10^5 \, \text{N/m}^2 \) (atmospheric pressure)
- \( \rho = 1000 \, \text{kg/m}^3 \) (density of water)
- \( g_{eff} = \frac{g}{\sqrt{2}} = \frac{10}{\sqrt{2}} \, \text{m/s}^2 \)
- \( h = 1 \, \text{m} \)
Substituting the values:
\(
P = 10^5 + 1000 \cdot \left(\frac{10}{\sqrt{2}}\right) \cdot 1
\)
\(
P = 10^5 + 1000 \cdot \frac{10}{\sqrt{2}} = 10^5 + \frac{10000}{\sqrt{2}} \approx 10^5 + 7071.07
\)
\(
P \approx 10^5 + 7071.07 \approx 107071.07 \, \text{N/m}^2
\)
4. Final Answer:
The water pressure at the bottom of the center of the box is approximately:
\(
P \approx 107071.07 \, \text{N/m}^2
\)
The effective gravity (geff) in a liquid when the container is accelerated both horizontally and vertically can be calculated using vector addition. The horizontal acceleration is g2 and the vertical acceleration is also g2.
g_{eff} = \sqrt{(g/2)^2 + (g/2)^2} = \sqrt{(g^2/4) + (g^2/4)} = \sqrt{(g^2/2)} = \frac{g}{\sqrt{2}}
\)
The container is half-filled with liquid. Given the height of the container is 2m, the depth of the liquid (h) is:
h = \frac{2}{2} = 1 \text{ m}
\)
The pressure at the bottom of the container due to the liquid is given by the hydrostatic pressure formula:
P = P_{atm} + \rho g_{eff} h
\)
- \( P_{atm} = 10^5 \, \text{N/m}^2 \) (atmospheric pressure)
- \( \rho = 1000 \, \text{kg/m}^3 \) (density of water)
- \( g_{eff} = \frac{g}{\sqrt{2}} = \frac{10}{\sqrt{2}} \, \text{m/s}^2 \)
- \( h = 1 \, \text{m} \)
P = 10^5 + 1000 \cdot \left(\frac{10}{\sqrt{2}}\right) \cdot 1
\)
P = 10^5 + 1000 \cdot \frac{10}{\sqrt{2}} = 10^5 + \frac{10000}{\sqrt{2}} \approx 10^5 + 7071.07
\)
P \approx 10^5 + 7071.07 \approx 107071.07 \, \text{N/m}^2
\)
The water pressure at the bottom of the center of the box is approximately:
P \approx 107071.07 \, \text{N/m}^2
\)
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:True/False
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:SCQ_TYPE
Explore 13 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Length of exposed portion of top of box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
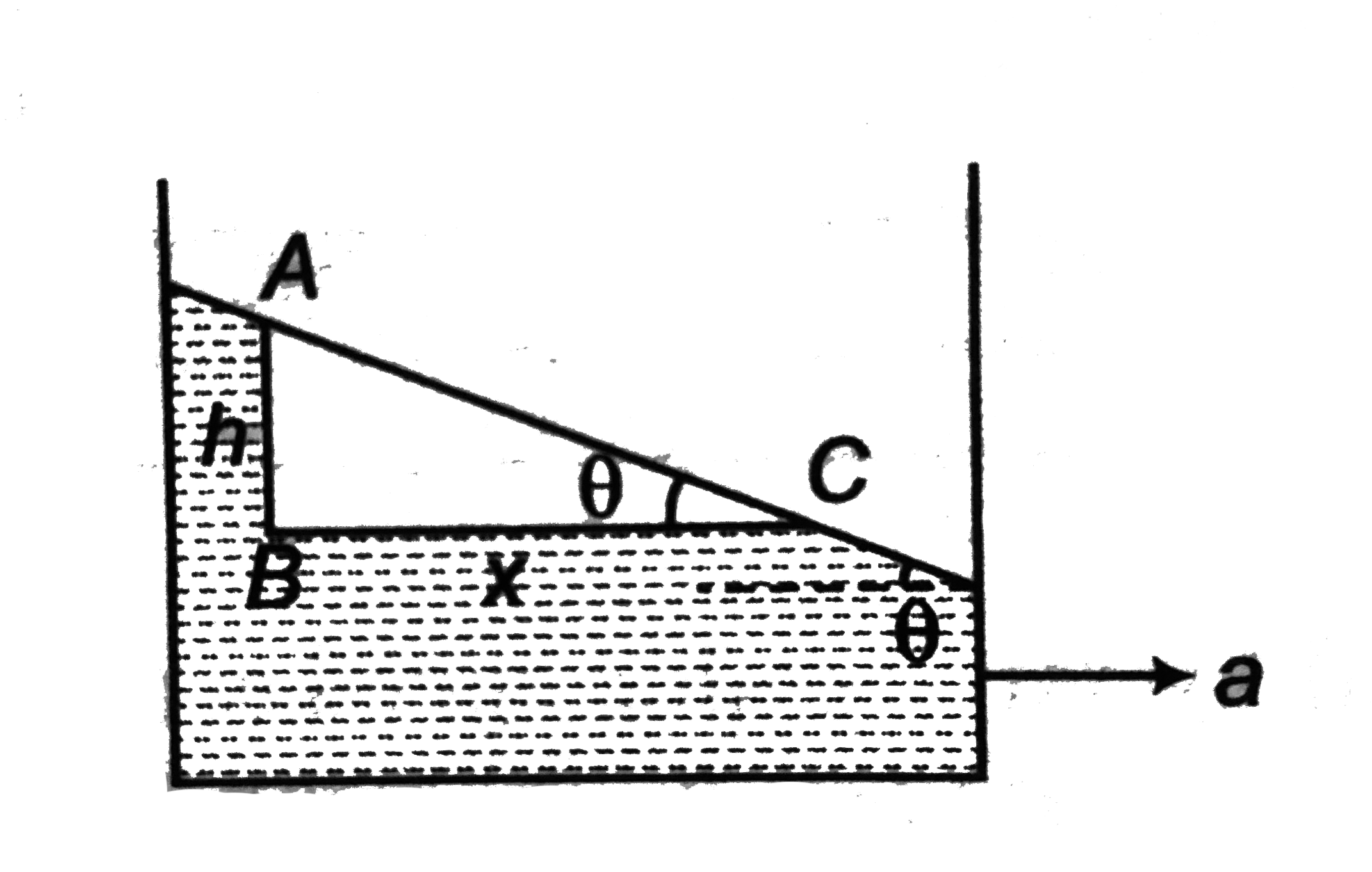
Using the pressure equation along the path ABC find the angle θ.
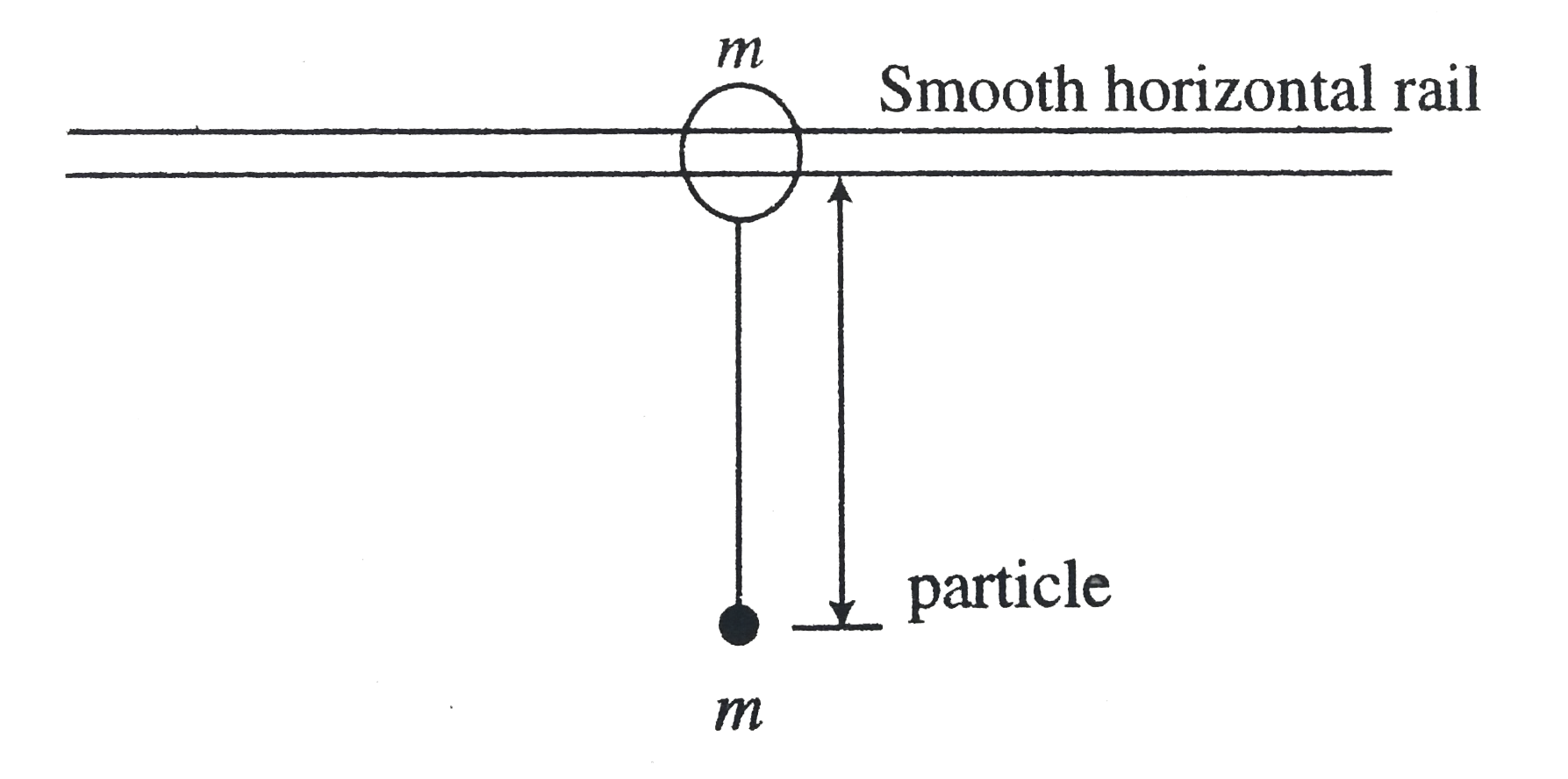
View SolutionThe ring shown in fig. is given a constant horizontal acceleration (a0=g√3). The maximum deflection of the string from the vertical is θ0. Then
View SolutionThe minimum horizontal acceleration of the container4 so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
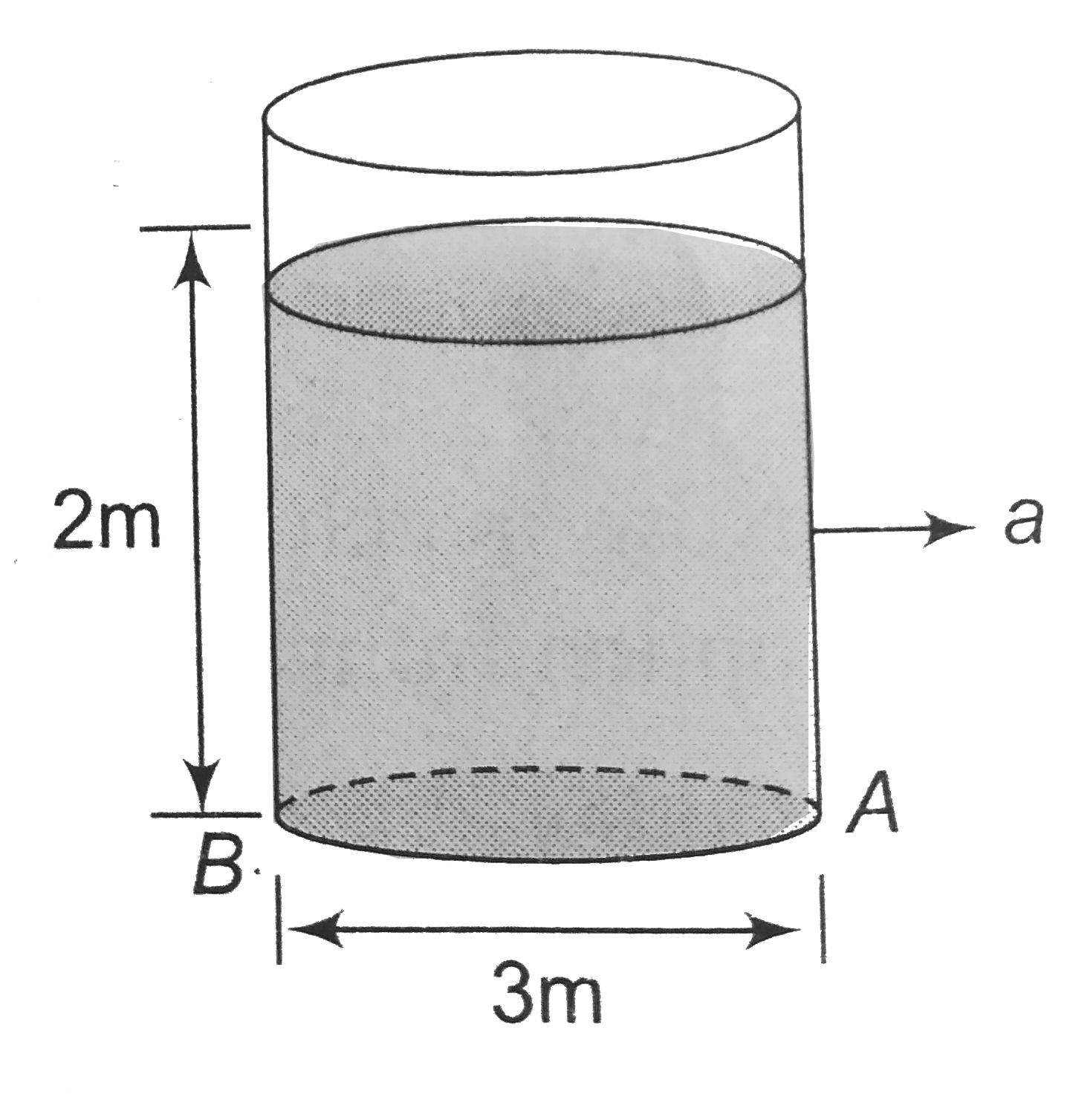
View SolutionThe minimum horizontal acceleration of the container a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)

View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View SolutionFigure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.

View Solution