In a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2 π r v s − 1 around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g = 10 m s − 1 )
tan−1(58)
tan−1(35)
cos−1(35)
cos−1(58)
The correct Answer is:D
To solve the problem of finding the angle of inclination of the string with the vertical in a conical pendulum arrangement, we will follow these steps:
Step 1: Understand the Problem
We have a conical pendulum with:
- Length of the string (L) = 1 m
- Mass of the bob (m) = 100 g = 0.1 kg (conversion to kg)
- Number of revolutions per second (n) = 2π r/s = 2/5 revolutions per second
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Identify Forces Acting on the Bob
The forces acting on the bob are:
1. The gravitational force (mg) acting downwards.
2. The tension (T) in the string acting along the string.
Step 3: Resolve the Tension into Components
The tension can be resolved into two components:
- Vertical component: Tcosθ (balances the weight)
- Horizontal component: Tsinθ (provides the centripetal force)
Step 4: Write the Equations of Motion
1. For vertical motion (balancing forces):
Tcosθ=mg
2. For horizontal motion (centripetal force):
Tsinθ=mv2r
where v is the linear velocity and r is the radius of the circular path.
Step 5: Express Linear Velocity in Terms of Angular Velocity
The linear velocity v can be expressed in terms of angular velocity ω:
v=rω
Given n=25 revolutions per second, we can find ω:
ω=2πn=2π(25)=4π5 rad/s
Step 6: Substitute for v and r
The radius r can be expressed in terms of L and θ:
r=Lsinθ=1⋅sinθ=sinθ
Thus, the centripetal force equation becomes:
Tsinθ=m(rω)2r=mrω2
Substituting r=sinθ gives:
Tsinθ=msinθ(4π5)2
Step 7: Simplify the Equations
From the vertical force equation:
T=mgcosθ
Substituting this into the horizontal force equation:
mgcosθsinθ=msinθ(4π5)2
Cancelling msinθ (assuming sinθ≠0):
gcosθ=(4π5)2
Step 8: Solve for cosθ
Rearranging gives:
cosθ=g(4π5)2
Substituting g=10:
cosθ=10(16π225)=25016π2
Step 9: Calculate θ
Now, we can find θ:
θ=cos−1(25016π2)
Step 10: Final Calculation
Using π≈3.14:
θ≈cos−1(25016⋅(3.14)2)
Calculating this gives the angle of inclination.
We have a conical pendulum with:
- Length of the string (L) = 1 m
- Mass of the bob (m) = 100 g = 0.1 kg (conversion to kg)
- Number of revolutions per second (n) = 2π r/s = 2/5 revolutions per second
- Acceleration due to gravity (g) = 10 m/s²
The forces acting on the bob are:
1. The gravitational force (mg) acting downwards.
2. The tension (T) in the string acting along the string.
The tension can be resolved into two components:
- Vertical component: Tcosθ (balances the weight)
- Horizontal component: Tsinθ (provides the centripetal force)
1. For vertical motion (balancing forces):
Tcosθ=mg
2. For horizontal motion (centripetal force):
Tsinθ=mv2r
where v is the linear velocity and r is the radius of the circular path.
The linear velocity v can be expressed in terms of angular velocity ω:
v=rω
Given n=25 revolutions per second, we can find ω:
ω=2πn=2π(25)=4π5 rad/s
The radius r can be expressed in terms of L and θ:
r=Lsinθ=1⋅sinθ=sinθ
Thus, the centripetal force equation becomes:
Tsinθ=m(rω)2r=mrω2
Substituting r=sinθ gives:
Tsinθ=msinθ(4π5)2
From the vertical force equation:
T=mgcosθ
Substituting this into the horizontal force equation:
mgcosθsinθ=msinθ(4π5)2
Cancelling msinθ (assuming sinθ≠0):
gcosθ=(4π5)2
Rearranging gives:
cosθ=g(4π5)2
Substituting g=10:
cosθ=10(16π225)=25016π2
Now, we can find θ:
θ=cos−1(25016π2)
Using π≈3.14:
θ≈cos−1(25016⋅(3.14)2)
Calculating this gives the angle of inclination.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason
28 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
In a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2πmvs−1around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is

View SolutionOne end of a string of length 1 m is tied to a body of mass 0.5 kg. It is whirled in a vertical circle with angular velocity 4 rad s−1. Find the tension in the string when the body is at the lower most point of its motion. (take, g = 10 ms−1)
View SolutionA massless, inextensible string of length 1 m has a breaking strength of 1 kg wt. A stone of mass 0.2 kg tied to one end of the string is made to move in a vertical circle. Can the stone describe the vertical circle? (g=10ms−2)
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
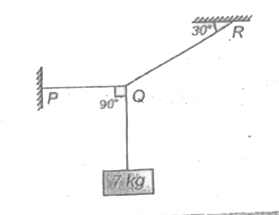
View SolutionA stone of mass 1 kg tied to a string 4 m long and is rotated at constant speed of 40 m/s a vertical circle. The ratio of the tension at the top and the bottom, is (g=10 m/s2)
View SolutionA heavy particle of mass 0.50 kg is hanging from a string fixed with the roof. Find the force exerted by the string on the particle. Take g=9.8ms2
 .
.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
