In a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

1
2
>1
<1
The correct Answer is:A
The two streams strike at the same point on the ground. 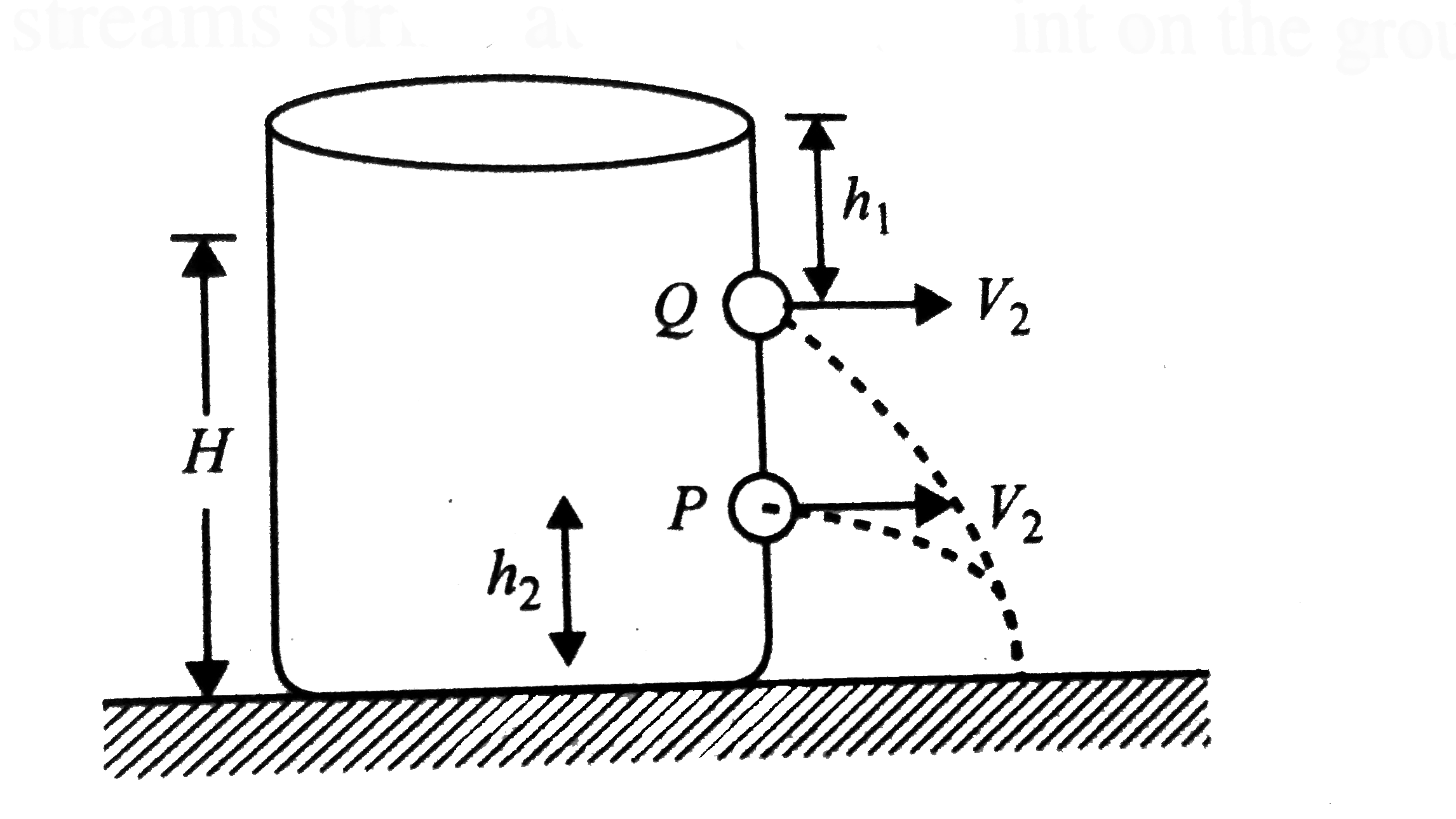
R1=R2=R
u1t1=u2t2………i
Where u1= velocity of efflux at Q=√(2gh1) and u2= velocity of efflux at P=√[2g(H−h2)]
t1=time of fall of water stream through Q is
=√2(H−h1)g
t2= time of fall of the water stream through P=√2h2g
Putting these values is eqn i we get
(H−h1)h1=(H−h1)h2
or [H−(h1+h2)][h1−h2]=0
H=h1+h2 is irrelevant because the holes are at two different heights. Therefore h1=h2 or h1h2=1
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View Solution
Knowledge Check
A large open tank has two holes in the wall. One is square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth of 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then R is equal to
AL/√(2π)B2πLCLDL/2πA tank full of water has a small hole at the bottom. If one-fourth of the tank is emptied in t1 seconds and the remaining three-fourths of the tank is emptied in t2 seconds. Then the ratio t1t2 is
A√3B√2C2−√2√2D2−√3√3The pressure P1 at the top of a dam and P2 at a depth h from the top inside water (density ρ) are related as :
AP1>P2BP1=P2CP1−P2=hρgDP2−P1=hρg
A rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
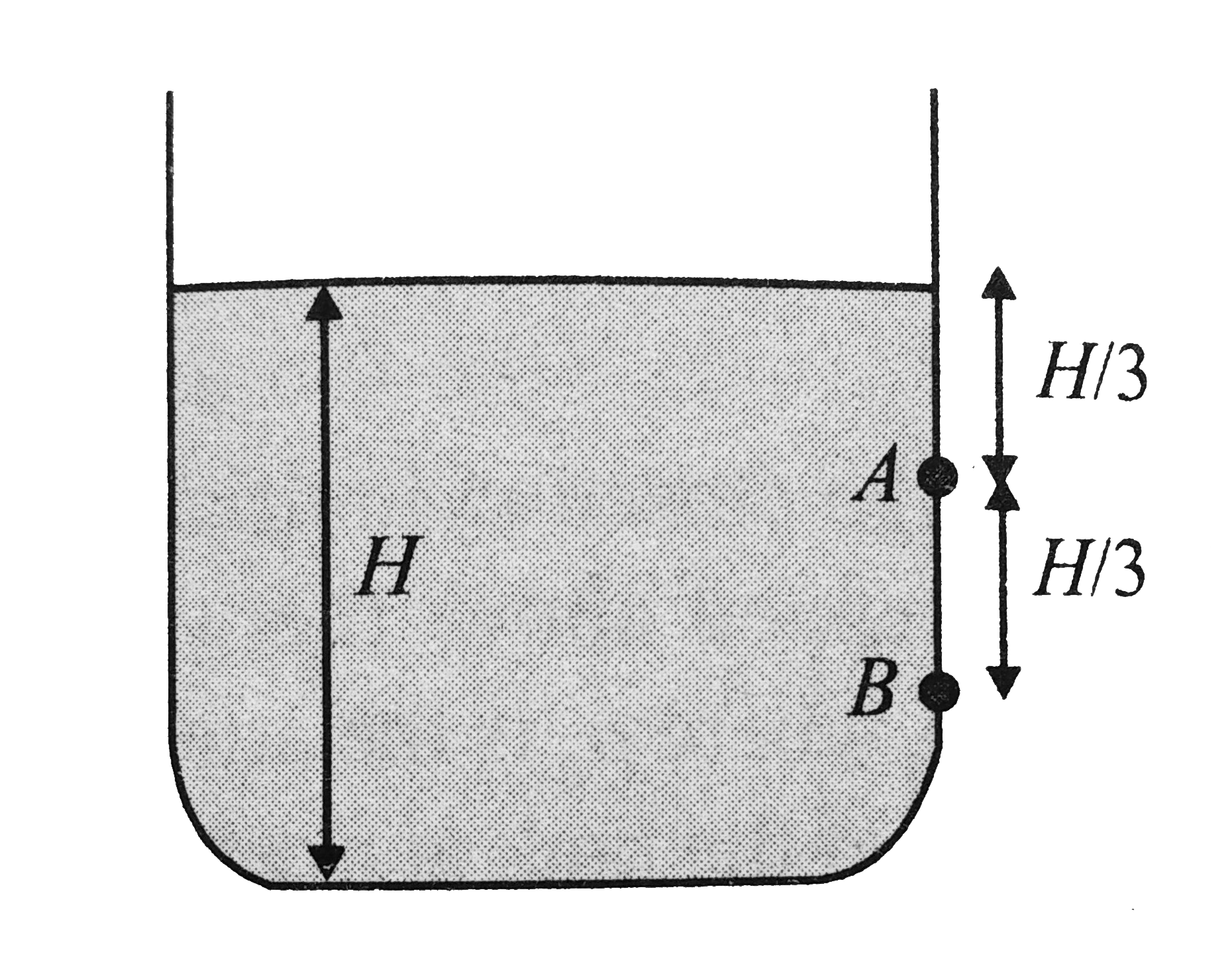
View SolutionThe area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x

View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View Solution
