In the previous problem, if O is the point on AD and is the perpendicular from the centre of the circle, will be
depands upon and charge
The correct Answer is:A
To solve the problem step by step, let's analyze the information given and apply the principles of geometry and physics as discussed in the video transcript.
1. Understanding the Setup:
- We have a point O on line AD.
- There is a perpendicular line drawn from the center of the circle (point O1) to point O, denoted as OO1.
- We need to find the ratio OA/OD.
2. Identifying the Triangles:
- The problem mentions two triangles: triangle OOO1 (formed by points O, O1, and the center of the circle) and triangle AOO1 (formed by points A, O, and O1).
- Since OO1 is perpendicular to AD, both triangles share the common side OO1.
3. Congruent Triangles:
- The triangles OOO1 and AOO1 are congruent. This can be established because:
- They share the side OO1.
- The angles at O (angle AOO1 and angle OOO1) are equal (both are right angles).
- The angles at O1 are also equal since they are subtended by the same line (the radius of the circle).
- By the criteria of congruence (Angle-Side-Angle), we conclude that these triangles are congruent.
4. Establishing the Ratio:
- Since the triangles are congruent, the corresponding sides are equal. Therefore:
- OA = OD
- This leads us to conclude that the ratio of OA to OD is:
OAOD=1
5. Final Answer:
- Thus, the final answer for the ratio OA/OD is:
1
- We have a point O on line AD.
- There is a perpendicular line drawn from the center of the circle (point O1) to point O, denoted as OO1.
- We need to find the ratio OA/OD.
- The problem mentions two triangles: triangle OOO1 (formed by points O, O1, and the center of the circle) and triangle AOO1 (formed by points A, O, and O1).
- Since OO1 is perpendicular to AD, both triangles share the common side OO1.
- The triangles OOO1 and AOO1 are congruent. This can be established because:
- They share the side OO1.
- The angles at O (angle AOO1 and angle OOO1) are equal (both are right angles).
- The angles at O1 are also equal since they are subtended by the same line (the radius of the circle).
- By the criteria of congruence (Angle-Side-Angle), we conclude that these triangles are congruent.
- Since the triangles are congruent, the corresponding sides are equal. Therefore:
- OA = OD
- This leads us to conclude that the ratio of OA to OD is:
OAOD=1
- Thus, the final answer for the ratio OA/OD is:
1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
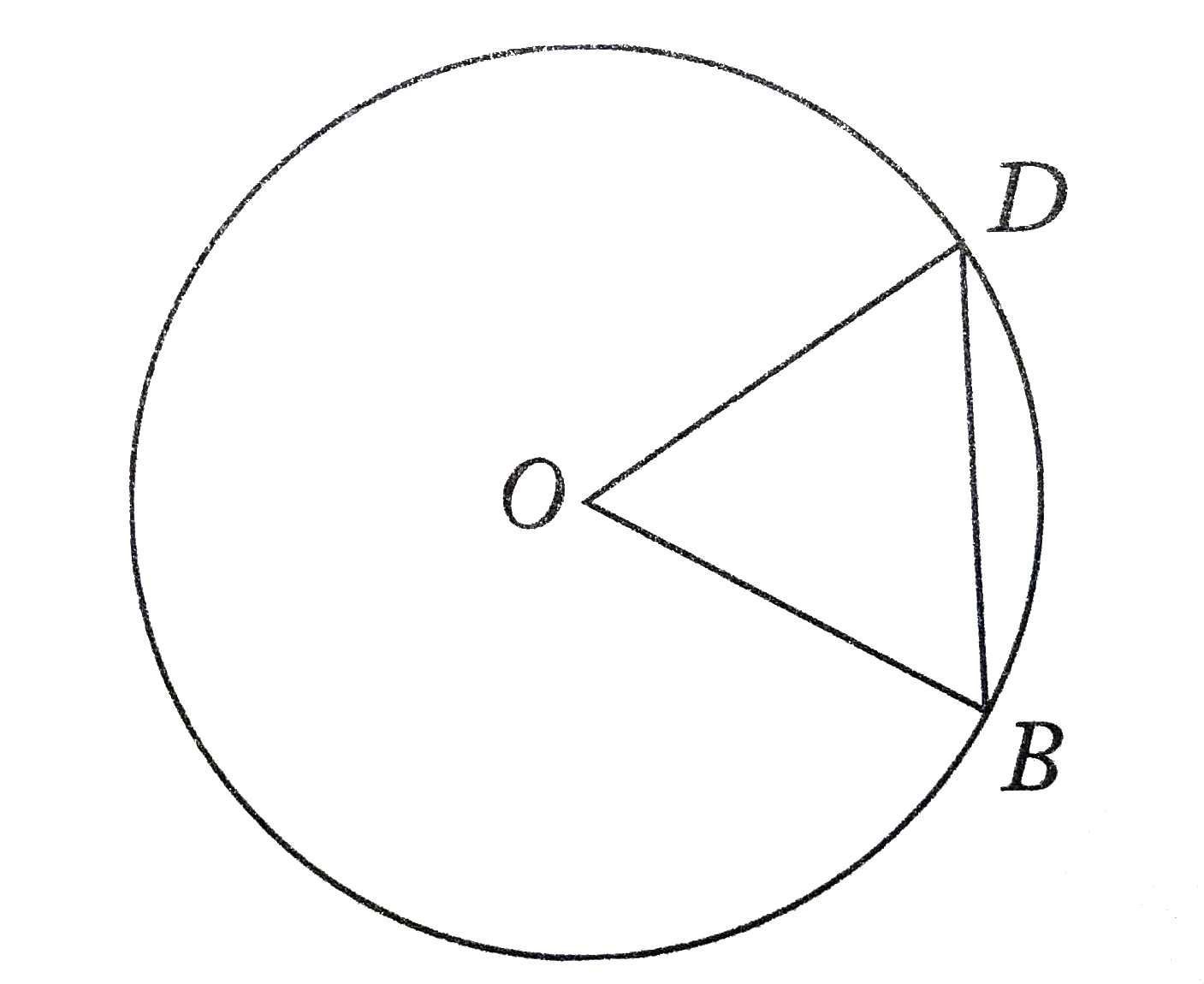
In the circle with center O, OD=BD and arc DB=2π. What is the area of the circle?A36πB16πC12πD4π
Find the coordinates of the foot o the perpendicular from the point (-1, 3) to the line 3x−4y−16=0
View SolutionIn the previous problem, the maximum range of movement of the centre of the part of the circle from line AD in which charged particle of charge Q moves with a velocity v when (θ) is positive to when (θ) is negative is given by
View SolutionIn the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and CD respectively. If OL=OM and AB=16cm, then find the length of CD.
 View Solution
View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionIf the perpendicular distance of the line lx+my=1 from the point (0, 0) is a, then the diameter of the circle touching the given line and with centre (0, 0) is
View SolutionIn the given figure, O is the centre of the circle and OLM is perpendicular to AOB. Prove that (i) A, O, P and M are concyclic (ii) ∠OAP=∠OMB (iii) P, L, O and B are concyclic
View Solution

