Let I1andI2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron.
I1<I2
I1=I2
I1>I2
Relation between I1 and I2 depends on the actual shapes of the bodies
The correct Answer is:A
To solve the problem, we need to analyze the moments of inertia of two bodies made of different materials but having identical geometrical shapes. Let's break down the solution step by step.
1. Understand the Moment of Inertia Formula:
The moment of inertia I of a body can be expressed as:
I=m⋅k2
where m is the mass of the body and k is the radius of gyration.
2. Relate Mass to Density and Volume:
The mass m of an object can be expressed in terms of its density ρ and volume V:
m=ρ⋅V
Therefore, we can rewrite the moment of inertia as:
I=ρ⋅V⋅k2
3. Identify Common Parameters:
Since both bodies have identical geometrical shapes, they will have the same volume V and the same radius of gyration k. Thus, we can denote:
I1=ρAl⋅V⋅k2
for aluminum and
I2=ρFe⋅V⋅k2
for iron.
4. Compare Densities:
It is known that the density of iron ρFe is greater than the density of aluminum ρAl:
ρFe>ρAl
5. Establish the Relationship Between Moments of Inertia:
Since both bodies have the same volume and radius of gyration, we can conclude:
I2=ρFe⋅V⋅k2>ρAl⋅V⋅k2=I1
Therefore, we have:
I2>I1
6. Final Conclusion:
From the above analysis, we conclude that the moment of inertia of the iron body I2 is greater than that of the aluminum body I1. Thus, the correct answer is:
I2>I1
The moment of inertia I of a body can be expressed as:
I=m⋅k2
where m is the mass of the body and k is the radius of gyration.
The mass m of an object can be expressed in terms of its density ρ and volume V:
m=ρ⋅V
Therefore, we can rewrite the moment of inertia as:
I=ρ⋅V⋅k2
Since both bodies have identical geometrical shapes, they will have the same volume V and the same radius of gyration k. Thus, we can denote:
I1=ρAl⋅V⋅k2
for aluminum and
I2=ρFe⋅V⋅k2
for iron.
It is known that the density of iron ρFe is greater than the density of aluminum ρAl:
ρFe>ρAl
Since both bodies have the same volume and radius of gyration, we can conclude:
I2=ρFe⋅V⋅k2>ρAl⋅V⋅k2=I1
Therefore, we have:
I2>I1
From the above analysis, we conclude that the moment of inertia of the iron body I2 is greater than that of the aluminum body I1. Thus, the correct answer is:
I2>I1
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples29videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
Statement - 1 : Let I1andI2 be the moment of inertia of two bodies of identical geometrical shapes, the first made of aluminium and second of iron then I1<I2. Becaause
Statement - 2 : Moment of inertia does not depends on shapeView SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View Solution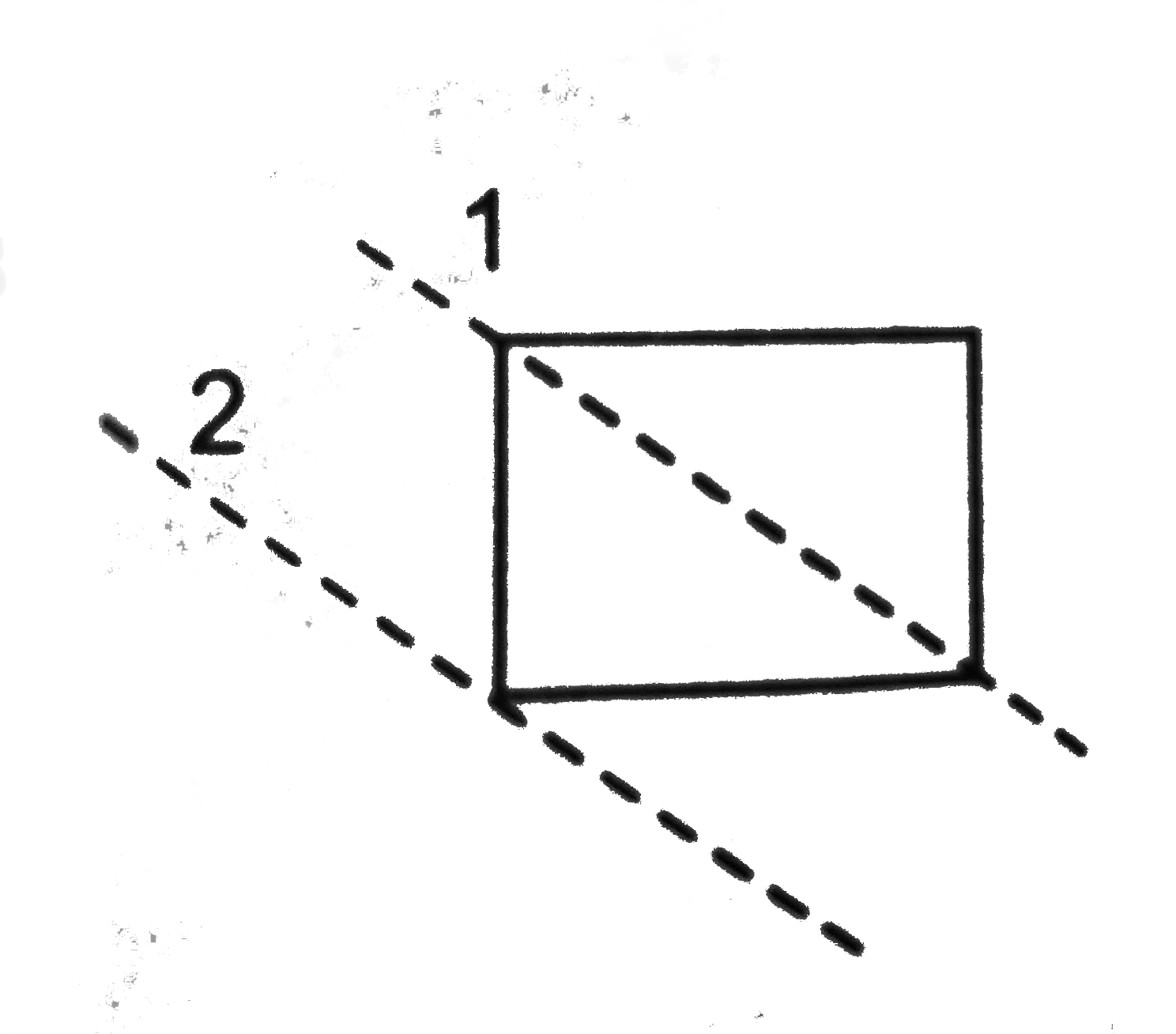
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 isView SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionLet IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionA rigid body is rotating about a vertical axis. In t second, the axis gradually becomes horizontal. But the rigid body continues to make v rotations per second throughout the time interval of 1 second. If the moment of inertia I of the body about the axis of rotation can he taken as constant, then the torque acting on the body is
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
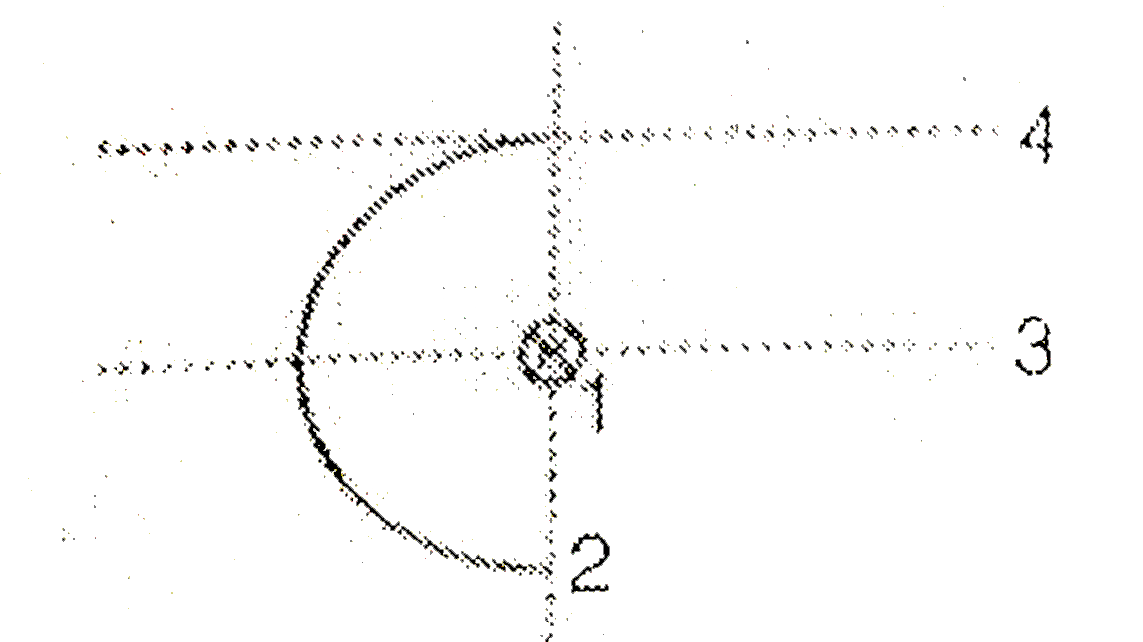
 View Solution
View SolutionIf I1,I2 and I3 are the moments of inertia about the natural axies of solid sphere, hollow sphere and a spherical shell of same mass and radii, the correct result of the following is
View Solution

