One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
2π√mk
2π√m(YA+kL)YAK
2π√m(YA+kL)AK
2π√m(Y+kL)YAK
The correct Answer is:B
To solve the problem, we need to find the time period T of the oscillation of a mass m attached to a spring and a wire. We will consider the spring constant of the wire and the spring in series to find the equivalent spring constant.
1. Identify the Components:
- We have a mass m hanging from a spring with spring constant K.
- The mass is also attached to a wire of length L, cross-sectional area A, and Young's modulus Y.
2. Calculate the Spring Constant of the Wire:
- The spring constant K1 of the wire can be derived from the formula for Young's modulus:
Y=StressStrain=F/AΔL/L
- Rearranging gives:
F=Y⋅A⋅ΔLL
- The spring constant K1 is defined as the force per unit extension:
K1=FΔL=Y⋅AL
3. Combine the Spring Constants:
- The effective spring constant Keq for two springs in series (the spring and the wire) is given by:
1Keq=1K+1K1
- Substituting K1:
1Keq=1K+LY⋅A
- Taking the reciprocal gives:
Keq=K⋅(Y⋅A)Y⋅A+K⋅L
4. Calculate the Time Period:
- The time period T of the oscillation is given by:
T=2π√mKeq
- Substituting Keq:
T=2π√m⋅(Y⋅A+K⋅L)K⋅(Y⋅A)
Final Expression for Time Period:
The time period T can be expressed as:
T=2π√m⋅(Y⋅A+K⋅L)K⋅(Y⋅A)
- We have a mass m hanging from a spring with spring constant K.
- The mass is also attached to a wire of length L, cross-sectional area A, and Young's modulus Y.
- The spring constant K1 of the wire can be derived from the formula for Young's modulus:
Y=StressStrain=F/AΔL/L
- Rearranging gives:
F=Y⋅A⋅ΔLL
- The spring constant K1 is defined as the force per unit extension:
K1=FΔL=Y⋅AL
- The effective spring constant Keq for two springs in series (the spring and the wire) is given by:
1Keq=1K+1K1
- Substituting K1:
1Keq=1K+LY⋅A
- Taking the reciprocal gives:
Keq=K⋅(Y⋅A)Y⋅A+K⋅L
- The time period T of the oscillation is given by:
T=2π√mKeq
- Substituting Keq:
T=2π√m⋅(Y⋅A+K⋅L)K⋅(Y⋅A)
The time period T can be expressed as:
T=2π√m⋅(Y⋅A+K⋅L)K⋅(Y⋅A)
Similar Questions
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
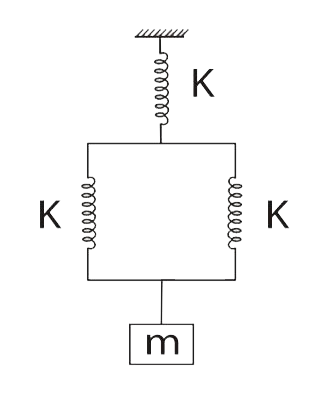
View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
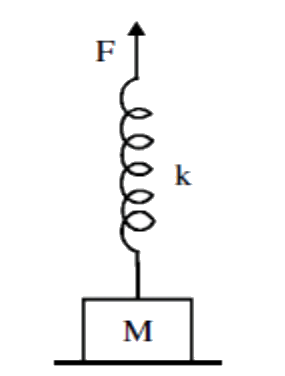
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
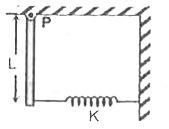
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is +(12)kx2. The possible cases are.
View Solution
