State Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
Consider an infinitely long straight charged wire of linear charge desnsity λ. To find electric field at a point P situated at a distance r from the wire by using Guass. law consider a cylinder of length l and radius r as the Gaussian surface.
From symmetry consideration electric field at each point of its curved surface is →E and is point outwards normally . Therefore, electric flux over the curved surface.
∫→Eˆnds=E2πrl
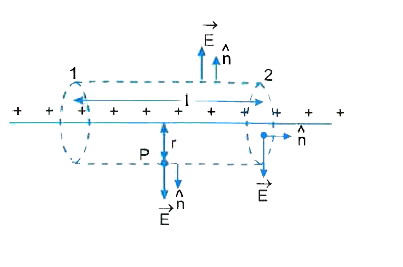
On the side face 1 and 2 of the cylinder normal drawn on the surface is perpendicular to electric field E and hence these surfaces do not contribute towards the total electric flux.
∴ Net electric flux over the entire Gaussian surface ϕE=E.2πrl
By Gauss law electric flux ϕE=1ε0 (charge enclosed)=lamdbalε0
Comparing (i) and (ii) , we have
E.2πrl=λlε0
⇒E=λ2πε0r
As E∝1r , hence E -r shown in fig.

Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -II
9 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SHORT ANSWER QUESTIONS
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
Similar Questions
State Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View Solution
Knowledge Check
The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
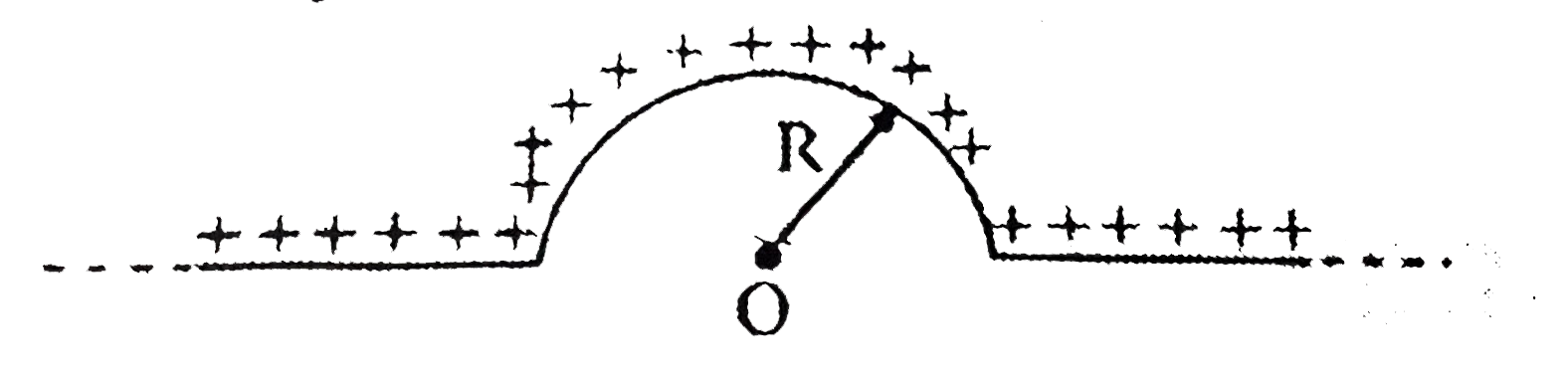 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
State Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
View SolutionAnswer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionState Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density ) at a point lying at a distance r from the wire.
View Solution(a) State Gauss's law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge desntiy λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionAnswer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View Solution
