The string ,the spring and the pulley shown in figure are light. Find the time period of the mass m.
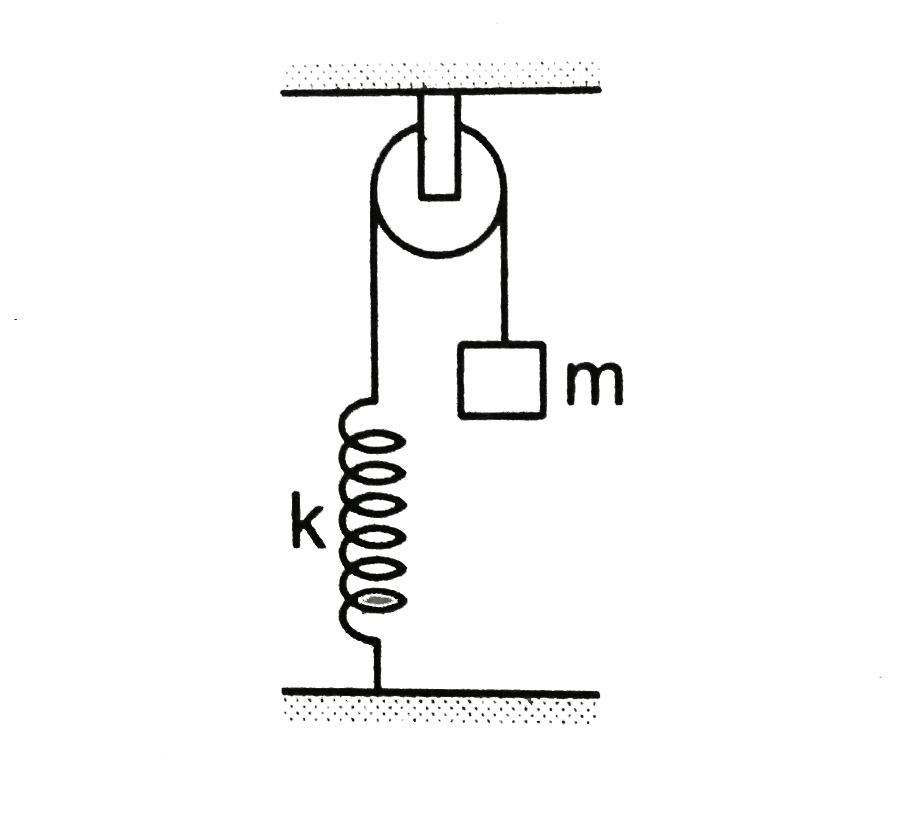
The correct Answer is:2π√mk
When only m is hanging let the extention in the spring be l
So, T1=kl=mg
When a force F is applied let the further extension be x
∴T2−k(x+l)
∴ Driving force =T2−T1=k(x+l)−kl
=Kx
:. Acceleration =Kxm
T=2π√xa
=2π√xkxm=2π√mk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
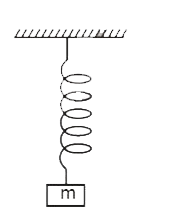
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

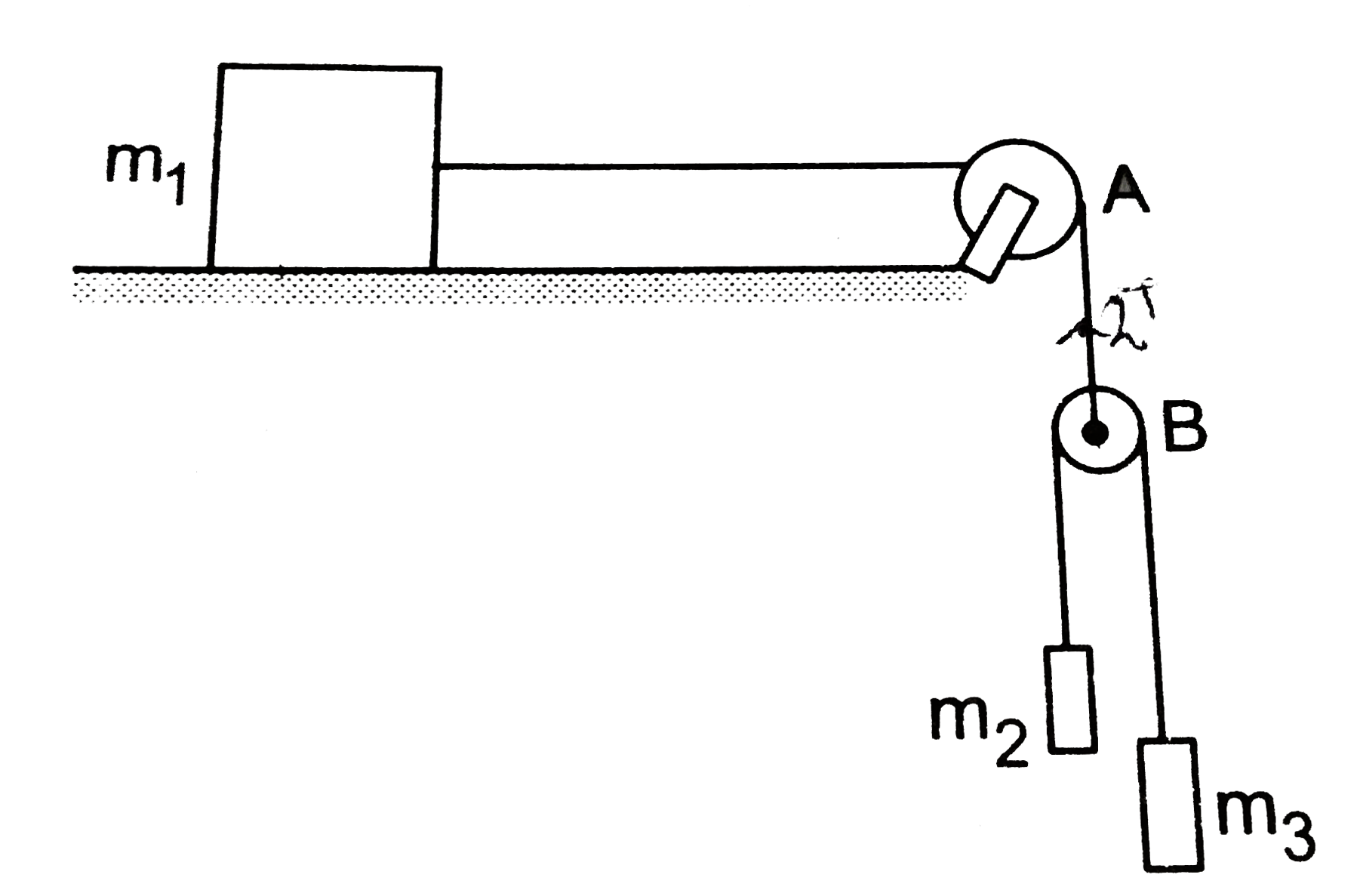
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
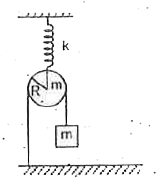
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
View Solution

