Three charges 0.1 coulomb each are placed on the corners of an equilateral triangle of side 1m. If the energy is supplied to this system at the rate of 1kW how much time would be required to move one to the charges on to the midpoint of the line joining the two ?
To solve the problem step by step, we need to calculate the change in potential energy when one charge is moved to the midpoint of the line joining the other two charges, and then determine the time required to supply that energy at a rate of 1 kW.
Step 1: Understand the initial and final configuration
- We have three charges of 0.1 coulomb each placed at the corners of an equilateral triangle with a side length of 1m.
- The initial configuration has charges at points A, B, and C.
- The final configuration has charges at points A, B, and the midpoint M of line AB.
Step 2: Calculate the initial potential energy (U_initial)
The potential energy between two point charges is given by the formula:
\( U = k \frac{q_1 q_2}{r} \)
where \( k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \) (Coulomb's constant), \( q_1 \) and \( q_2 \) are the charges, and \( r \) is the distance between them.
1. Potential energy between charges A and B:
\( U_{AB} = k \frac{q^2}{r} = k \frac{(0.1)^2}{1} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
2. Potential energy between charges A and C:
\( U_{AC} = k \frac{q^2}{r} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
3. Potential energy between charges B and C:
\( U_{BC} = k \frac{q^2}{r} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
4. Total initial potential energy:
\( U_{\text{initial}} = U_{AB} + U_{AC} + U_{BC} = 9 \times 10^7 + 9 \times 10^7 + 9 \times 10^7 = 27 \times 10^7 \, \text{J} \)
Step 3: Calculate the final potential energy (U_final)
In the final configuration, one charge is at the midpoint M between A and B.
1. Potential energy between charges A and B (remains the same):
\( U_{AB} = 9 \times 10^7 \, \text{J} \)
2. Potential energy between charges A and M (distance is \( \frac{1}{2} \)):
\( U_{AM} = k \frac{q^2}{\frac{1}{2}} = 9 \times 10^9 \times 0.01 \times 2 = 18 \times 10^7 \, \text{J} \)
3. Potential energy between charges B and M (distance is \( \frac{1}{2} \)):
\( U_{BM} = k \frac{q^2}{\frac{1}{2}} = 18 \times 10^7 \, \text{J} \)
4. Total final potential energy:
\( U_{\text{final}} = U_{AB} + U_{AM} + U_{BM} = 9 \times 10^7 + 18 \times 10^7 + 18 \times 10^7 = 45 \times 10^7 \, \text{J} \)
Step 4: Calculate the change in potential energy (ΔU)
\( \Delta U = U_{\text{final}} - U_{\text{initial}} = 45 \times 10^7 - 27 \times 10^7 = 18 \times 10^7 \, \text{J} \)
Step 5: Relate energy supplied to time
The energy supplied at a rate of 1kW is:
\( P = 1000 \, \text{W} = 1000 \, \text{J/s} \)
Thus, the energy supplied in time \( t \) is:
\( E = P \times t = 1000 \times t \)
Setting this equal to the change in potential energy:
\( 1000 \times t = 18 \times 10^7 \)
\( t = \frac{18 \times 10^7}{1000} = 1.8 \times 10^5 \, \text{s} \)
Final Answer
The time required to move one of the charges to the midpoint is:
\( t = 1.8 \times 10^5 \, \text{s} \)
---
- We have three charges of 0.1 coulomb each placed at the corners of an equilateral triangle with a side length of 1m.
- The initial configuration has charges at points A, B, and C.
- The final configuration has charges at points A, B, and the midpoint M of line AB.
The potential energy between two point charges is given by the formula:
\( U = k \frac{q_1 q_2}{r} \)
where \( k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \) (Coulomb's constant), \( q_1 \) and \( q_2 \) are the charges, and \( r \) is the distance between them.
\( U_{AB} = k \frac{q^2}{r} = k \frac{(0.1)^2}{1} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
\( U_{AC} = k \frac{q^2}{r} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
\( U_{BC} = k \frac{q^2}{r} = 9 \times 10^9 \times 0.01 = 9 \times 10^7 \, \text{J} \)
\( U_{\text{initial}} = U_{AB} + U_{AC} + U_{BC} = 9 \times 10^7 + 9 \times 10^7 + 9 \times 10^7 = 27 \times 10^7 \, \text{J} \)
In the final configuration, one charge is at the midpoint M between A and B.
\( U_{AB} = 9 \times 10^7 \, \text{J} \)
\( U_{AM} = k \frac{q^2}{\frac{1}{2}} = 9 \times 10^9 \times 0.01 \times 2 = 18 \times 10^7 \, \text{J} \)
\( U_{BM} = k \frac{q^2}{\frac{1}{2}} = 18 \times 10^7 \, \text{J} \)
\( U_{\text{final}} = U_{AB} + U_{AM} + U_{BM} = 9 \times 10^7 + 18 \times 10^7 + 18 \times 10^7 = 45 \times 10^7 \, \text{J} \)
\( \Delta U = U_{\text{final}} - U_{\text{initial}} = 45 \times 10^7 - 27 \times 10^7 = 18 \times 10^7 \, \text{J} \)
The energy supplied at a rate of 1kW is:
\( P = 1000 \, \text{W} = 1000 \, \text{J/s} \)
Thus, the energy supplied in time \( t \) is:
\( E = P \times t = 1000 \times t \)
\( 1000 \times t = 18 \times 10^7 \)
\( t = \frac{18 \times 10^7}{1000} = 1.8 \times 10^5 \, \text{s} \)
The time required to move one of the charges to the midpoint is:
\( t = 1.8 \times 10^5 \, \text{s} \)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
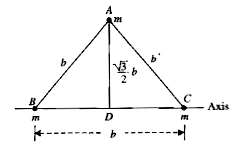 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree equal charges of 5.0μC each are placed at the three vertices of an equilateral triangle of side 5.0cm each. Calculate the electrostatic potential energy of the system of chages.
View Solution
