Two cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

Consider a parallel combination of two cells. Let ε1 and ε2 be the emfs of two cells and r1 and r2 their respective internal resistances. I1 and I2 are the currents leaving the positive electrodes of two cells and at junction B1, these currents are added up so that net current
I=I1+I2 .....(i)
Let V(B1) and V(B2) be the potentials at B1 and B2 , respectively, then considering first cell, we have
V=V(B1)=V(B2)=ε1−I1r1⇒I1=ε1−Vr1 ...(ii)
and considering second cell, we have
V=V(B1)−V(B2)=ε2−I2r2⇒I2=ε2−Vr2
∴I=I1+I2=ε1−Vr1+ε2−Vr2=(ε1r1+ε2r2)−V(1r1−1r2)
⇒V=[(esπ1r1+esπ2r2)−I]/(1r1+1r2)=(ε1r2+ε2r1r1+r2)−I(r1r2r1+r2) ...(iv)
If instead of two cells we join a single cell having equivalent emf εeq and equivalent internal resistance req , then we have
V=εeq−Ireq ....(v)
Thus, comparing (iv) and (v), we get
εeq=(ε1r2+ε2r1r1+r2) and req=r1r2r1+r2
Alternately , we have can write
1req=1r1+1r2 and εeqreq=ε1r1+ε2r2
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS - II
8 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION A (MULTIPLE CHOICE QUESTIONS))
6 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS
42 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
Similar Questions
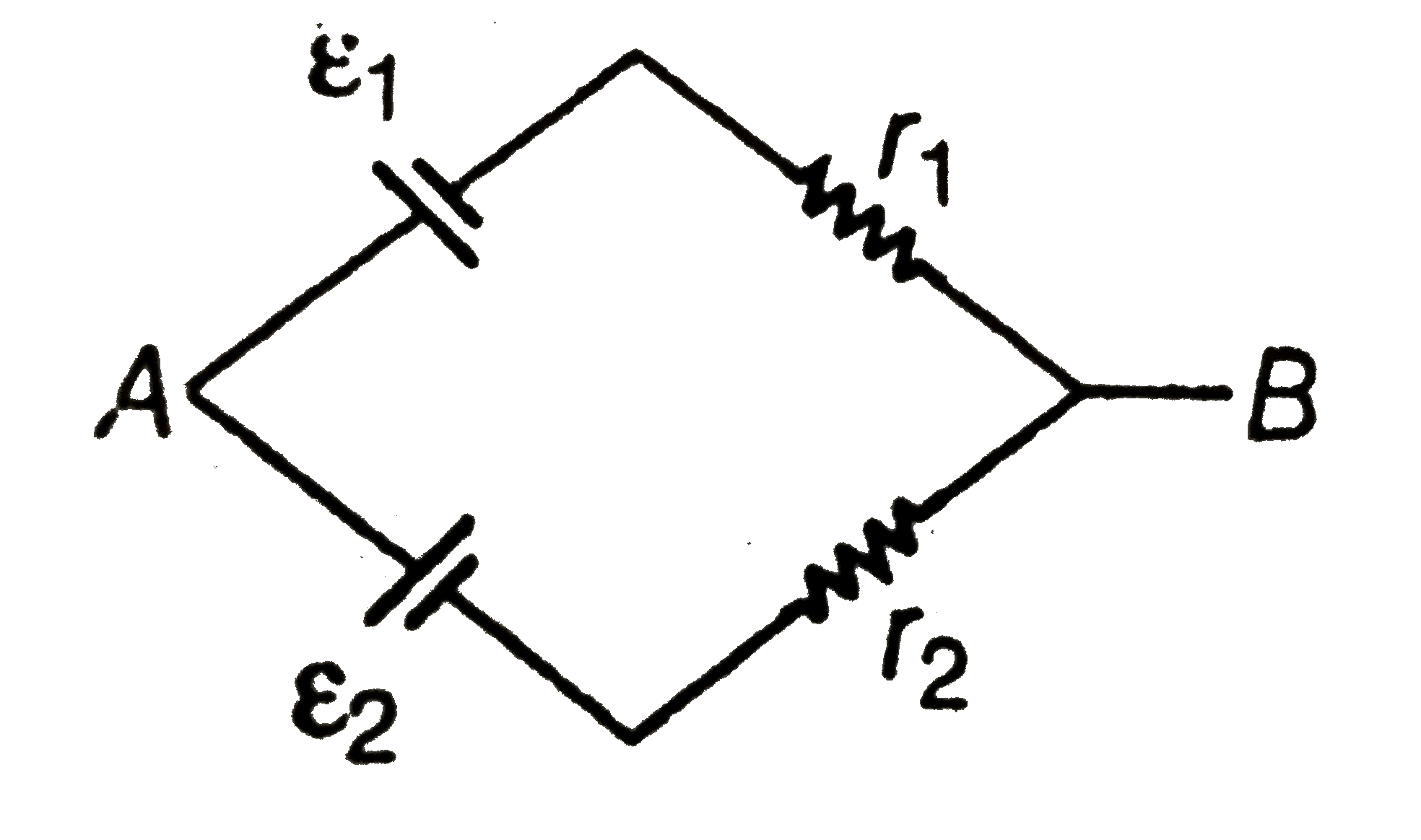
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.
View SolutionTwo cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View Solution
Knowledge Check
Two batteries of emf ε1 and ε2(ε2>ε1) and internal resistances r_1 and r2 respectively are connected in parallel as shown in Fig. Then
 Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.AThe equivalent emf εeq of the two cells is between ε1andε2, i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 always.Dεeq is independent of internal resistance r1andr2.
Two cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionTwo cells of emf E1andE2 having internal resistance r1andr2 are connected in parallel. Calculate Eeq and req for the combination.
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View Solution
