A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
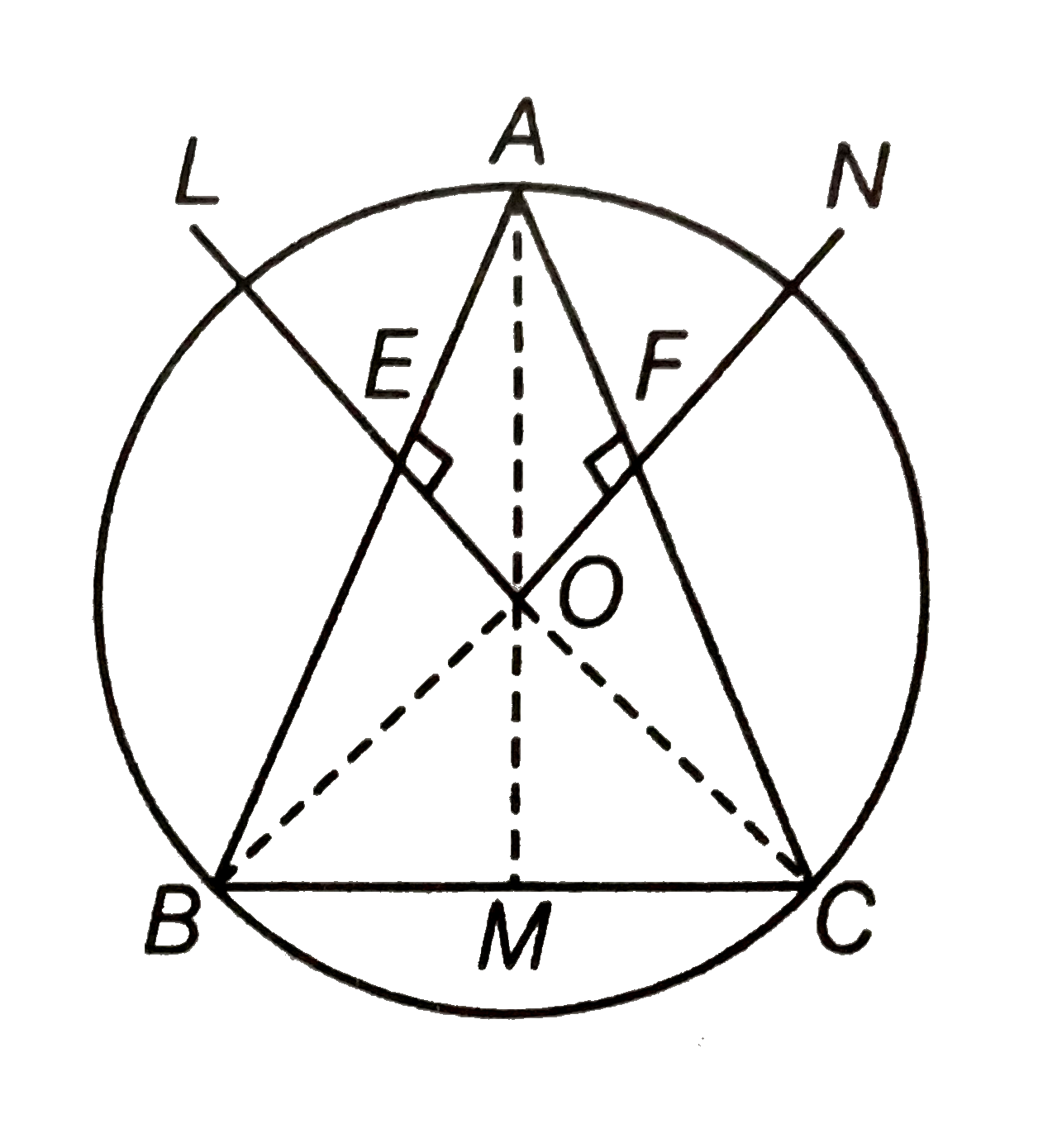
Given A circle passing through three points, A, B and C.
Construction Draw perpendicular bisectors of AB and AC and they meet at a point O. Join OA, OB and OC.
To prove Perpendicular bisector of BC, also passes through O i.e, LO,ON and OM are concurrent.
Proof In ,
AE=BE
[OL is the perpendicular bisector of AB]
and OE=OE [common side]
[by SAS congruence rule]
Similarly, [by SAS congruence rule]
[by CPCT]
[say]
Now, we draw a perpendicular from O to the BC and join them.
In ,
OB=OC [proved above]
OM=OM [common side]
and
[by RHS congruence rule]
[by CPCT]
Hence, OM is the perpendicular bisector of BC.
Hence, OL, ON and OM are concurrent.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
View SolutionProve that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionTwo triangles ABC and PQR are such that the perpendiculars from A to QR ,B to RP and C to PQ are concurrent .Show that the perpendicular from P to BC ,Q to CA and R to AB are also concurrent .
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionFrom an external point two tangents PA and PB are drawn to the circle with center O. Prove that OP is perpendicular bisector of AB.
View SolutionIf A, B and C are three points on a line and B is between A and C then prove that AC - BC = AB.
View SolutionLet ABCandPQR be any two triangles in the same plane. Assume that the perpendiculars from the points A,B,C to the sides QR,RP,PQ respectively are concurrent. Using vector methods or otherwise,prove that the perpendiculars from P,Q,R→BC,CA,AB respectively are also concurrent.
View Solution
