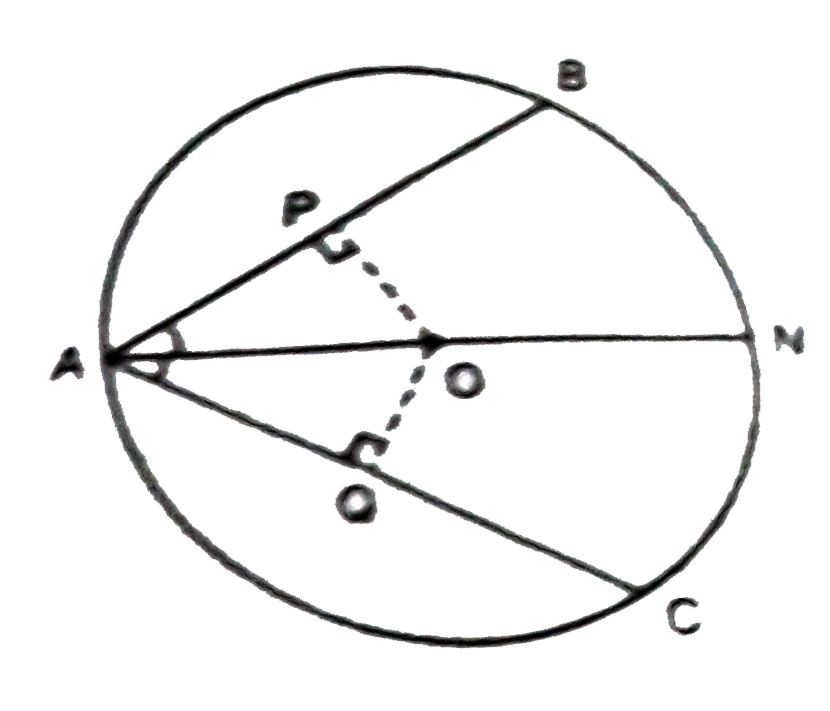
Angle in the same segment of a circle are equal.

Video Solution

Text Solution

Verified by Experts

To prove: $∠ P A Q = ∠ P B Q$
Proof: Chord $P Q$ subtends $∠ P O Q$ at the center.
We know that the angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
$∴ ∠ P A Q = \frac{1}{2} ∠ P O Q$ ...(i)
$∠ P B Q = \frac{1}{2} ∠ P O Q$ .....(ii)
From equation (i) and equation (ii), we get:
$∠ P A Q = ∠ P B Q$
$∴$ Angle in the same segment of a circle are equal.
Hence Proved.

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to :
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Question 2 - Select One
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Question 3 - Select One
Angle formed in minor segment of a circle is
Aacute
Bobtuse
Cright angle
Dnone of these

RD SHARMA-CIRCLE -All Questions

Home
Ask Doubt
Profile