D and E are points on equals sides AB and AC of an isosceles ΔABC such that AD = AE . Prove that the points of B,C,E and D are concyclic.
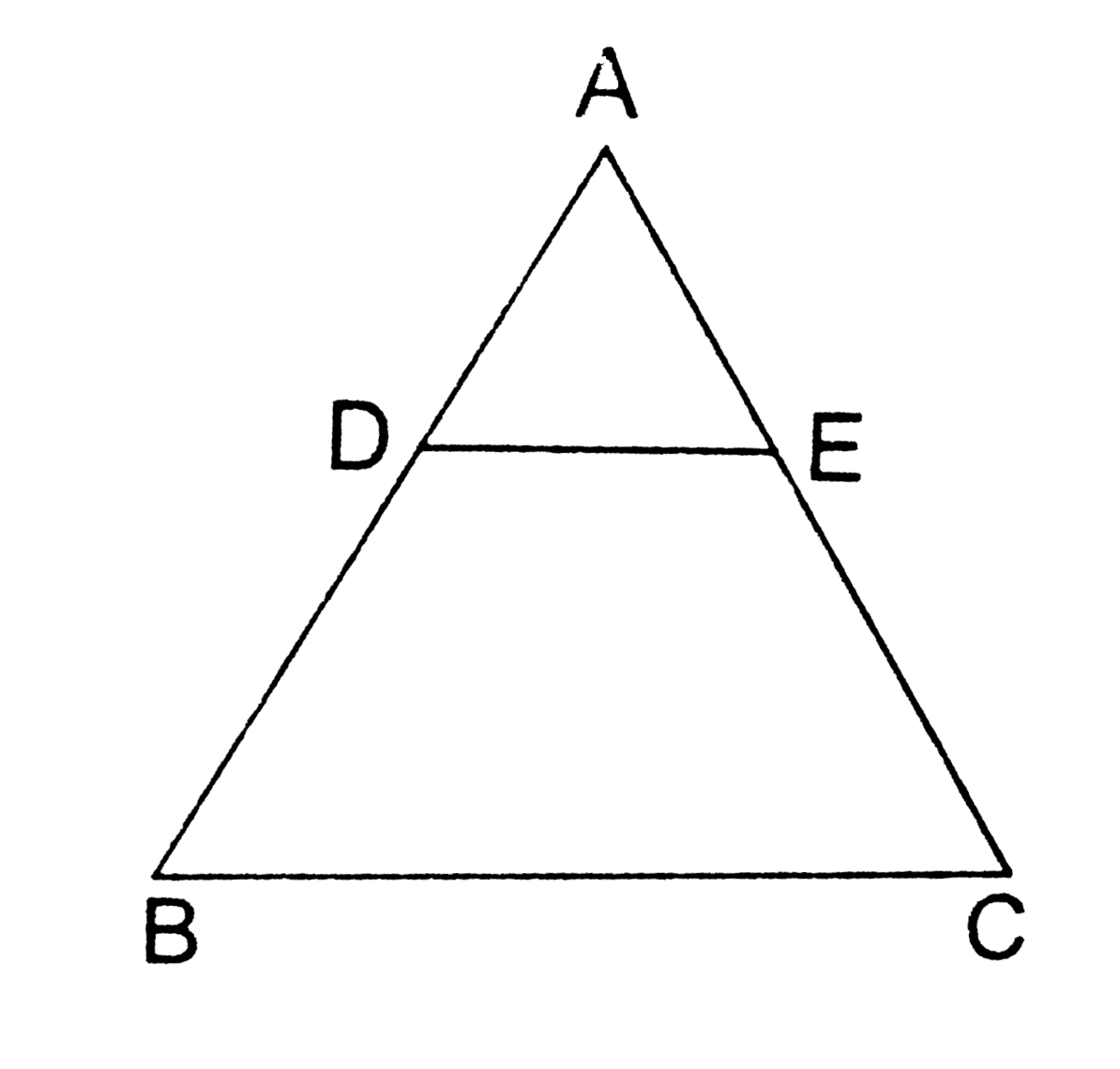
In order to prove that the points B,C,E and D are concyclic, we must show that ∠ECB+∠EDB=180∘
Now, AB=AC⇒∠ABC=∠ACB …..(i)
And, AD=AE⇒∠AED=∠ADE ….(ii)
We know that the sum of the angles of a triangles is 180∘.
∴ in ΔABC and ΔADE, we have
∠A+∠ABC+∠ACB=180∘ and ∠A+∠ADE+∠AED=180∘
⇒∠A+2∠ACB=180∘ and ∠A+2∠ADE=180∘ [using (i) and (ii)]
⇒∠A+2∠ACB=∠A+2∠ADE
⇒2∠ACB=2∠ADE⇒∠ACB=∠ADE .....(iii) [:'∠ACB=∠ECB]
∴∠ECB+∠EDB=∠ADB+∠EDB [ using (iii) ]
=180∘[∵∠ADE+∠EDB= a staright ∠]
Thus, ∠ECB+∠EDB=180∘,
This shows that the points B,C,E and D are concyclic.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
DandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionIf D and E are points on sides AB and AC respectively of a ABC such that DEBC and BD=CE . Prove that ABC is isosceles.
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View Solution
