Doubtnut Promotions Sticky

Draw the graph of the function f(x)=(1+1x)2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

f(x)=(1+1x)x,f(x) is defined if 1+1x>0
⇒x+1x>0⇒(−∞,−1)∪(0,∞)
Now f′(x)=(1+1x)x[ln (1+1x)+x1+1x−1x2]
=(1+1x)(x)[ln (1+11x)−1x+1]
Now (1+1x)x is always positive, hence the sign of the f′(x) depends on the sign of ln (1+1x)−1x+1
Let g(x)=ln (1+1x)−1x+1
g′(x)=11+1x−1x2+1(x+1)2=−1x(x+1)2.
For x∈(0,∞),g′(x)<0.
So g(x) is monotonically decreasing for x∈(0,∞). Thus,
g(x)>limx→∞g(x)
⇒g(x)>0
⇒f′(x)>0
For x∈(−∞,−1),g′(x)>0.
So g(x) is monotonically increasing in its domain.
Also limx→±∞(1+1x)x=e
x→±∞(1+1x)x=e
limx→0+(1+1x)x=1 and limx→1(x+1x)x=∞
From the above discussion the graph of the function is as shown in the following figure.
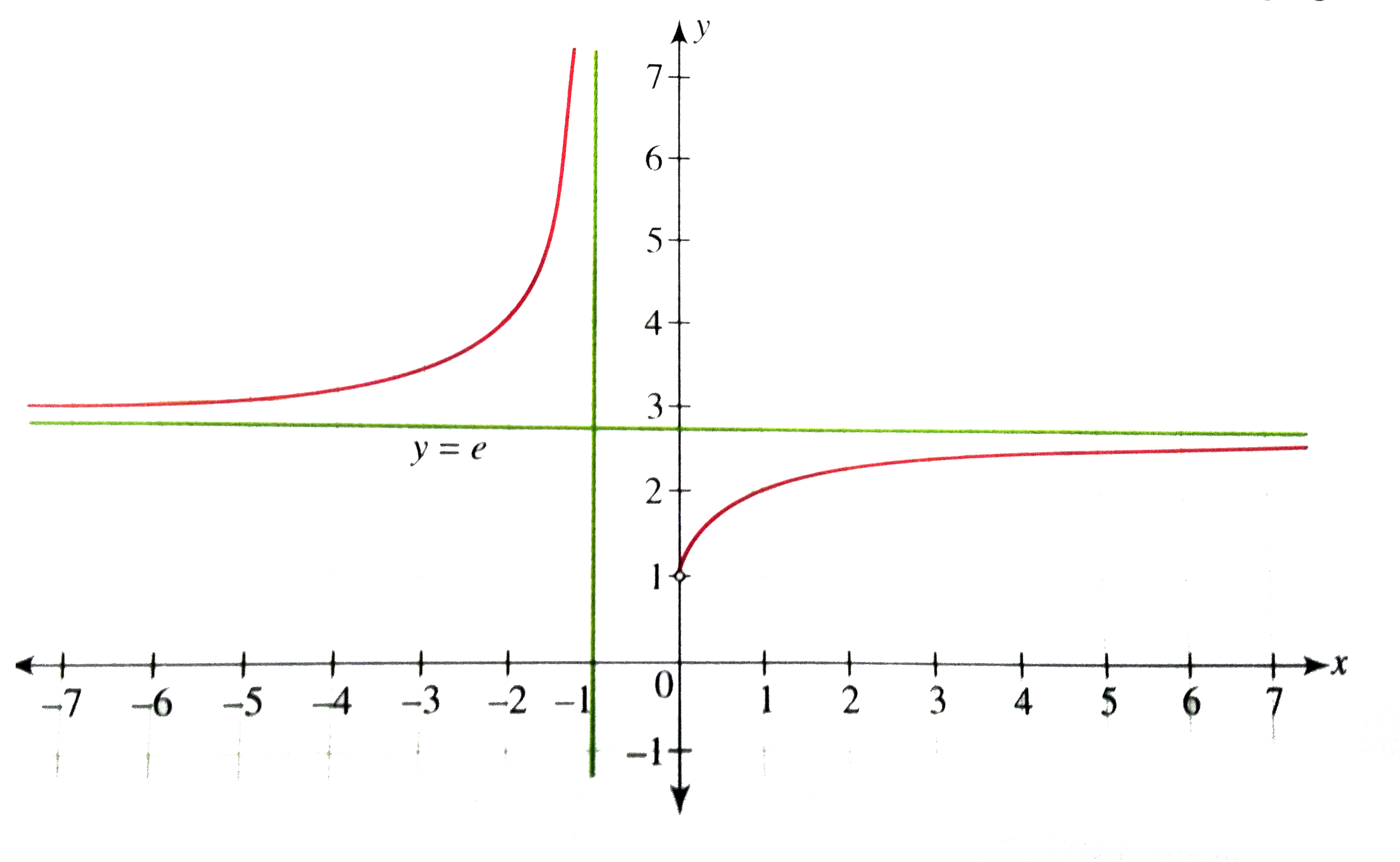
ocr_image
Range is y∈(1,∞)−{e}

|