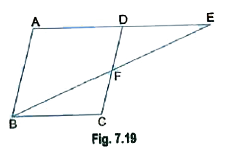
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
To show that triangle ABE is similar to triangle CFB, we will use the Angle-Angle (AA) similarity criterion. Here’s a step-by-step solution:
Step 1: Identify the triangles
We have two triangles to consider: triangle ABE and triangle CFB.
Step 2: Identify the angles in triangle ABE
- Angle BAE (∠BAE) is one angle in triangle ABE.
- Angle AEB (∠AEB) is another angle in triangle ABE.
Step 3: Identify the angles in triangle CFB
- Angle CBF (∠CBF) is one angle in triangle CFB.
- Angle CFB (∠CFB) is another angle in triangle CFB.
Step 4: Show that angle BAE is equal to angle BCF
Since ABCD is a parallelogram, opposite angles are equal. Therefore:
- ∠BAE = ∠BCF (opposite angles of the parallelogram).
Step 5: Show that angle CBF is equal to angle AEB
Since BC is parallel to AD (as opposite sides of a parallelogram), by the Alternate Interior Angle Theorem:
- ∠CBF = ∠AEB.
Step 6: Conclude the similarity of triangles
Now we have:
1. ∠BAE = ∠BCF
2. ∠AEB = ∠CBF
Thus, we can say:
- Triangle ABE ~ Triangle CFB by AA similarity criterion (since two angles of one triangle are equal to two angles of the other triangle).
Final Conclusion
Therefore, triangle ABE is similar to triangle CFB.
---
We have two triangles to consider: triangle ABE and triangle CFB.
- Angle BAE (∠BAE) is one angle in triangle ABE.
- Angle AEB (∠AEB) is another angle in triangle ABE.
- Angle CBF (∠CBF) is one angle in triangle CFB.
- Angle CFB (∠CFB) is another angle in triangle CFB.
Since ABCD is a parallelogram, opposite angles are equal. Therefore:
- ∠BAE = ∠BCF (opposite angles of the parallelogram).
Since BC is parallel to AD (as opposite sides of a parallelogram), by the Alternate Interior Angle Theorem:
- ∠CBF = ∠AEB.
Now we have:
1. ∠BAE = ∠BCF
2. ∠AEB = ∠CBF
- Triangle ABE ~ Triangle CFB by AA similarity criterion (since two angles of one triangle are equal to two angles of the other triangle).
Therefore, triangle ABE is similar to triangle CFB.
Topper's Solved these Questions
Similar Questions
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.Show that ΔABE~ΔCFB.
 View Solution
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE~DCFB .
View SolutionE si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
 View Solution
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
 View Solution
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View Solution

