Find the area bounded by the x-axis, part of the curve $y = (1 - \frac{8}{x^{2}})$ , and the ordinates at $x = 2 a n d x = 4 .$ If the ordinate at $x = a$ divides the area into two equal parts, then find $a .$

A

$\sqrt{2}$ sq units

B

$2 \sqrt{2}$ sq units

C

$3 \sqrt{2}$ sq units

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Area $= \int_{2}^{4} (1 + \frac{8}{x^{2}}) d x$

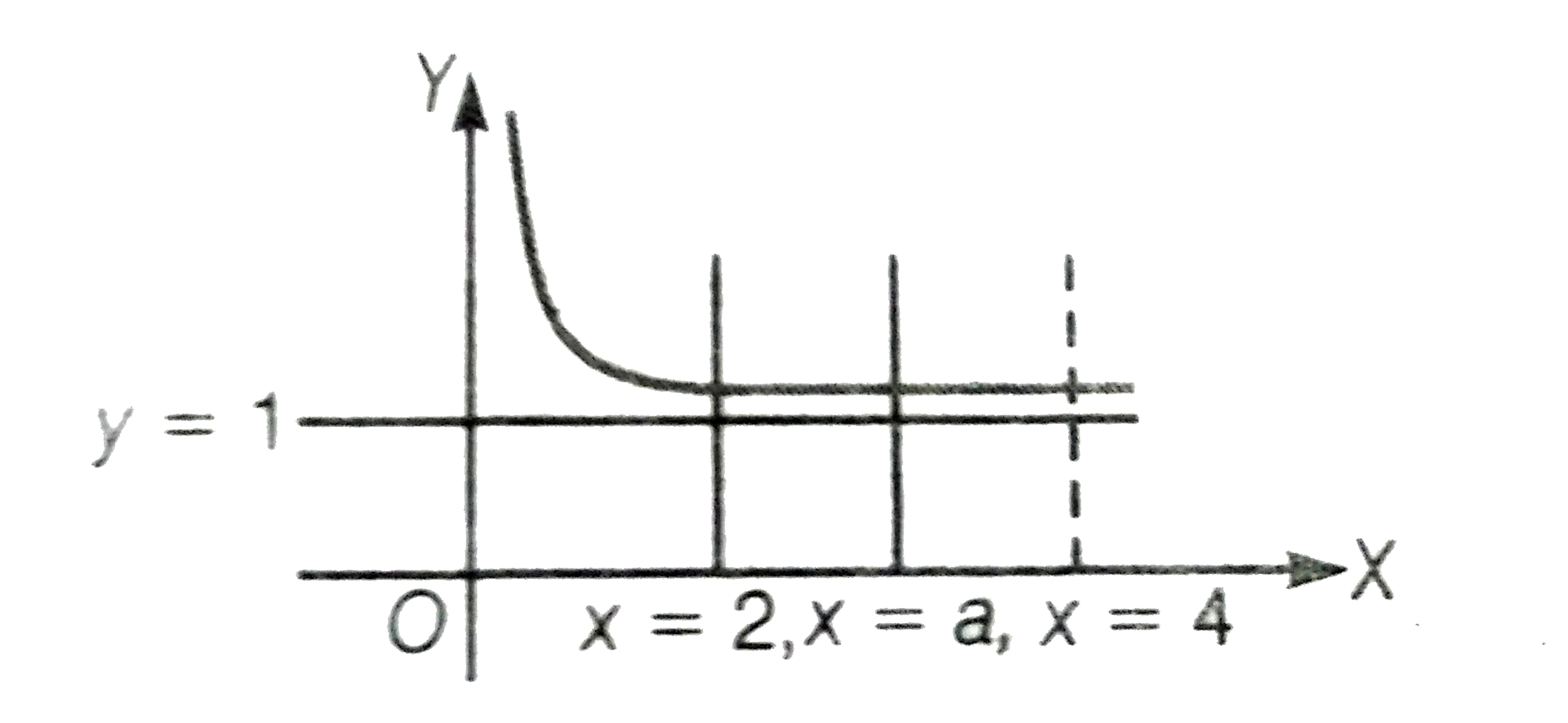
Since, the ordinate x = a divides area into two equal parts, therefore
$\int_{2}^{a} (1 + \frac{8}{x^{2}}) d x = \frac{1}{2} \int_{2}^{4} (1 + \frac{8}{x^{2}}) d x$
$\Rightarrow {[x - \frac{8}{x}]}_{2}^{a} = \frac{1}{2} {[x - \frac{8}{x}]}_{2}^{4}$
$\Rightarrow (a - \frac{8}{a}) - (2 - 4) = \frac{1}{2} [(4 - 2) - (2 - 4)]$
$\Rightarrow a - \frac{8}{a} + 2 = 2 \Rightarrow a = \sqrt{8} = 2 \sqrt{2}$ sq units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let the area bounded by the x- axis, curve $y = (1 + \frac{8}{x^{2}})$ and the ordinates x = 2 and x = 4 is "A" sq. unit and if the ordinate x = a divides the area into two equal parts, then the correct statement among the following is
AA = 3 and a = 2
BA = 2 and a = 1
C $A = 4 \sqrt{2}$ and $a = \sqrt{2}$
DA=4 and $a = 2 \sqrt{2}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -Exercise 2

Home
Ask Doubt
Profile