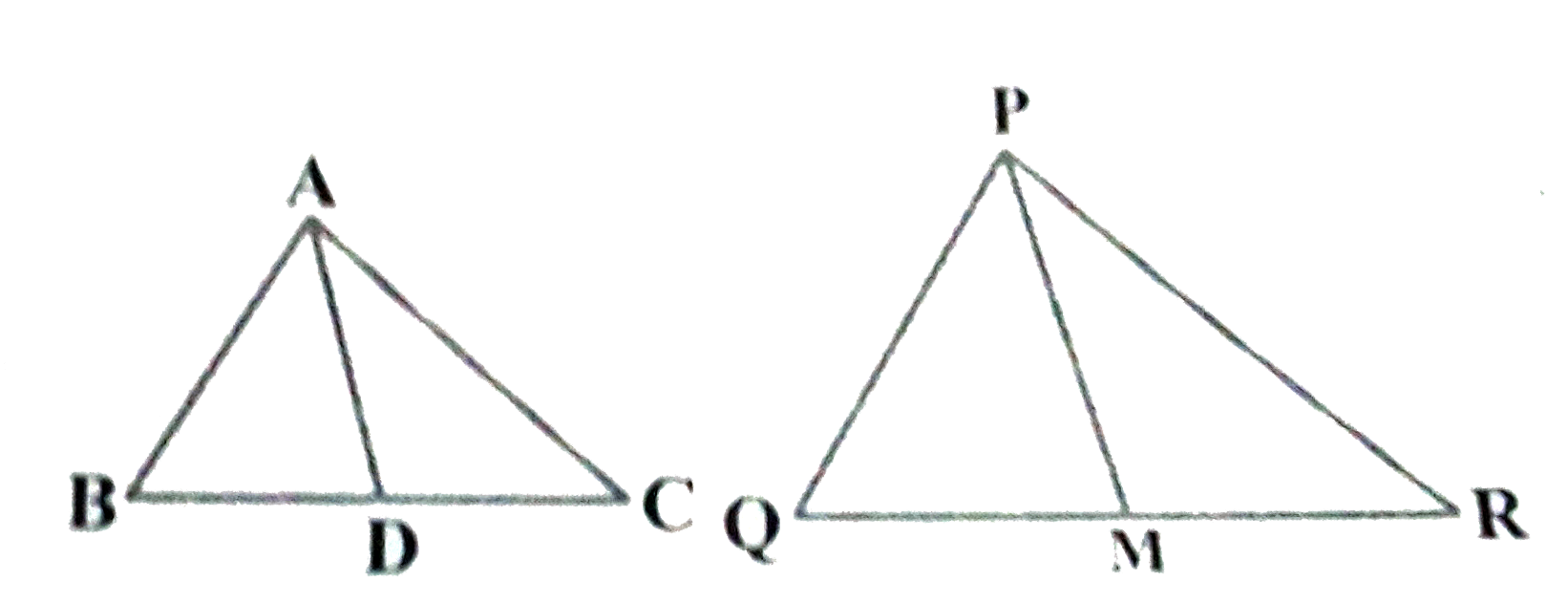
If AD and PM are medians of triangles ABC and PQR, respectively where $Δ A B C ~ Δ P Q R$ , prove that $\frac{A B}{P Q} = \frac{A D}{P M}$

Video Solution

Text Solution

Verified by Experts

from diagram
BD=DC=1/2BC and QM=MR=1/2QR
there ratio should also be same
$\frac{B D}{Q M} = \frac{B C}{Q R} = \frac{A B}{P Q} - (1)$
$∠ A B D ~ ∠ P Q M - (2)$ (SAS)
from 1 and 2
$\frac{A D}{P M} = \frac{A B}{P Q} = \frac{B P}{Q M}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

If AD and PM are medians of triangles ABC and PQR, respectively where $Δ A B C ~ Δ P Q R$ , prove that $\frac{A B}{P Q} = \frac{A D}{P M}$
View Solution
AD and PM are medians of triangles ABC and PQR respectively where $Δ A B C ~ Δ P Q R$ . Prove that: $\frac{A B}{P Q} = \frac{A D}{P M}$ .
View Solution
In figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) $Δ A B C ~ Δ A M P$ (ii) $\frac{C A}{P A} = \frac{B C}{M P}$

View Solution
In figure Cm and RN are respectively the medians of $Δ A B C$ and $Δ P Q R$ . If $Δ A B C ~ Δ P Q R$ , prove that:
(i) $Δ A M C ~ Δ P N R$
(ii) $\frac{C M}{R N} = \frac{A B}{P Q}$
(ii) $Δ C M B ~ Δ R N Q$

View Solution
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of $Δ P Q R$ . Show that $Δ A B C ~ Δ P Q R$ .

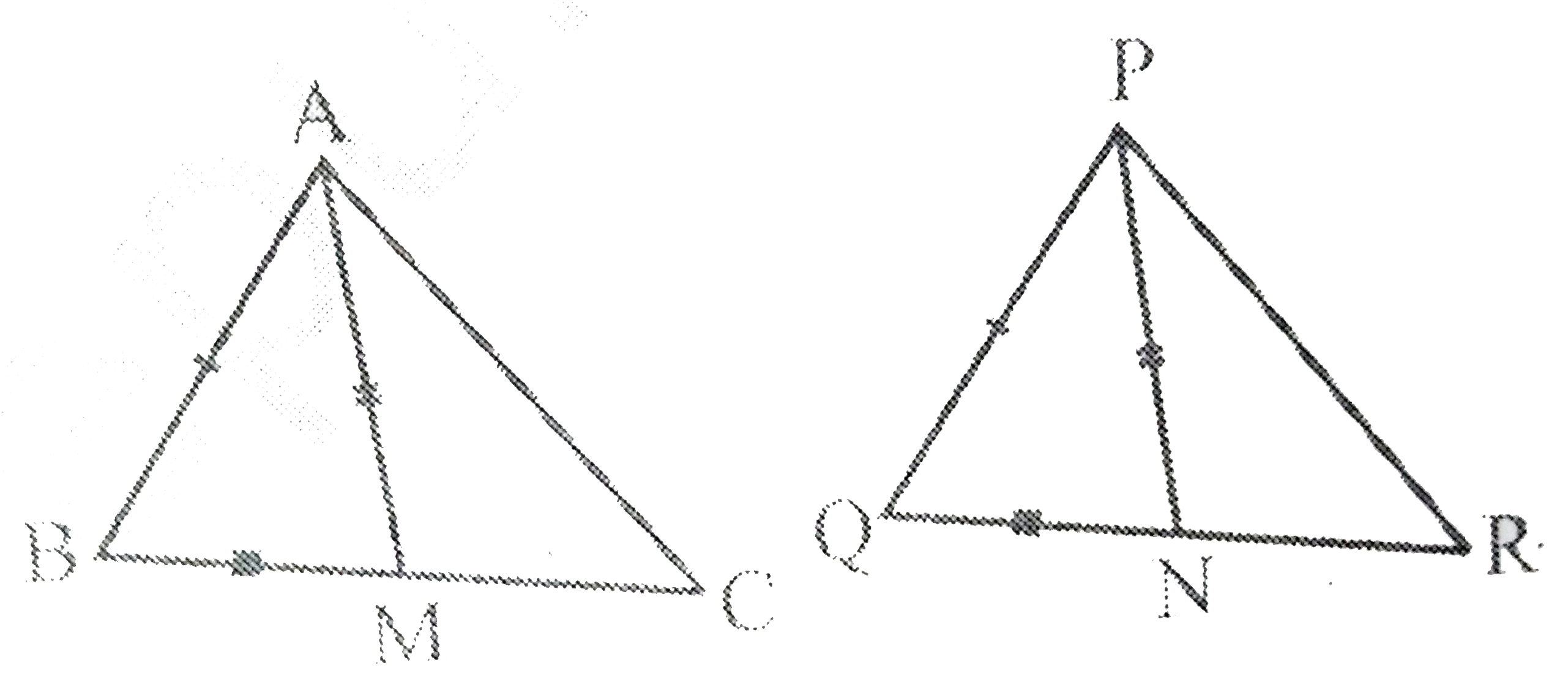
View Solution
Two sides $A B$ and $B C$ and median $A M$ of one triangle ABC are respectively equal to side $P Q$ and $Q R$ and median $P N$ of $Δ A B C ≅ Δ P Q R$ (see Fig. 7.40). Show that:
(i) $Δ A B M ≅ Δ P Q N$
(ii) $Δ A B C ≅ Δ P Q R$

View Solution
In figure PS is the bisector of $∠ Q P R$ of $Δ P Q R$ . Prove that $\frac{Q S}{S R} = \frac{P Q}{P R}$ .

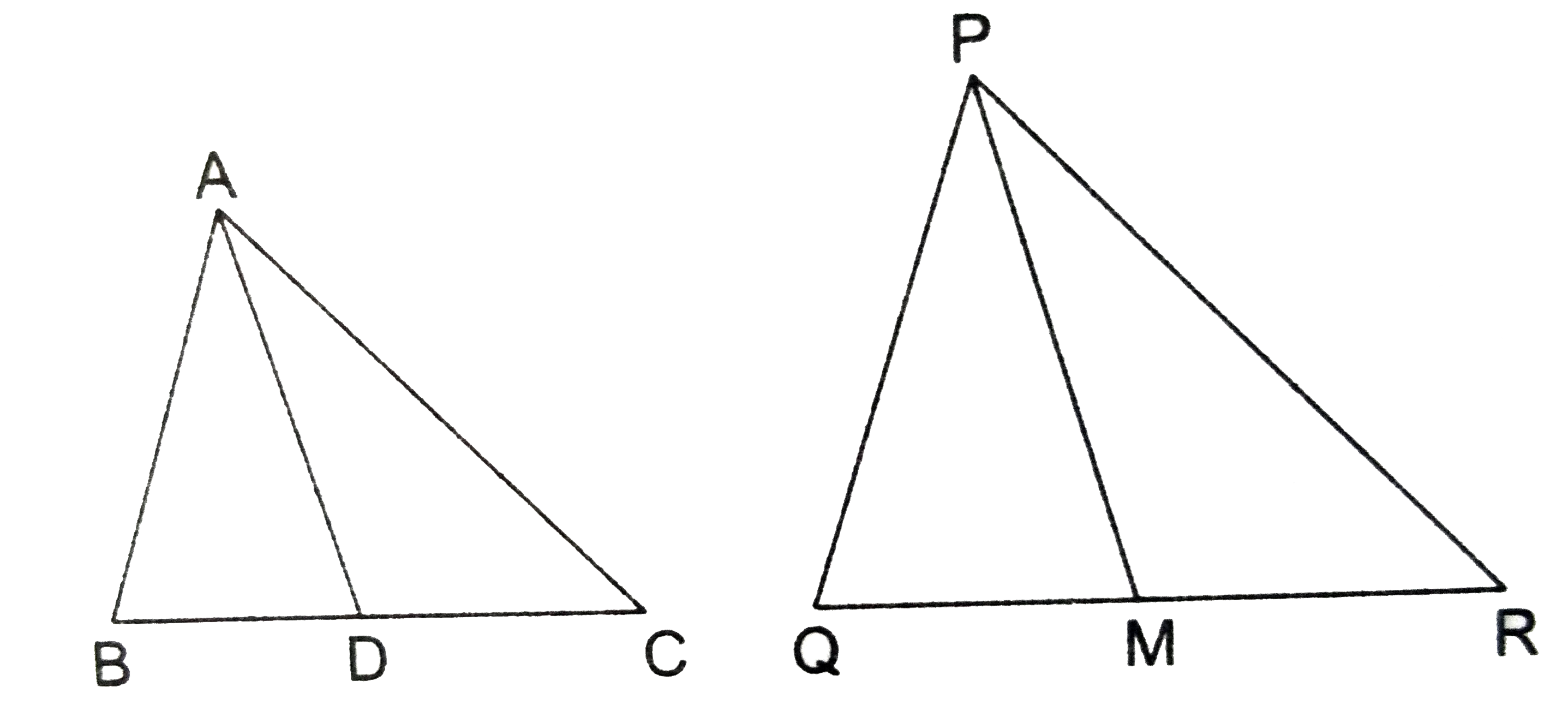
View Solution
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that $Δ A B C ~ D e t l a P Q R$

View Solution
$p A N D q$ are any two points lying on the sides $D C a n d A D$ respectively of a parallelogram $A B C D .$ Show that $a r (A P B) = a r (B Q C) .$
View Solution
Prove that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR $B A C D$ is a parallelogram in which $P, Q, R$ and $S$ are mid-points of the sides $A B, B C, C D$ and $D A$ respectively. $A C$ is a diagonal. Show that : $P Q ∣ ∣ A C$ and $P Q = \frac{1}{2} A C$ $S R ∣ ∣ A C$ and $S R = \frac{1}{2} A C$ $P Q = S R$ (iv) $P Q R S$ is a parallelogram.
View Solution

Recommended Questions

Home
Ask Doubt
Profile