In a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
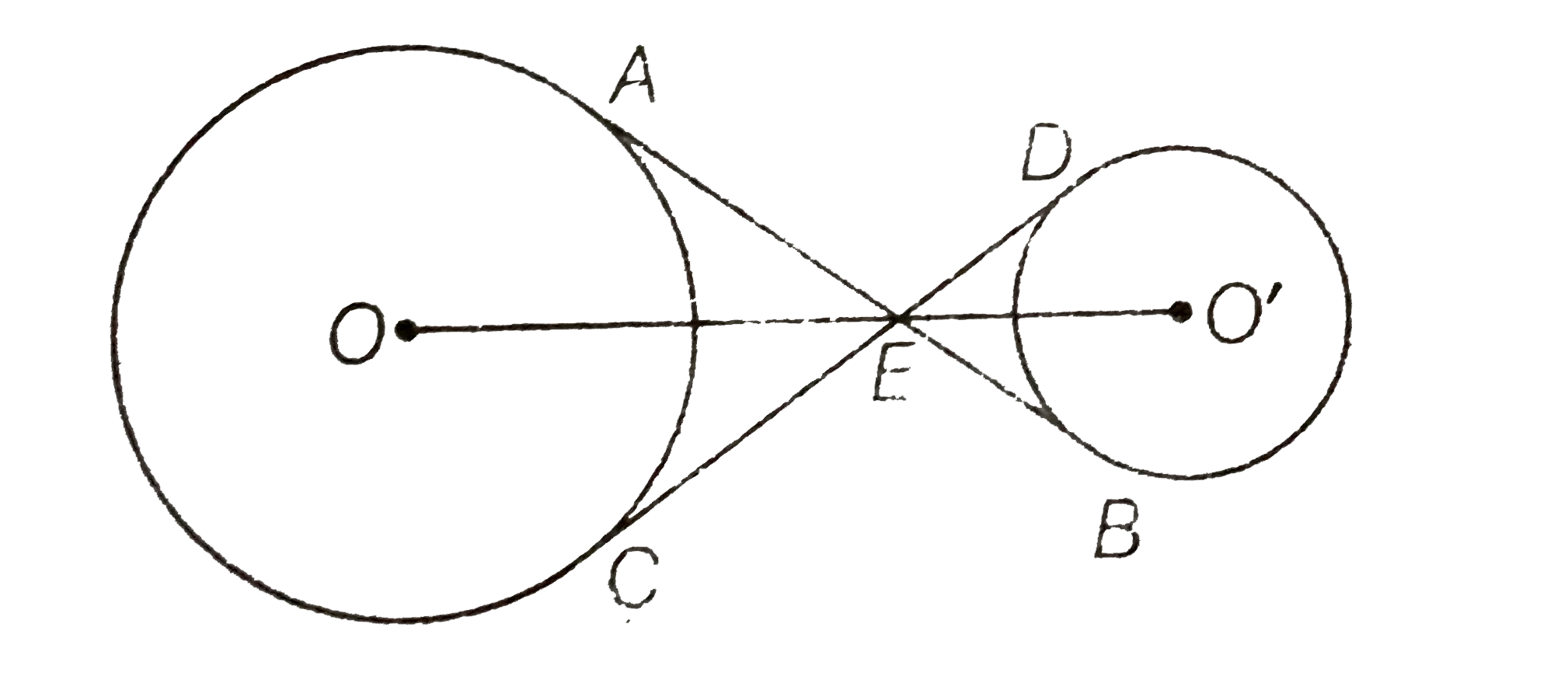
Joint AO, OC and O'D,O'B.
Now, inΔEO'DandΔEO'B,
O'D=O'B [radius] O'E=O'E [common side]
ED=EB
[since, tangents drawn from an external point to the circle are equal in length]
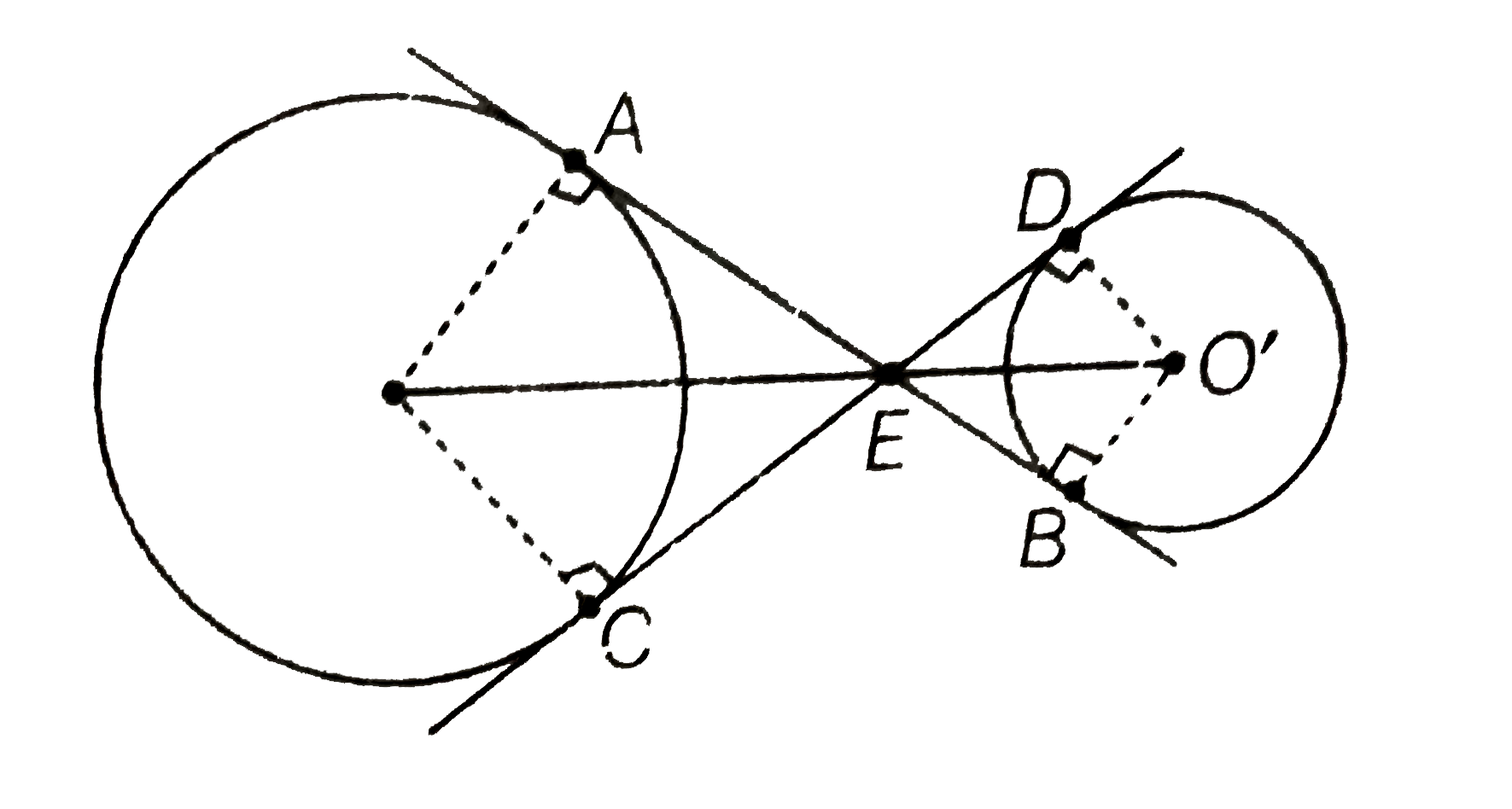
∴ΔEO'D≅ΔEO'B [by SSS congruence rule]
⇒∠O'ED=∠O'EB
O'E is the angle bisector of ∠DEB.....(i)
Similarly, OE is the angle bisector of ∠AEC.
Now, in quadrilateral DEBO'.
∠O'DE=∠O'BE=90∘
[since, CED is a tangent to the circle and O'D is the radius, i.e., O'D⊥CED]
⇒∠O'DE+∠O'BE=180∘
∴∠DEB+∠DO'B=180∘ [since, DEBO' is cyclic quadrilateral]......(ii)
Since, AB is a straight line.
∴∠AED+∠DEB=180∘
⇒∠AED+180∘=∠DO'B=180∘[omEq.(ii)]
⇒∠AED=∠DO'B.....(iii)
Similarly, ∠AED=∠AOC.....(iv)
Again from Eq. (ii), ∠DEB=180∘−∠DO'B
Divided by 2 on both sides, we get
12∠DEB=90∘−12∠DO'B
⇒∠DEO'=90∘−12∠DO'B.....(v)
[since, O'E is the angle bisector of ∠DEB i.e.,12∠DEB=∠DEO]
Similary, ∠AEC=180∘−∠AOC
Divided by 2 on both sides, we get
12∠AEC=90∘−12∠AOC
⇒∠AEO=90∘−12∠AOC......(vi)
[since, OE is the angle bisector of ∠AEC i.e.,12∠AEC=∠AEO]
Now, ∠AED+∠DEO+∠AEO+∠AED+(90∘−12∠DO'B)+(90∘−12∠AOC)
⇒∠AED+180∘−12(∠DO'B+∠AOC)
⇒∠AED+180∘−12(∠AED+∠AED) [from Eqs. (iii) and (iv)]
⇒∠AED+180∘−12(2×∠AED)
⇒∠AED+180∘−∠AED=180∘
∴∠AEO+∠AED+∠DEO'+180∘
So, OEO' is straight line.
Hence, O, E and O' are collinear. Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.
 View Solution
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
 View Solution
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DPView SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.
 View Solution
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD
 View Solution
View Solution

