In Fig. 10.95, PQ and PR are tangents drawn from P to a circle with centre O . If ∠OPQ=35o , then (FIGURE) a=30o, b=60o (b) a=35o, b=55o (c) a=40o, b=50o (d) a=45o, b=45o
To solve the problem, we need to find the angles a and b in the given figure where PQ and PR are tangents to the circle from point P and the angle ∠OPQ=35∘.
1. Identify the Right Triangle:
- In triangle OQP, since PQ is a tangent to the circle at point Q and OQ is the radius, we know that OQ⊥PQ. Therefore, ∠OQP=90∘.
2. Apply the Triangle Sum Property:
- The sum of angles in triangle OQP is 180∘. Thus, we can write:
∠OQP+∠OPQ+∠POQ=180∘
- Substituting the known values:
90∘+35∘+∠POQ=180∘
- Simplifying this gives:
∠POQ=180∘−125∘=55∘
- Therefore, b=55∘.
3. Use Congruent Triangles:
- Since PQ and PR are tangents from point P to the circle, we have PQ=PR. Also, OQ=OR (both are radii of the circle), and OP is common to both triangles OQP and ORP.
- By the Side-Side-Side (SSS) congruence criterion, triangle OQP is congruent to triangle ORP.
4. Determine Angle a:
- Since the triangles are congruent, corresponding angles are equal. Thus:
∠OPQ=∠OPR
- Therefore, a=35∘.
5. Final Values:
- We have found a=35∘ and b=55∘.
Conclusion:
The correct answer is:
a=35∘,b=55∘
This corresponds to option (b).
- In triangle OQP, since PQ is a tangent to the circle at point Q and OQ is the radius, we know that OQ⊥PQ. Therefore, ∠OQP=90∘.
- The sum of angles in triangle OQP is 180∘. Thus, we can write:
∠OQP+∠OPQ+∠POQ=180∘
- Substituting the known values:
90∘+35∘+∠POQ=180∘
- Simplifying this gives:
∠POQ=180∘−125∘=55∘
- Therefore, b=55∘.
- Since PQ and PR are tangents from point P to the circle, we have PQ=PR. Also, OQ=OR (both are radii of the circle), and OP is common to both triangles OQP and ORP.
- By the Side-Side-Side (SSS) congruence criterion, triangle OQP is congruent to triangle ORP.
- Since the triangles are congruent, corresponding angles are equal. Thus:
∠OPQ=∠OPR
- Therefore, a=35∘.
- We have found a=35∘ and b=55∘.
The correct answer is:
a=35∘,b=55∘
This corresponds to option (b).
Topper's Solved these Questions
Similar Questions
In Fig. 10.96, if TP and TQ are tangents drawn from an external points T to a circle with centre O such that ∠TQP=60o , then ∠OPQ= (FIGURE) 25o (b) 30o (c) 40o (d) 60o
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (a) 67o (b) 134o (c) 44o (d) 46o
View SolutionIn Fig. PQ is tangent at a point R of the circle with centre O . If ∠TRQ=30o , find ∠PRS . (FIGURE)
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
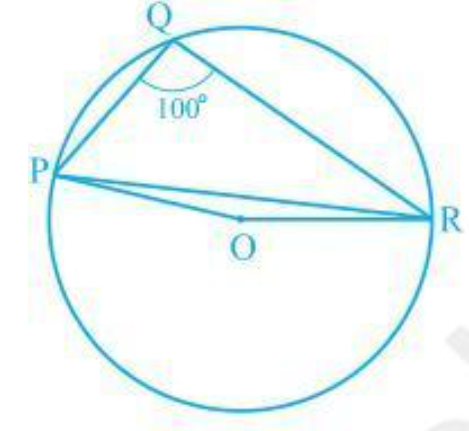
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
 View Solution
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR=120o , then ∠OPQ is 60o (b) 45o (c) 30o (d) 90o
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120∘ . Prove that OP=2 AP .
View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
View Solution

