In Fig. 7.49, ∠B <∠A and ∠C <∠D. Show that AD < BC.
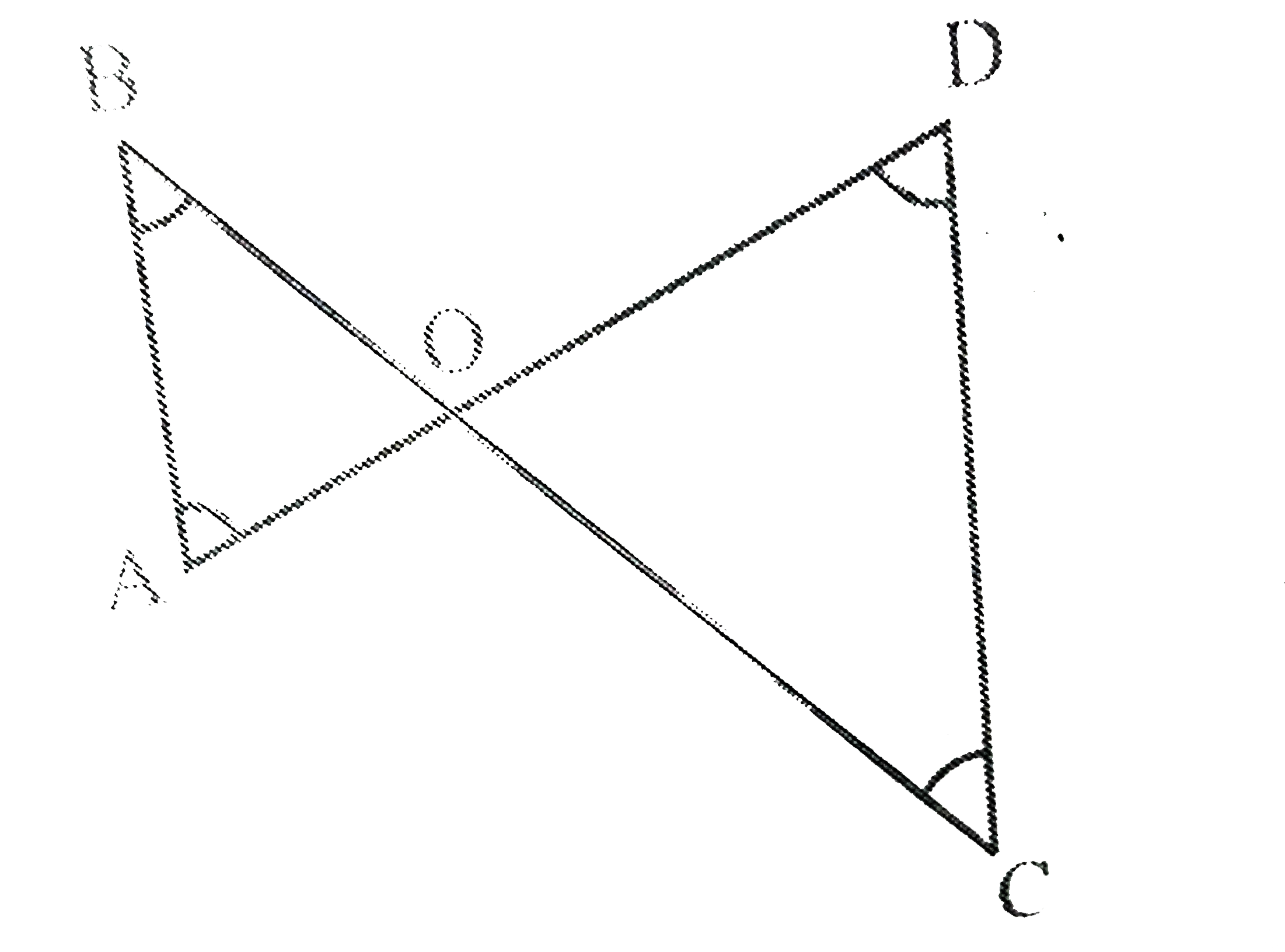

In ΔAOB,∠B<∠A (given)
AO<OB (The side opposite to the smaller angle is smaller) ... (1)
In ΔCOD,∠C<∠D
OD<OC (The side opposite to the smaller angle is smaller) ... (2)
On adding Equations (1) and (2), we obtain
AO+OD<BO+OC
AD<BC
Hence, proved
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Solved Examples9videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.93videos
SURFACE AREAS AND VOLUMES
Similar Questions
Refer to Fig. 7.49.
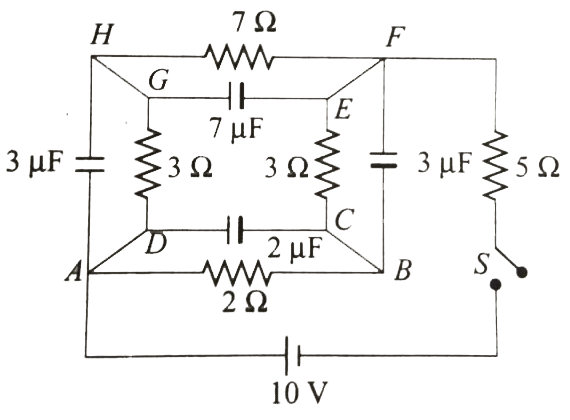
At t=0 , the switch is closed . Just after closing the switch, find the current through the 5Ω resistor.View SolutionIn Fig. 49, m∣∣n and ∠1=650. Find ∠5 and ∠8.
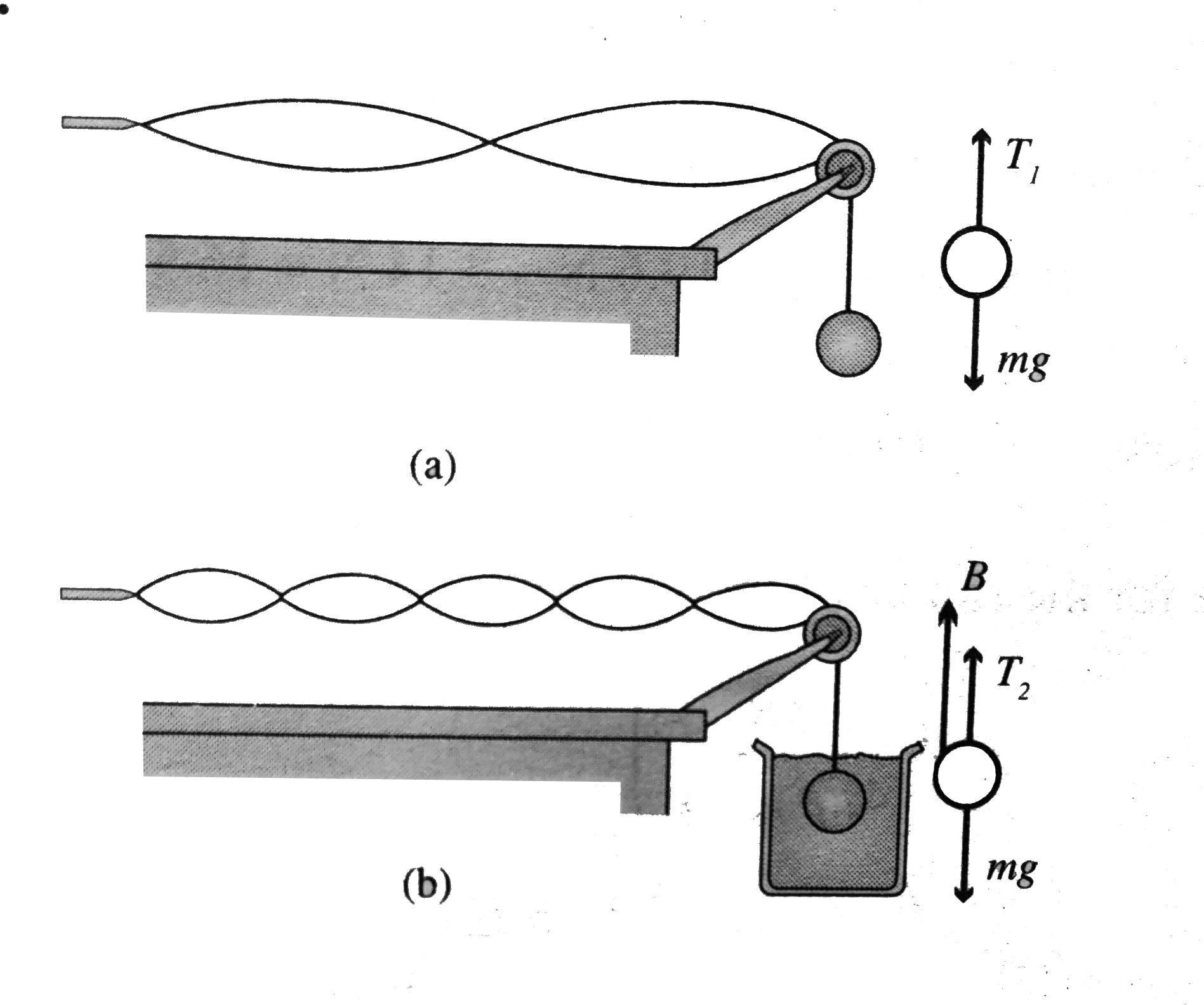
View SolutionOne end of a horizontal string is attached to a vibrating blade , and the other end passes over a pulley as in Fig. 7.49 (a). A sphere of mass 2.00kg hangs at the end of the string . The string is vibrating in its second harmonic . A container of water is raised under the sphere so that the sphere is completely submerged . In this configuration , the string vibrates in its fifth harmonic as shown in Fig . 7.49 (b). What is the radius of the sphere ?
 View Solution
View SolutionIn Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
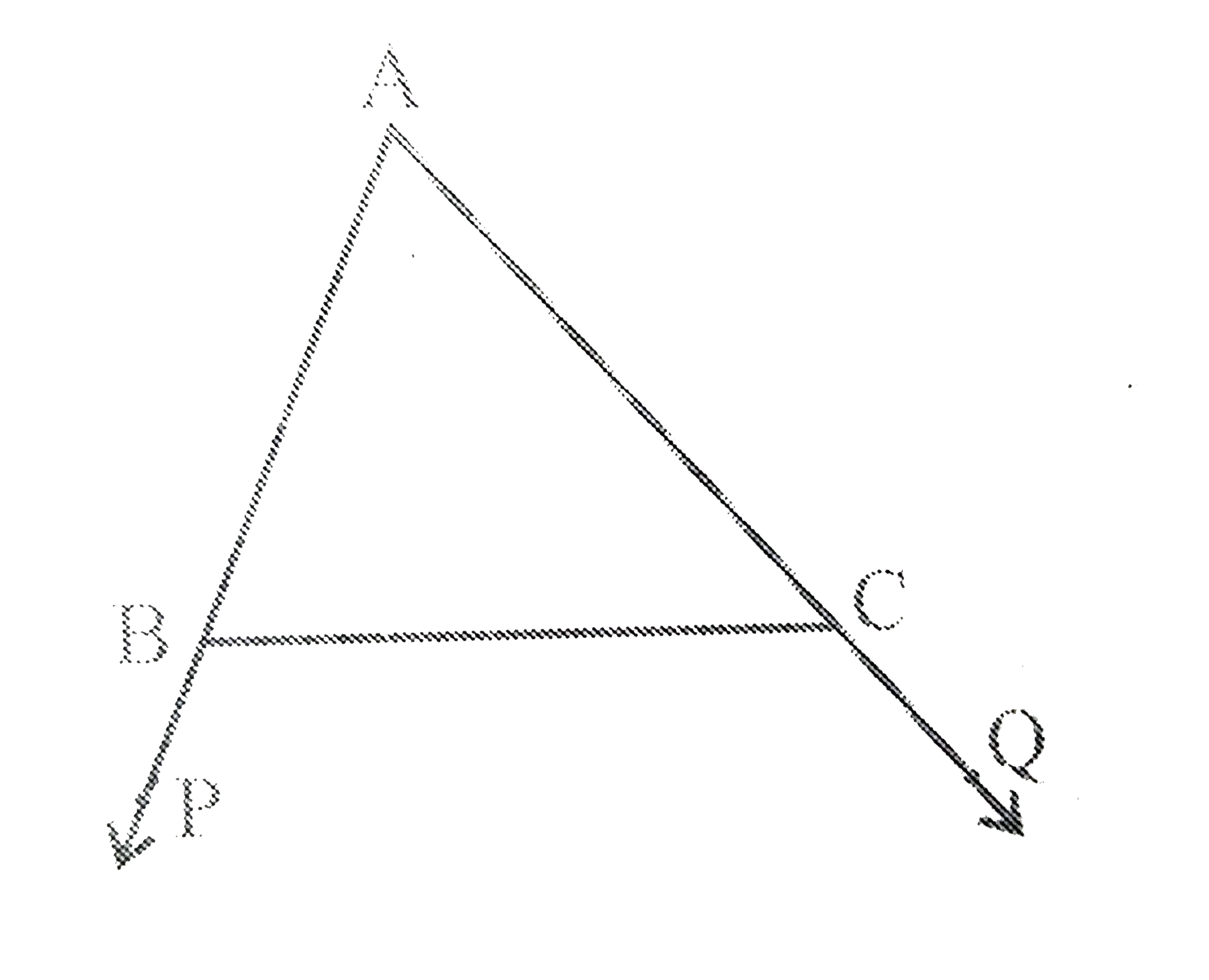 View Solution
View SolutionRefer to Fig. 7.49.
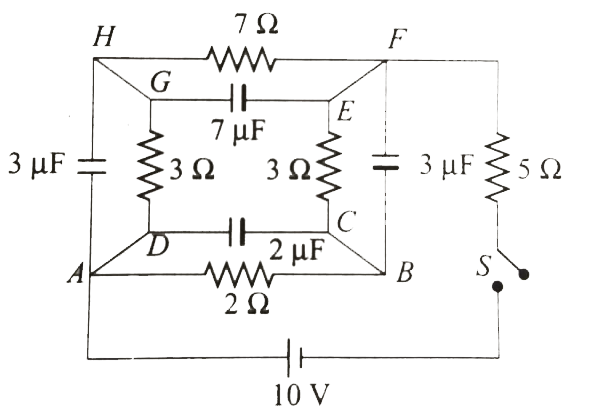
Long time after closing the switch , find the current through the 5Ω resistor.View SolutionIn Fig. , the area of ABC (in square units) is (a) 15 (b) 10 (c) 7.5 (d) 2.5
View Solutionln the network shown in Fig. 5.49. find the equivalent resistance across the points M and M'.
 View Solution
View SolutionIn the circuit in Fig. 7.27, bulb B does not glow although ammeter A indicates that the current is flowing . Why does the bulb not glow?
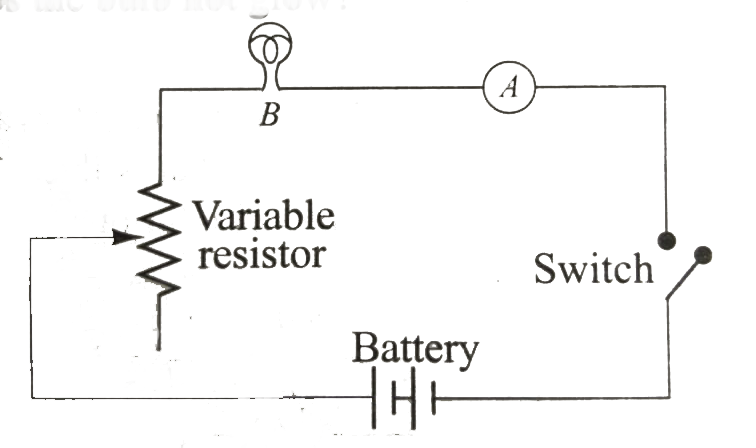 View Solution
View SolutionIn Fig. AB∣∣DC . Find the value of x
View SolutionIn Fig.98, If AB is parallel to CD and EF is a transversal, then x= (a) 19 (b) 29 (c) 39 (d) 49
View Solution

