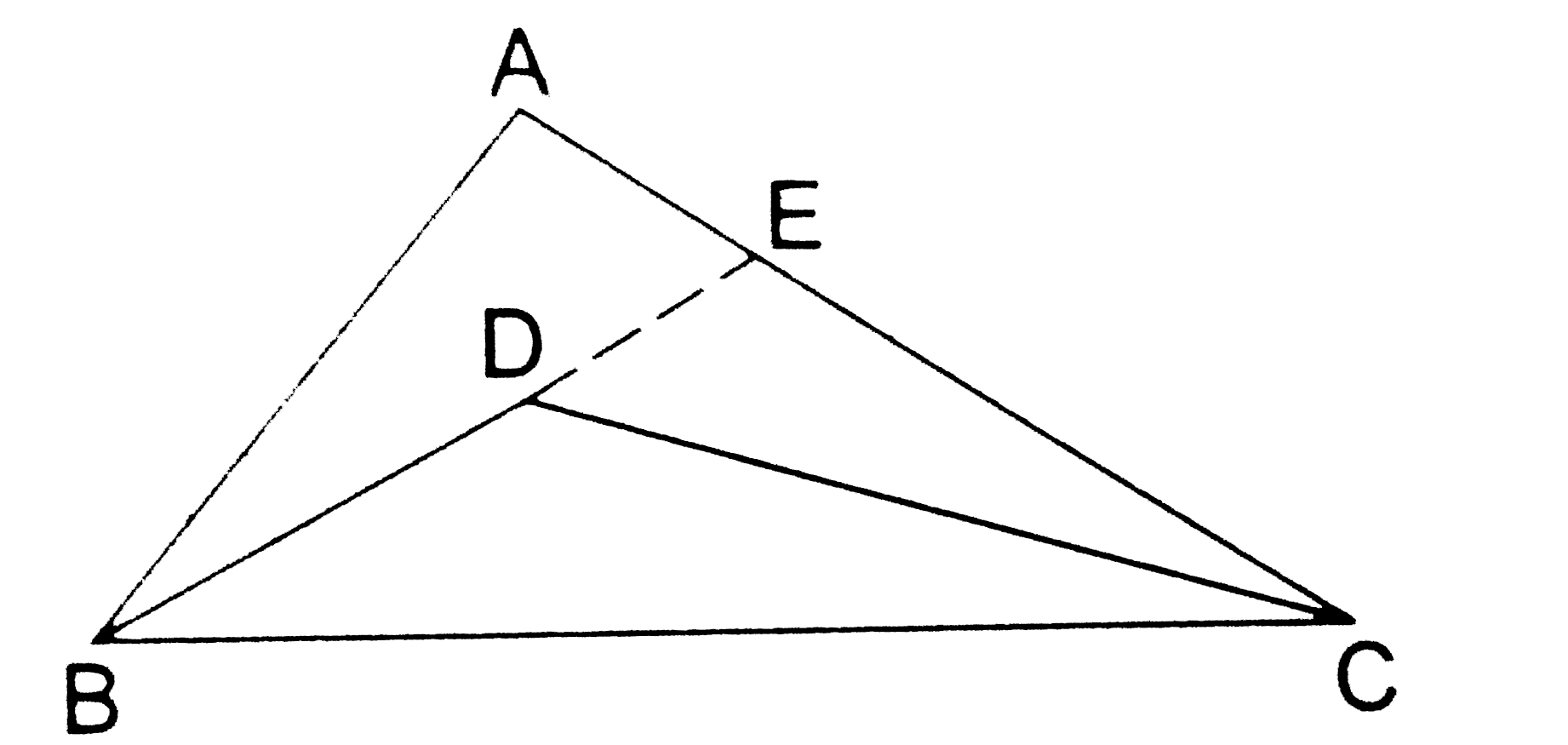
In the adjoining figure, AD and BE are the medians of △ABC and DF||BE. Show that CF=14AC.
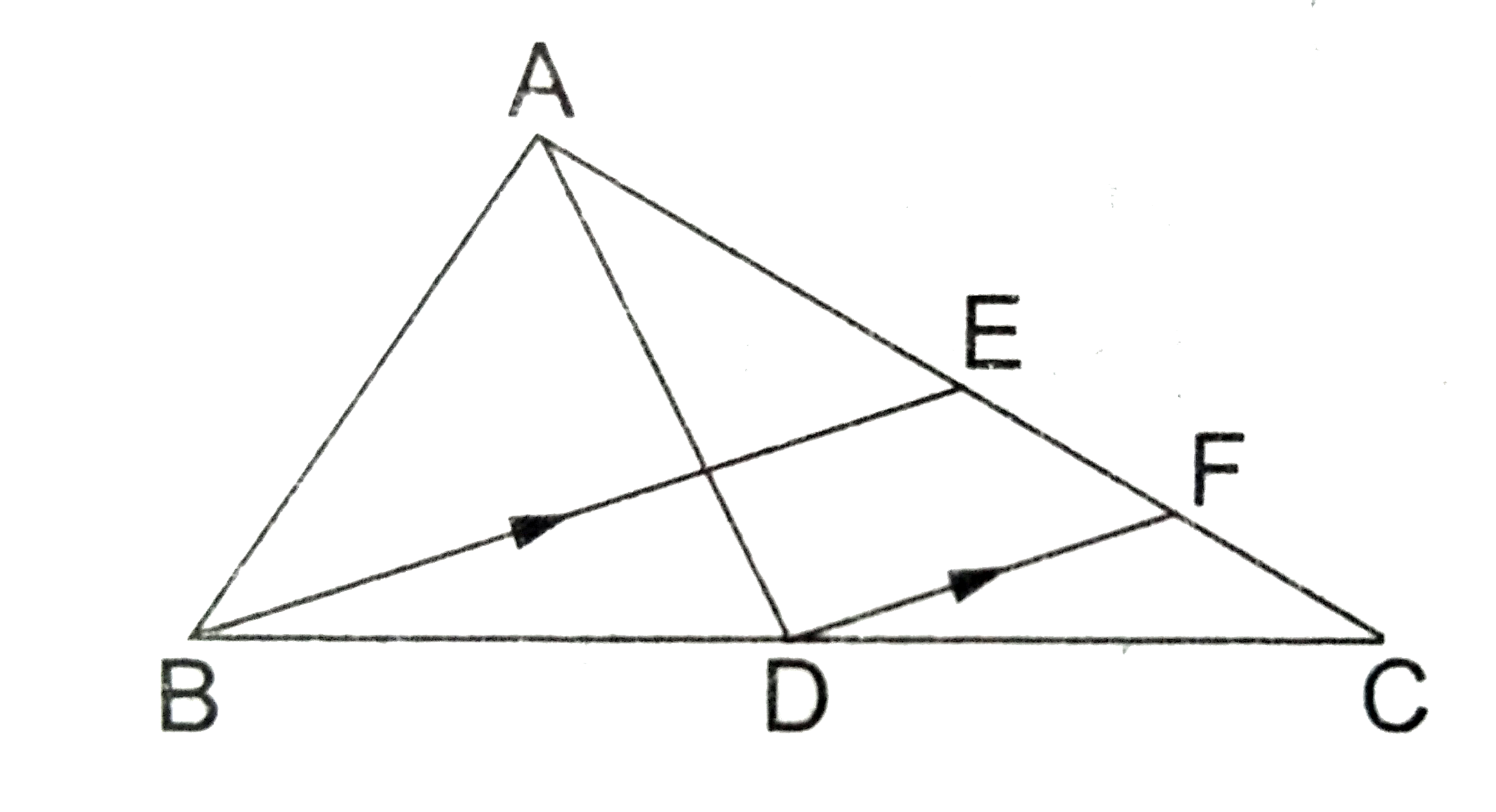
Step by step video & image solution for In the adjoining figure, AD and BE are the medians of triangle ABC and DF||BE. Show that CF=(1)/(4)AC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
47 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
9 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
In the given figure AD and BE are the medians of ΔABC and BE || DF . Prove that CF=1/4AC.
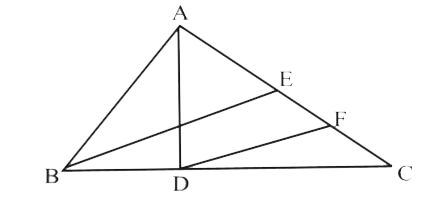
View SolutionIn the adjoining figure. AD and BE and BE are two medians of ΔANC.if DF||BE,then prove thatCG=14AC.
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
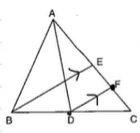
View SolutionIn the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionIn the given figure, BM and EN are respectively the medians of ΔABCandΔDEF. If ΔABC~ΔDEF, prove that:
(a) ΔAMB~ΔDNE
(b)ΔCMB~ΔFNE
( c) BMEN=ACDF

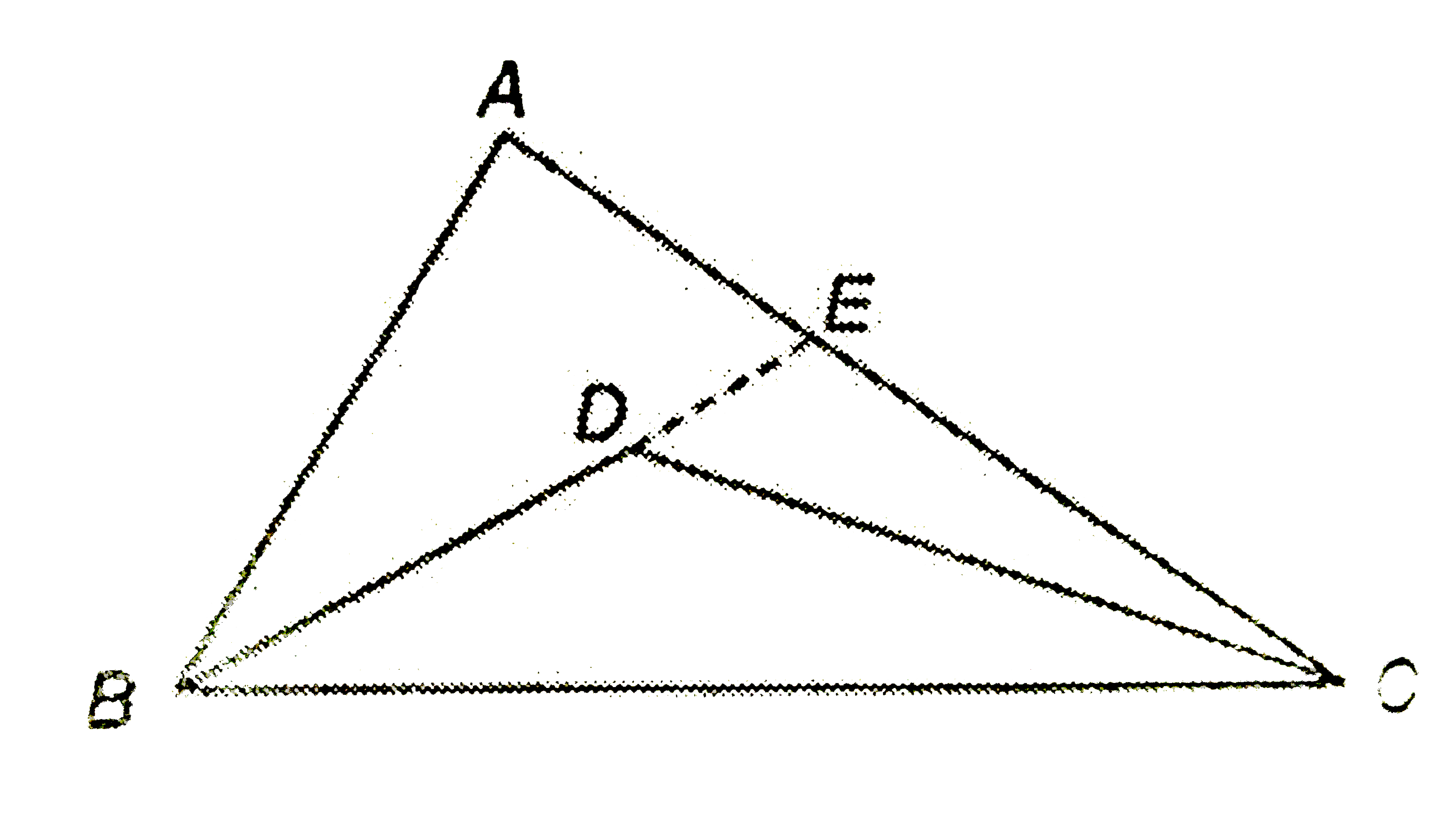
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that (BD+DC)<(AB+AC).
View SolutionIn the adjoining figure, AP⊥BC ,AD||BC ,then find A(ΔABC):A(ΔBCD) .
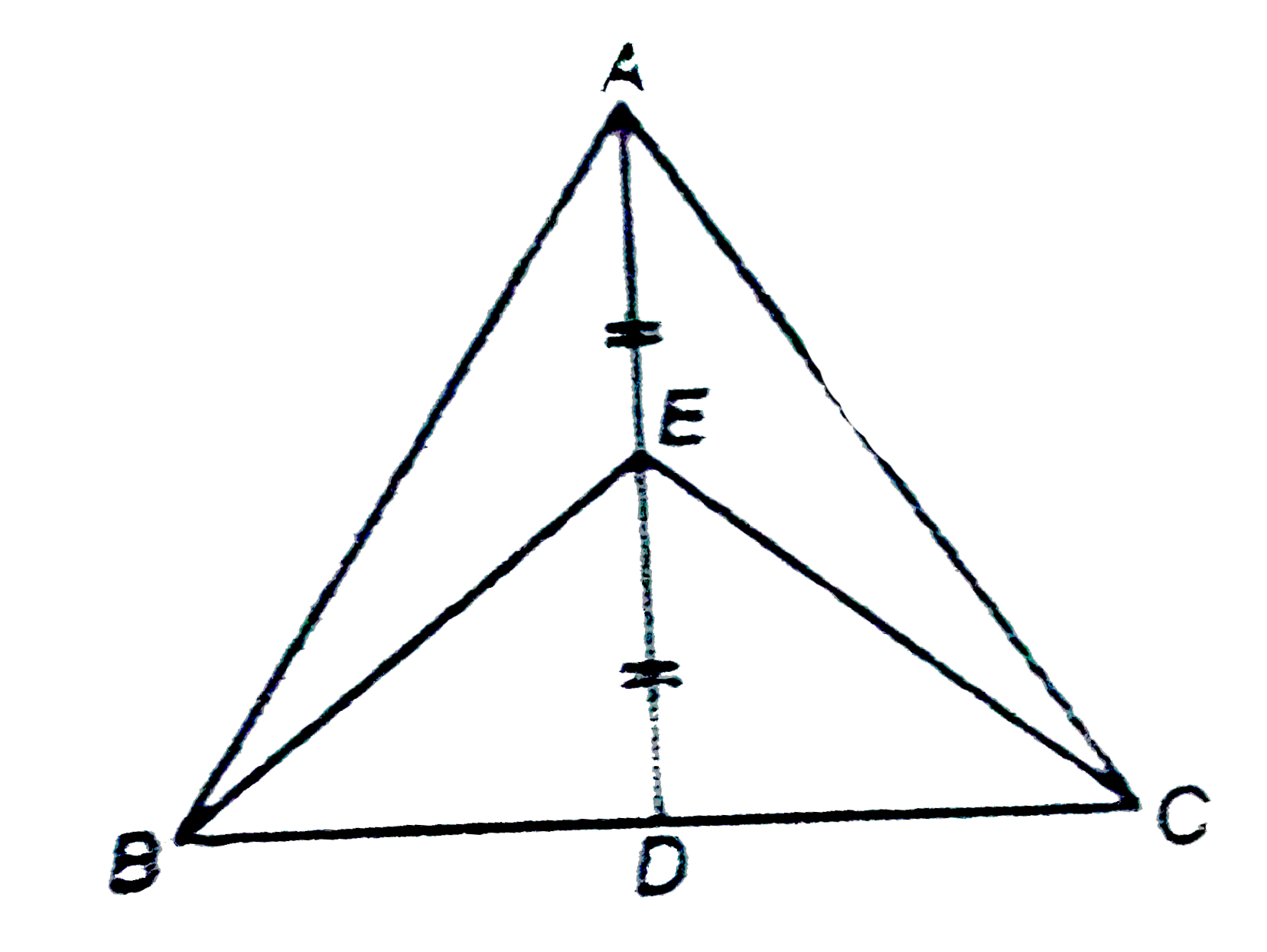
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View Solution
