In the given figure, ABCD is a cyclic quadrilateral . A circle passing through A and B, meets AD and BC in E and F respectively. Prove that EF∣∣DC.
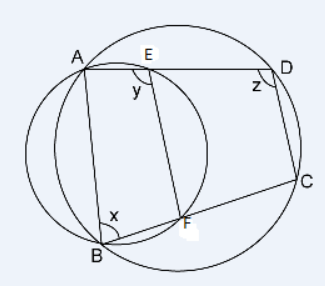
Join EF.
Now, ABFE being a cyclic quadrilateral, we have
∠1+∠2=180∘ …..(i)
Also, ABCD being a cyclic quadrilateral , we have
∠1+∠3=180∘ …....(ii)
From (i) and (ii) , we get
∠1+∠2=∠1+∠3⇒∠2=∠3
But, there are corresponding angles
∴EF∣∣DC
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
In Figure, ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EFDC
View SolutionIn figure, ABE is a in which AE=BE . Circle passing through A and B intersects AE and BE at D and C respectively. Prove that DC∣∣AB.
View SolutionAD is a median of △ABC. The bisectors of ∠ADBand∠ADC meets AB and AC in E and F respectively prove that EF||BC.
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View SolutionIn the given figure, ABCD is a quadrilateral in which AB∣∣DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB=CQ, (ii) DQ=DC+AB
View SolutionIn the given figure ABCD is a quadrilateral in which AB||DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i)AB=CQ,(ii)DQ=DC+AB.

View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionIn the given figure, ABCD is a parallelogram. E and F are the centroids of △ABD and △BCD, respectively.EF is equal to
View SolutionIn cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View Solution
