Let X be a discrete random variable whose probability distribution is defined as follows: P(X=x)={k(x+1)forx=1,2,3,42kxforx=5,6,70otherwise , where k is a constant. Find (i) k (ii) E(X) (iii) standard deviation of X.
To solve the problem, we will follow these steps:
Step 1: Find the constant k
The probability distribution is given as:
- P(X=x)=k(x+1) for x=1,2,3,4
- P(X=x)=2kx for x=5,6,7
- P(X=x)=0 otherwise
We need to ensure that the total probability sums to 1:
∑P(X=x)=1
Calculating the probabilities:
- For x=1: P(X=1)=k(1+1)=2k
- For x=2: P(X=2)=k(2+1)=3k
- For x=3: P(X=3)=k(3+1)=4k
- For x=4: P(X=4)=k(4+1)=5k
- For x=5: P(X=5)=2k(5)=10k
- For x=6: P(X=6)=2k(6)=12k
- For x=7: P(X=7)=2k(7)=14k
Now summing these probabilities:
2k+3k+4k+5k+10k+12k+14k=50k
Setting this equal to 1:
50k=1⟹k=150
Step 2: Find E(X)
The expected value E(X) is calculated as:
E(X)=∑x⋅P(X=x)
Calculating each term:
E(X)=1⋅(2k)+2⋅(3k)+3⋅(4k)+4⋅(5k)+5⋅(10k)+6⋅(12k)+7⋅(14k)
Substituting k=150:
E(X)=2k+6k+12k+20k+50k+72k+98k
=k(2+6+12+20+50+72+98)=k⋅260
=26050=265=5.2
Step 3: Find the variance Var(X)
The variance is given by:
Var(X)=E(X2)−(E(X))2
First, we calculate E(X2):
E(X2)=∑x2⋅P(X=x)
Calculating each term:
E(X2)=12⋅(2k)+22⋅(3k)+32⋅(4k)+42⋅(5k)+52⋅(10k)+62⋅(12k)+72⋅(14k)
Substituting k=150:
E(X2)=2k+12k+36k+80k+250k+432k+686k
=k(2+12+36+80+250+432+686)=k⋅1498
=149850=29.96
Now we can find the variance:
Var(X)=E(X2)−(E(X))2=29.96−(5.2)2
Calculating (5.2)2=27.04:
Var(X)=29.96−27.04=2.92
Step 4: Find the standard deviation σ
The standard deviation is the square root of the variance:
σ=√Var(X)=√2.92≈1.71
Final Answers:
(i) k=150
(ii) E(X)=5.2
(iii) Standard deviation σ≈1.71
---
- P(X=x)=k(x+1) for x=1,2,3,4
- P(X=x)=2kx for x=5,6,7
- P(X=x)=0 otherwise
∑P(X=x)=1
- For x=1: P(X=1)=k(1+1)=2k
- For x=2: P(X=2)=k(2+1)=3k
- For x=3: P(X=3)=k(3+1)=4k
- For x=4: P(X=4)=k(4+1)=5k
- For x=5: P(X=5)=2k(5)=10k
- For x=6: P(X=6)=2k(6)=12k
- For x=7: P(X=7)=2k(7)=14k
2k+3k+4k+5k+10k+12k+14k=50k
Setting this equal to 1:
50k=1⟹k=150
E(X)=∑x⋅P(X=x)
E(X)=1⋅(2k)+2⋅(3k)+3⋅(4k)+4⋅(5k)+5⋅(10k)+6⋅(12k)+7⋅(14k)
Substituting k=150:
E(X)=2k+6k+12k+20k+50k+72k+98k
=k(2+6+12+20+50+72+98)=k⋅260
=26050=265=5.2
Var(X)=E(X2)−(E(X))2
E(X2)=∑x2⋅P(X=x)
Calculating each term:
E(X2)=12⋅(2k)+22⋅(3k)+32⋅(4k)+42⋅(5k)+52⋅(10k)+62⋅(12k)+72⋅(14k)
Substituting k=150:
E(X2)=2k+12k+36k+80k+250k+432k+686k
=k(2+12+36+80+250+432+686)=k⋅1498
=149850=29.96
Var(X)=E(X2)−(E(X))2=29.96−(5.2)2
Calculating (5.2)2=27.04:
Var(X)=29.96−27.04=2.92
σ=√Var(X)=√2.92≈1.71
(i) k=150
Topper's Solved these Questions
Similar Questions
The probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution as given below
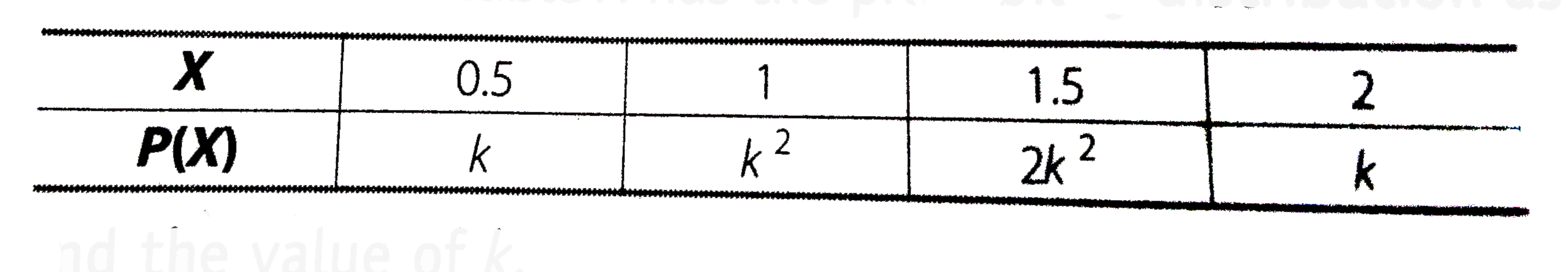
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution as given below
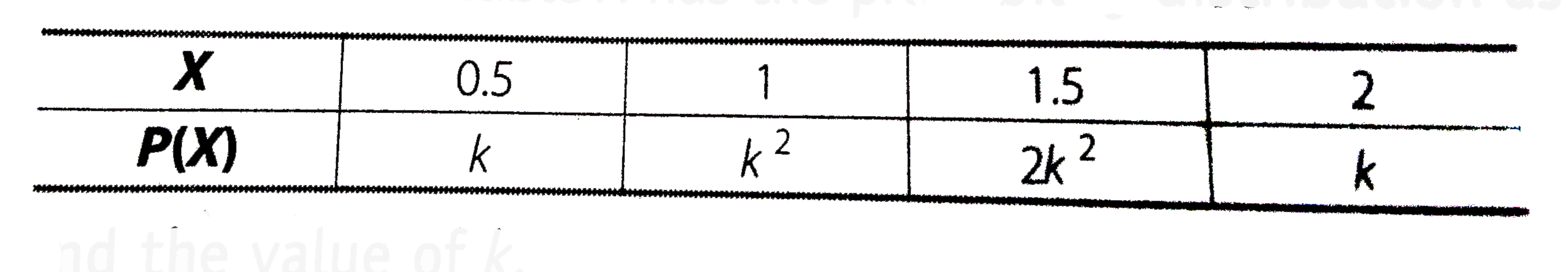
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
View SolutionThe probability distribution for a random variable X is as follows:
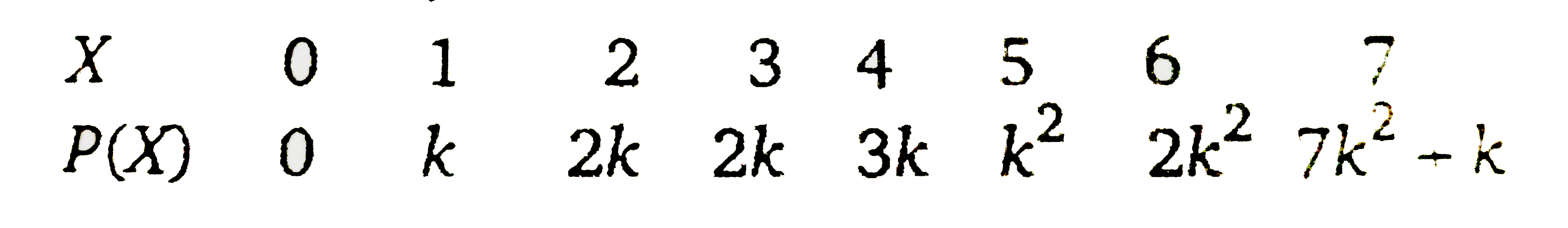
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
