The larger of the area bounded by y = cosx, y = x + 1 and y = 0 is
A
12 sq unit
B
32 sq units
C
1 sq unit
D
2 sq units
Video Solution
Text Solution
The correct Answer is:B
y = cos x and y = x + 1 meet at the point
(0,1), y = x + 1 passes through the points (-1,0) and [0,1], y=cosx meets X-axis at (−π2,0)and(π2,0).
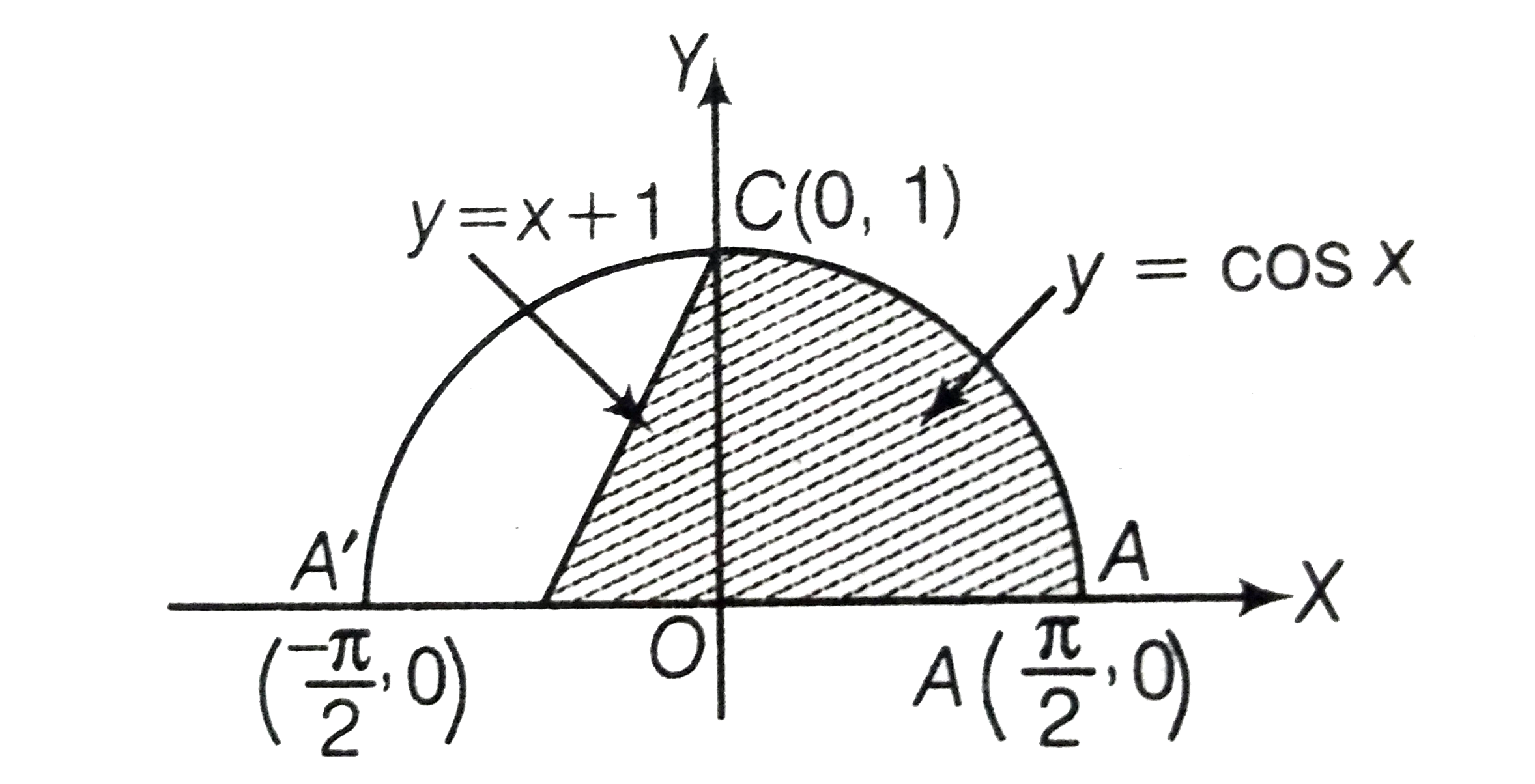
∴ Required area =∫0−1(x+1)dx+∫π/20cosxdx
=[x22+x]0−1+[sinx]π/20
=0−(12−1)+1=32 sq units.
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
The area bounded by the curves x + 2|y| = 1 and x = 0 is
A14B12C1D2The area of the region bounded by y = x - 1 and x=3−y2 is
A52B72C92D4The area of the region bounded by y=2cosx,y=3tanx and the y-axis is
A1+32log3−log2Blog32C1+3log2√3D1+32log3−log8
Find the area of the region bounded by y=sinx,y=cosx and ordinates x=0,x=π/2.
View SolutionThe area bounded by y=4−x2,y=0andy=3 is
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 b. 2 c. 2√2 d. 4
View SolutionThe area bounded by y=cosx, y=0 and |x|=1 is given by
View SolutionThe area bounded by y-1 = |x|, y = 0 and |x|=12 will be :
View Solution
