The line x=π4 divides the area of the region bounded by y = sin x, y = cos x and X-axis (0≤x≤π2) into two regions of areas A1 and A2. Then, A1:A2 equals
A
4:1
B
3:1
C
2:1
D
1:1
Video Solution
Text Solution
The correct Answer is:D
Area, A1=∫π/40sinxdx
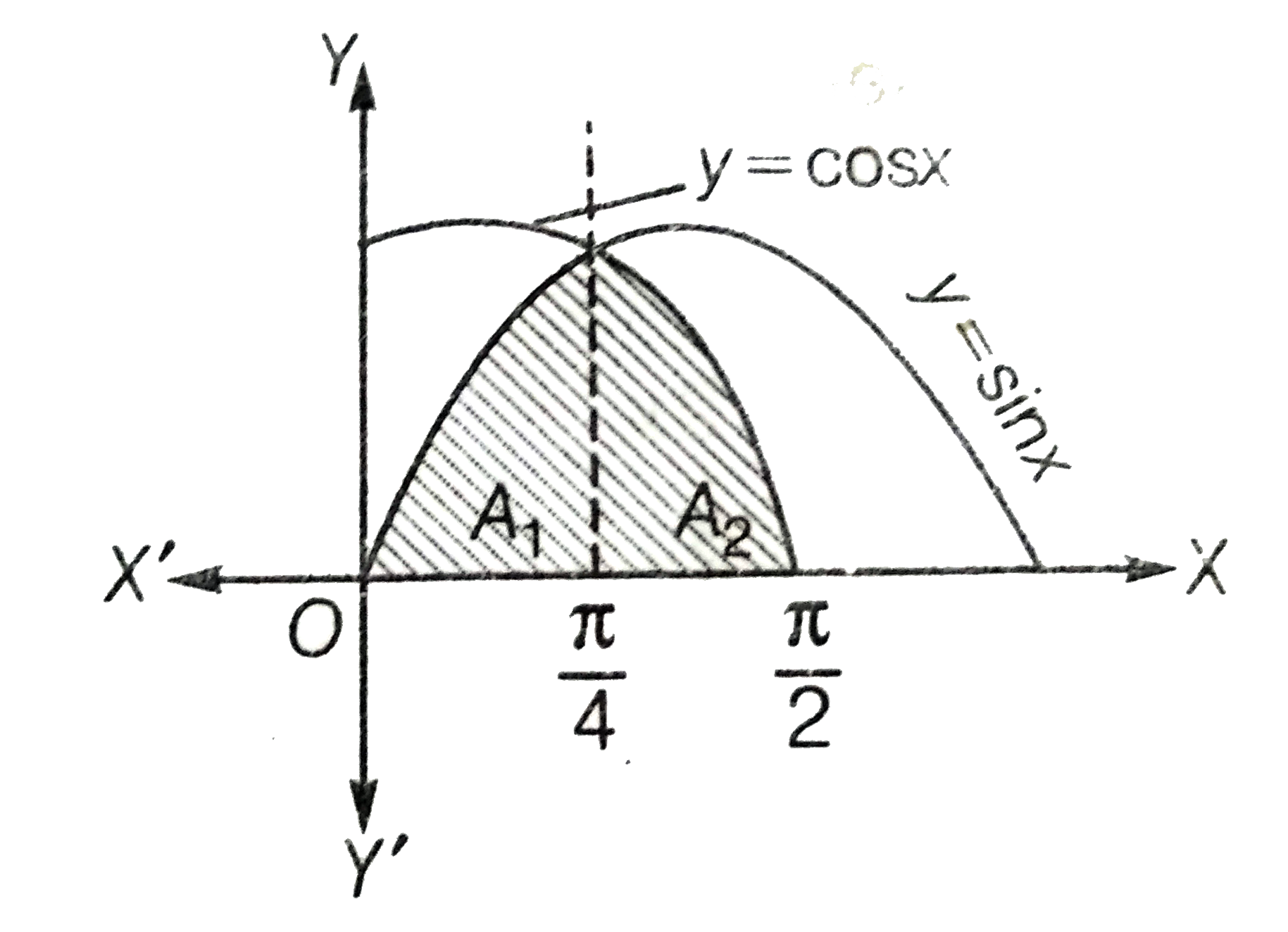
=−[cosx]π/40=1−1√2=√2−1√2
and area, A2=∫π/2π/4cosxdx=[sinx]π/2π/4=[1−1√2]=√2−1√2
∴A1:A2=√2−1√2:√2−1√2=1:1
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the y-axis, y=cosxandy=sinx,0≤x≤π2 is:
A√2 sq. unitsB(√2+1) sq. unitsC√2(√2−1) sq. unitsD(2√2−1) sq. unitsThe area of the region bounded by the y-axis, y = cos x and y = sin x,0≤x≤π/2 is
A√2 sq. unitsB(√2+1) sq. unitsC(√2−1) sq. uintsD(2√2−1) sq. unitsThe area of the region bounded by the curve y=xsinx, x-axis, x=0 and x=2π is :
A2π sq. unitsB3π sq. unitsC4π sq. unitsD5π sq. units
Find the area of the region bounded by the curve y = sin x, the X−axis and the given lines x=−π,x=π
View SolutionIf the line x−1=0 divides the area bounded by the curves 2x+1=√4y+1,y=xandy=2 in two regions of area A1andA2(A1<A2), then (A−21−A−22) is equal to
View SolutionThe parabola y2=4x+1 divides the disc x2+y2≤1 into two regions with areas A1 and A2. Then |A1−A2| equal
View SolutionThe area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x=2π is
View SolutionThe area of the region bounded by the curve y = sin x between the ordinates x=0,x=π2 and the X-axis is
View Solution
