Complete Solutions to EXERCISE 18(A) of chapter TANGENTS AND INTERSECTING CHORDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TANGENTS AND INTERSECTING CHORDS |
| SELINA PUBLICATION | EXERCISE 18(A) |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point oat a distance of 10 cm from its centre.
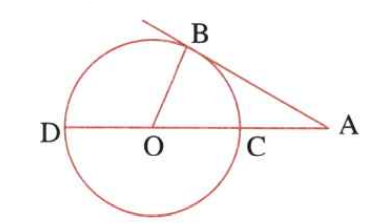
View SolutionIn the given figure, O is the centre of the circle ans AB is a tangent at B. If AB=15 cm and AC=7.5cm, calculate the radius of the circle.
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
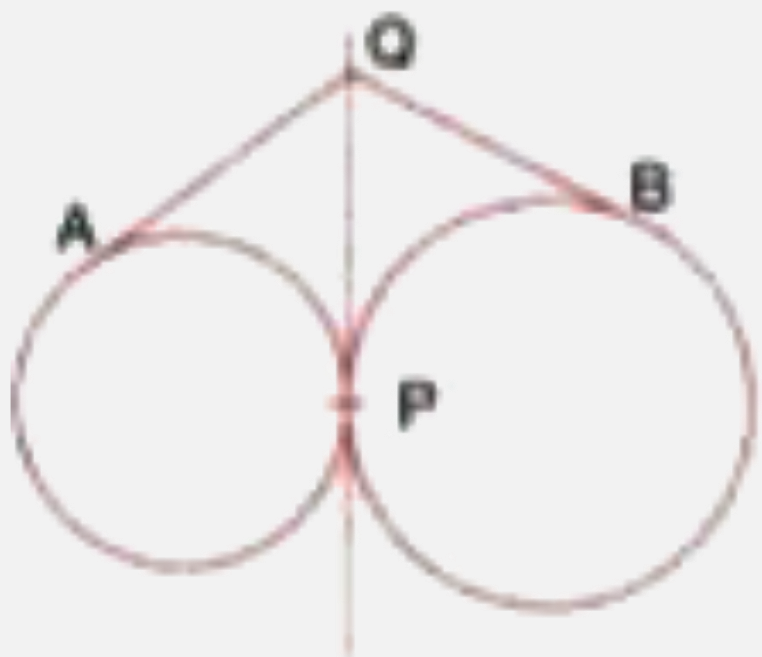
View SolutionTwo circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionThree circles touch each other externally. A triangle is formed when the centres of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
View SolutionA quadrilateral ABCD is ABCD is drawn to circumscribe a circle. Prove that
`AB+CD=BC+AD`
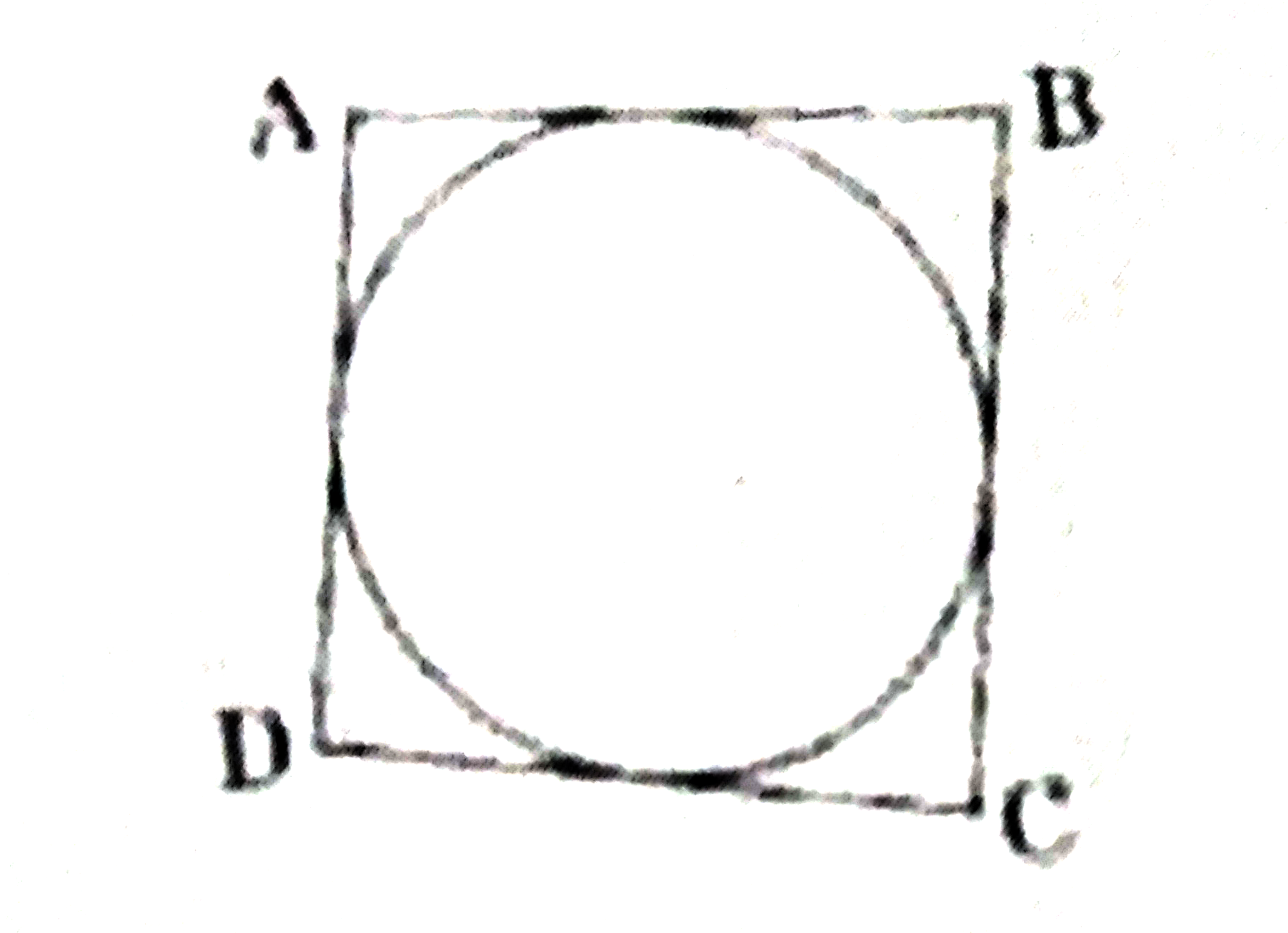
View SolutionIf the sides of a parallelogram touch a circle prove that the parallelogram is a rhombus.
View SolutionFrom the given figure, prove that :
`AP+BQ+CR=BP+CQ+AR`
Also show that
`AP+BQ+CR=1/2xx"Perimeter of " DeltaABC`.
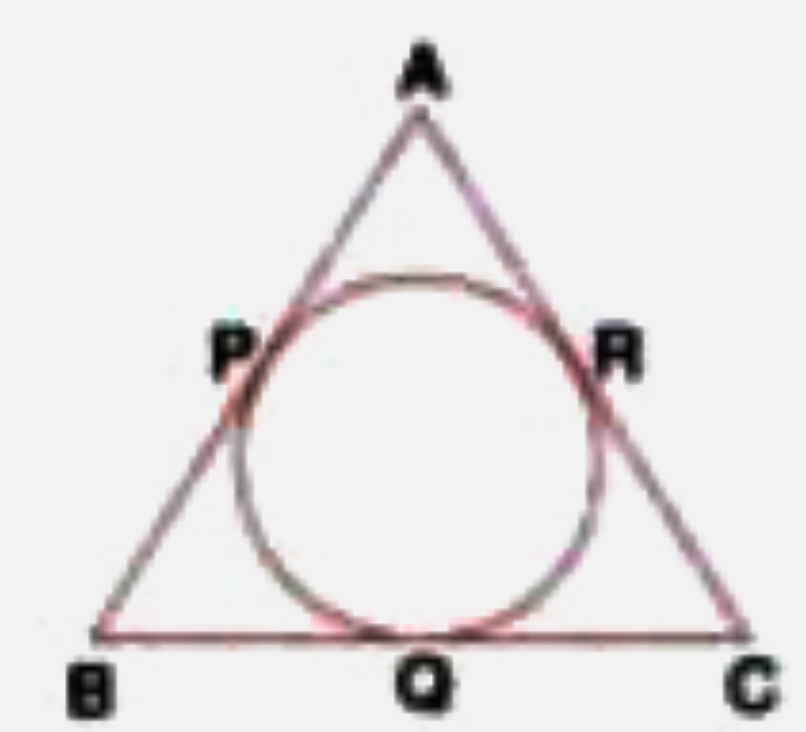
View SolutionIn the figure if AB=AC then prove that `BR=CR`

View SolutionRadii of two circles are 6.3 cm and 3.6 cm. State the distance between their centres if
(i) they touch each other externally,
(ii) They touch each other internally.
View SolutionFrom a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) `/_AOP=/_BOP`
(ii) `OP` is the `_|_` bisector of chord AB.
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
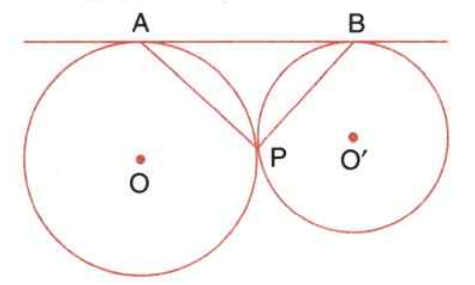
(i) tangent at point P bisects AB
(ii) angle `APB=90^(@)`
View SolutionTangents AP and AQ are drawn to a circle, with centre O, from an exterior point A.
Porve that :
`/_PAQ=2/_OPQ`
View SolutionTwo parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
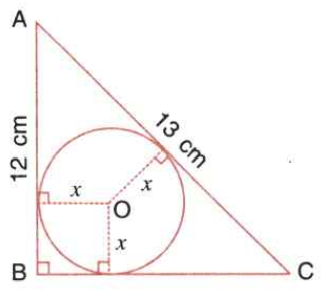
View SolutionIn a triangle ABC, the incircle (centre O) touches BC , CA and AB at points P,Q and R respectively. Calculate:
(i) `/_QOR` (ii) `/_QPR`
given that `/_A=60^(@)`
View SolutionIn the following figure PQ and PR are tangents to the circle with the centre O. If `angleQPR = 60^(@)` calculate
(i)`angleQOR`
(ii) `angleOQR`
(iii) `angleQSR`
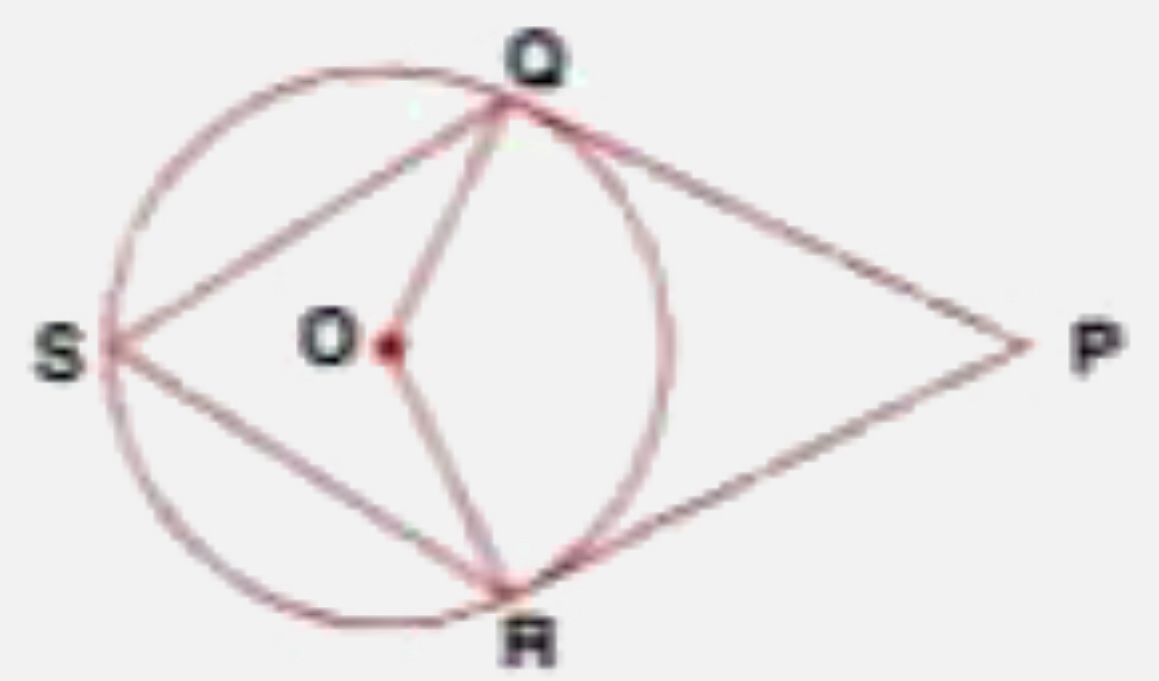
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
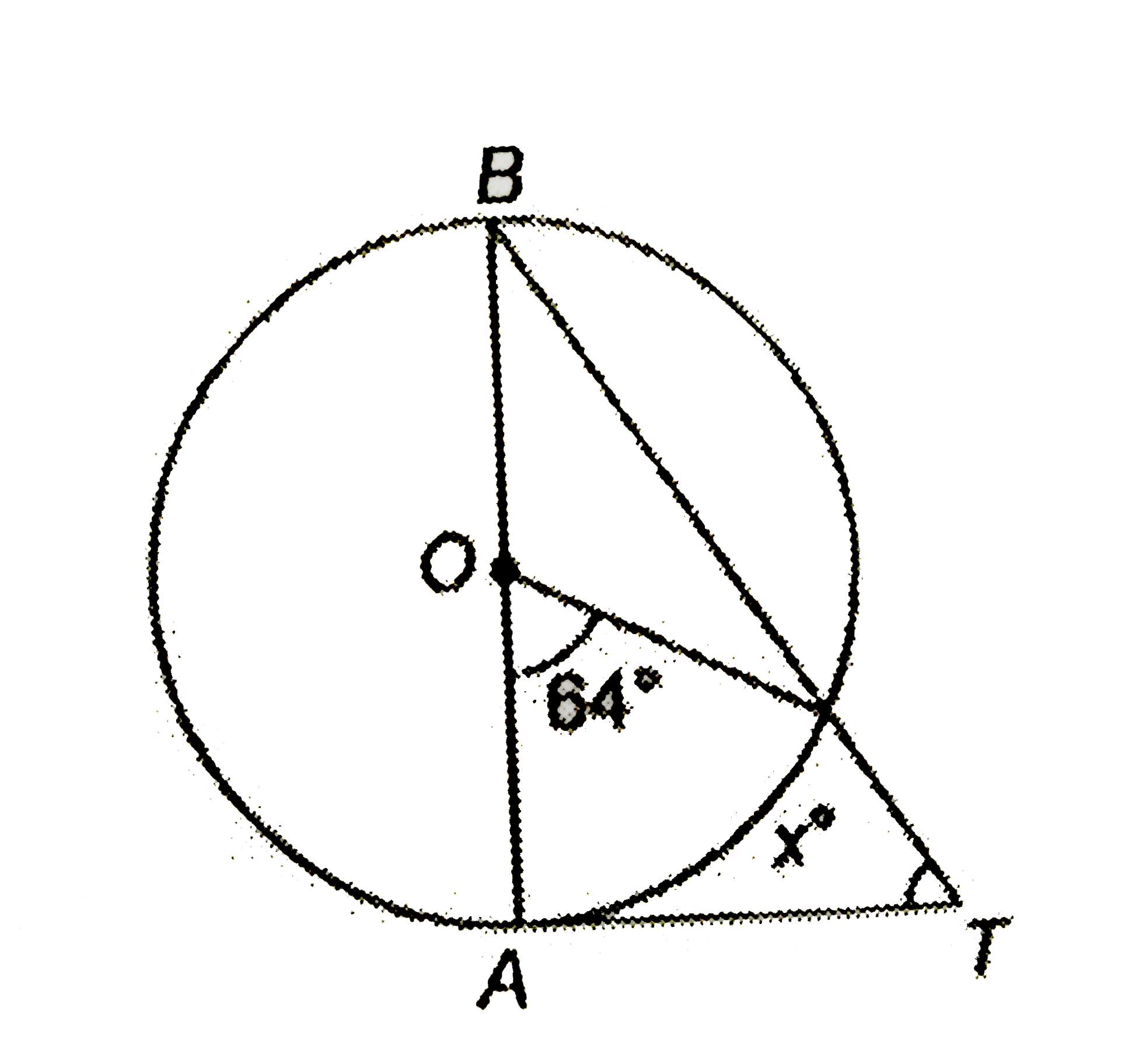
View SolutionIn quadrilateral ABCD angled `D=90^(@)`, BC=38cm and DC=25cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27cm. Find the radius of the circle.
View SolutionIn the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given `/_SPR=x^(@)` and `/_QRP=y^(@)`,
prove that
(i) `/_ORS=y^(@)`
ii. Write an expression connecting x and y.
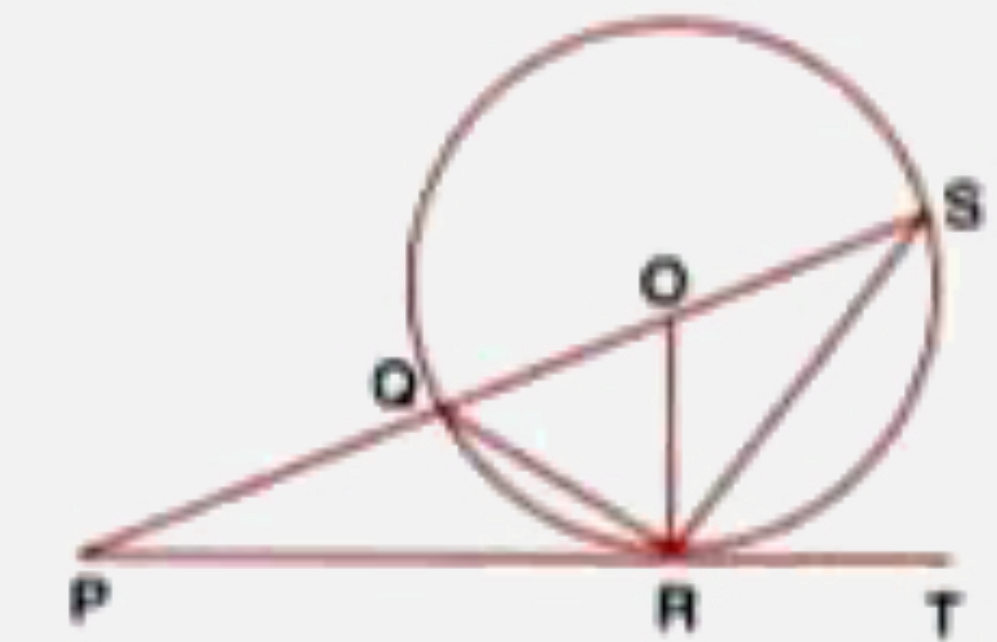
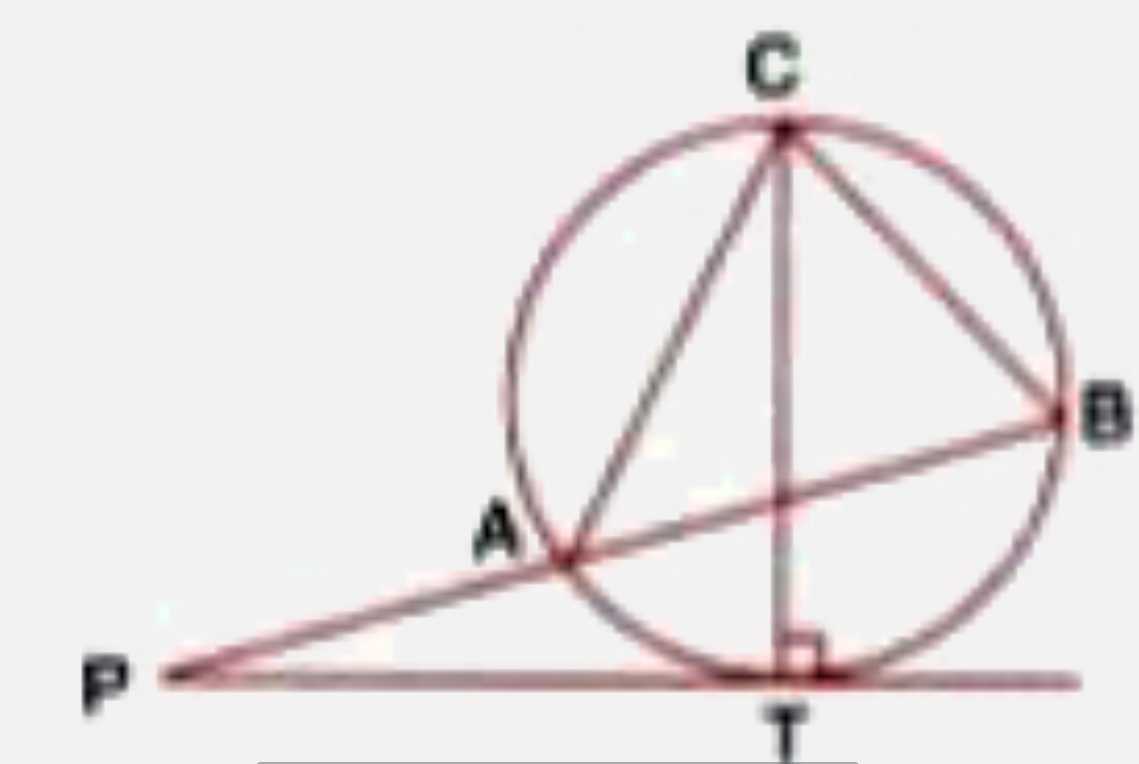
View SolutionPT is a tangent to the circle at T.
If `/_ABC=70^(@)` and `/_ACB=50^(@)`, calculate:
(i) `/_CBT`
(ii) `/_BAT`
(iii) `/_APT`
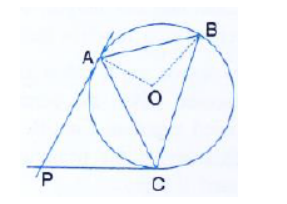
View SolutionIn the given figure, O is the centre of the circumcircle of `triangleABC`. Tangents at A and C intersect at P. Given angle `AOB=140^(@)` and angle `APC=80^(@)` find the angle BAC.
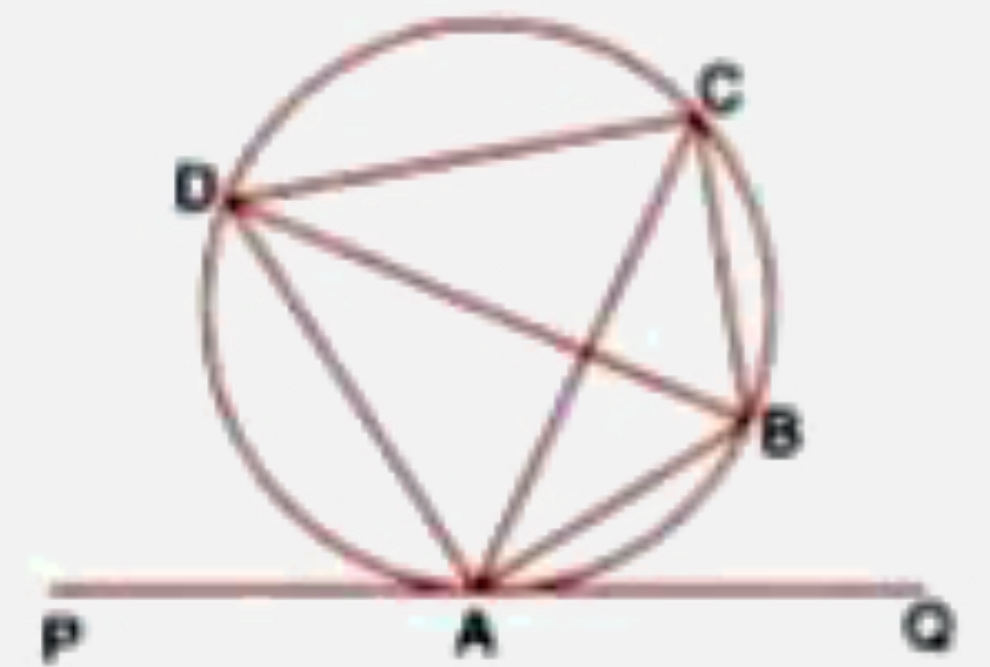
View SolutionIn the given PQ is a tangent to the circle at A. AB and AD are bisectors of `/_CAQ` and `/_PAC`. If `/_BAQ=30^(@)`, prove that: BD is diameter of the circle.
View Solution
EXERCISE 18(A) questions and complete solutions for chapter TANGENTS AND INTERSECTING CHORDS of SELINA MATHS (ENGLISH) of Class 10