Complete Solutions to EXERCISE 18 (B) of chapter TANGENTS AND INTERSECTING CHORDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TANGENTS AND INTERSECTING CHORDS |
| SELINA PUBLICATION | EXERCISE 18 (B) |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
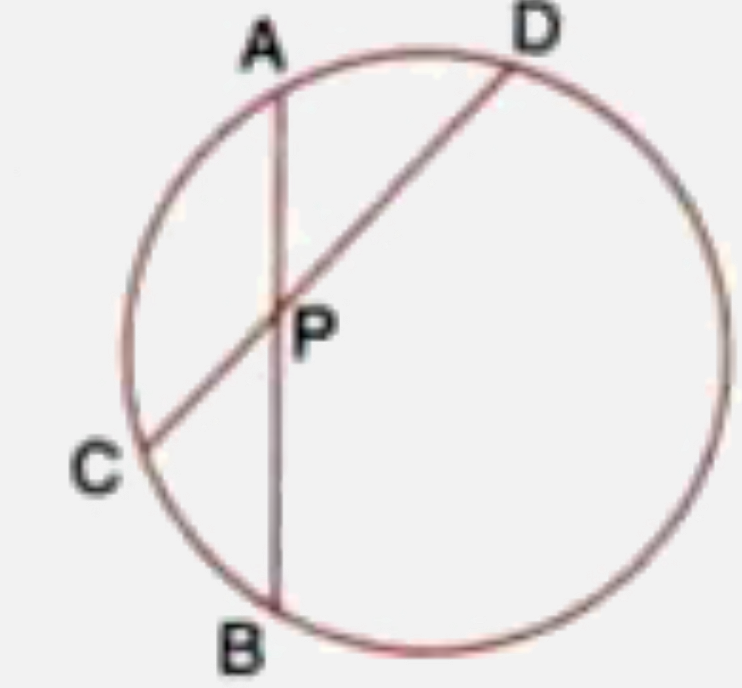
In the given figure
`3xxCP=PD=9cm`
and AP=4.5 cm.
Find BP.
View SolutionIn the given figure `5X PA=3X AB=30cm`
and PC=4 cm
Find CD.
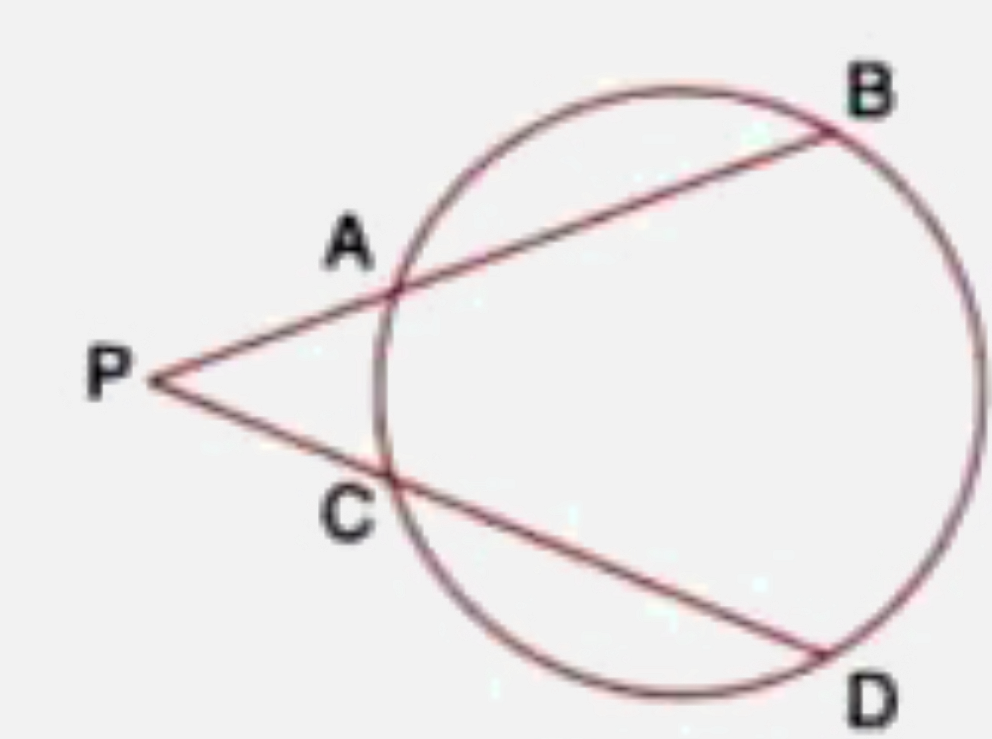
View SolutionIn the given figure
tangent PT=12.5 cm and PA=10cm, find AB.

View SolutionIn the given figure diameter AB and chord CD of a circle meet at P.PT is a tangent to
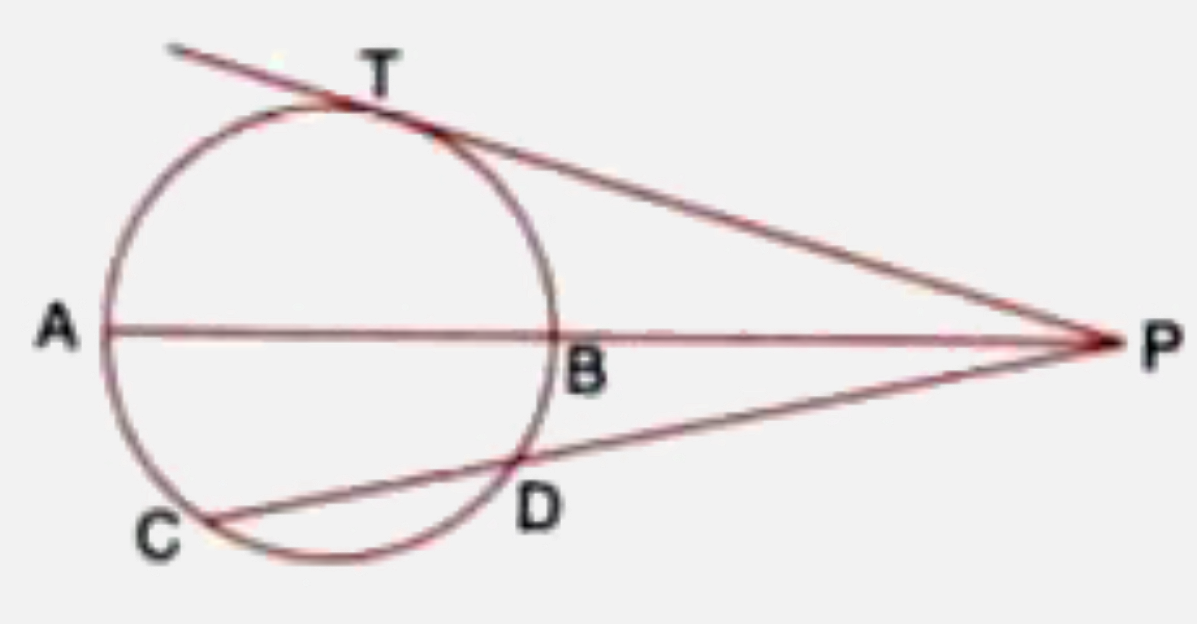
the circle at T.CD=7.8 cm, PD=5 cm, PB=4 cm. Find :
(i) AB (ii) the length of tangent PT.
View SolutionIn the following figure PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If `/_ADB=30^(@)` and `/_CBD=60^(@)`. Calculate :

(i) `/_QAB`
(ii) `/_PAD`
(iii) `/_CDB`
View SolutionIf PQ is a tangent to the circle at R calculate
(i) `/_PRS`
(i) `/_ROT`
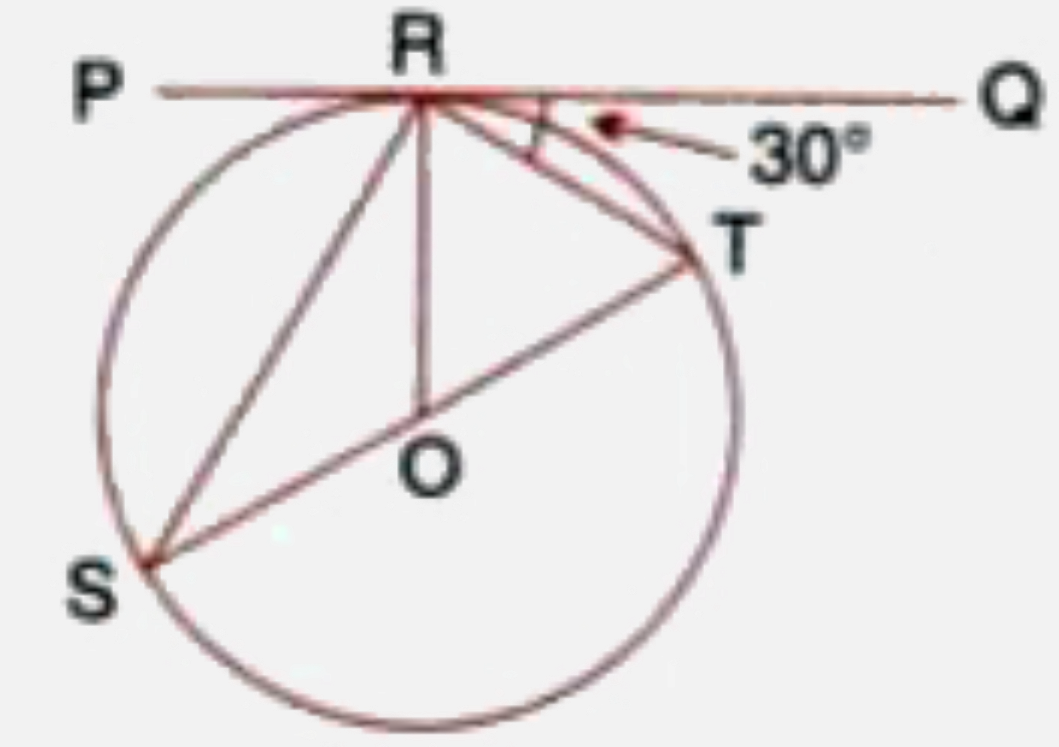
Given O is the centre of the circle and angle `TRQ=30^(@)`
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle `BAC=30^(@)`. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionTangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR show that `Delta PQR` is isosceles.
View SolutionTwo circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.

View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove `/_CPA cong /_DPB`.
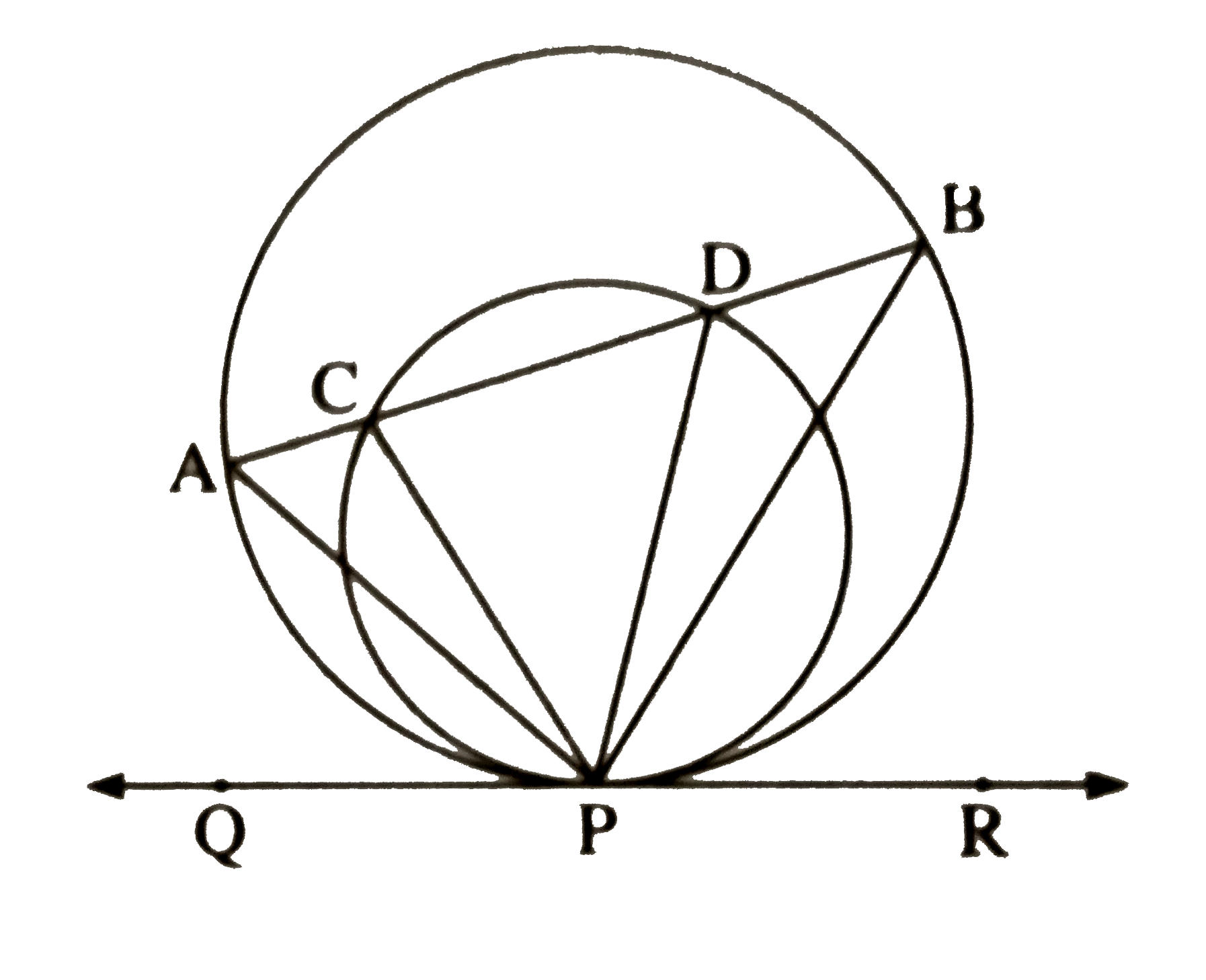
View SolutionIn a cyclic quadrilateral ABCD the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
View SolutionIn the figure ABCD is a cyclic quadrilateral with BC=CD. TC is tangent to the circle at point C and DC is produced to point G. If `/_BCG=108^(@)` and O is the centre of the circle find
(i) angle BCT
(ii) angle DOC

View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionIn the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
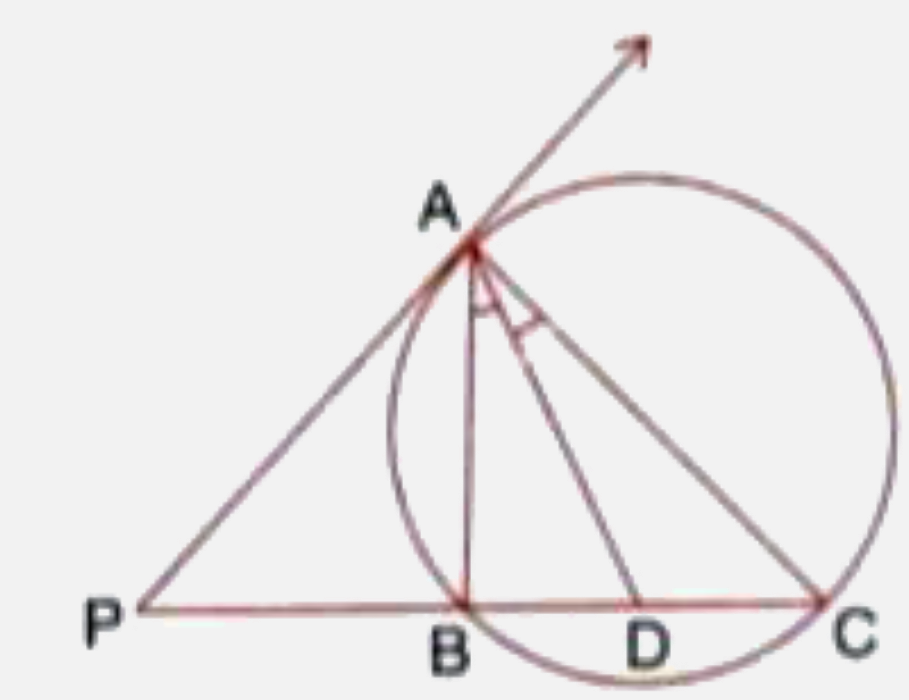
`/_CAD=1/2[/_PBA-/_PAB]`
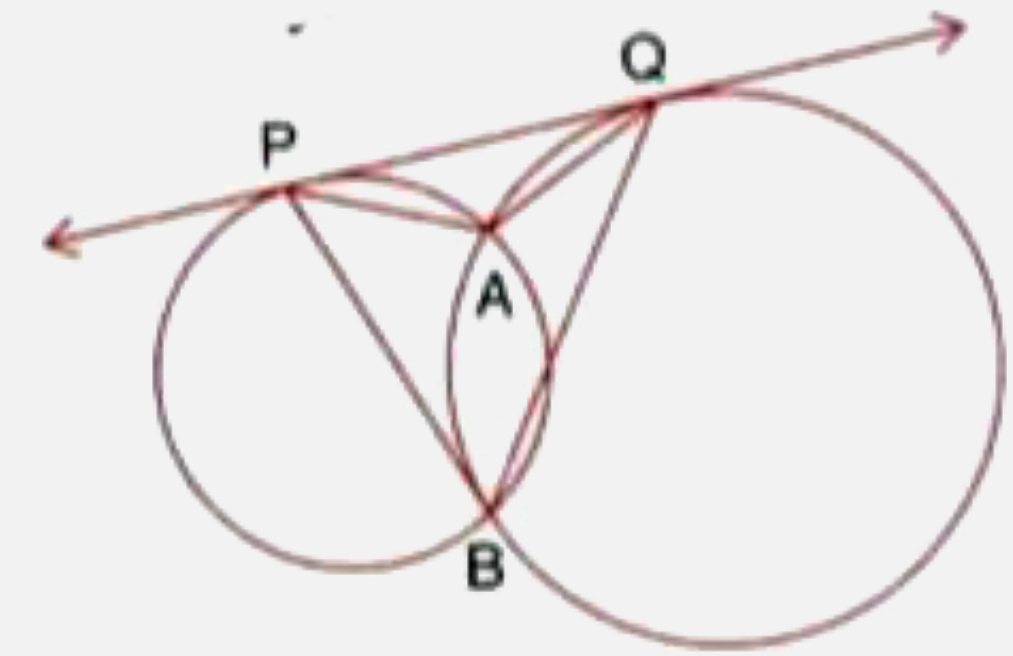
View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
View SolutionIn the figure chords AE and BC intersect each other at point D
(i) If `/_CDE=90^(@)`
AB=5cm
BD=4cm and CD=9 cm
find DE
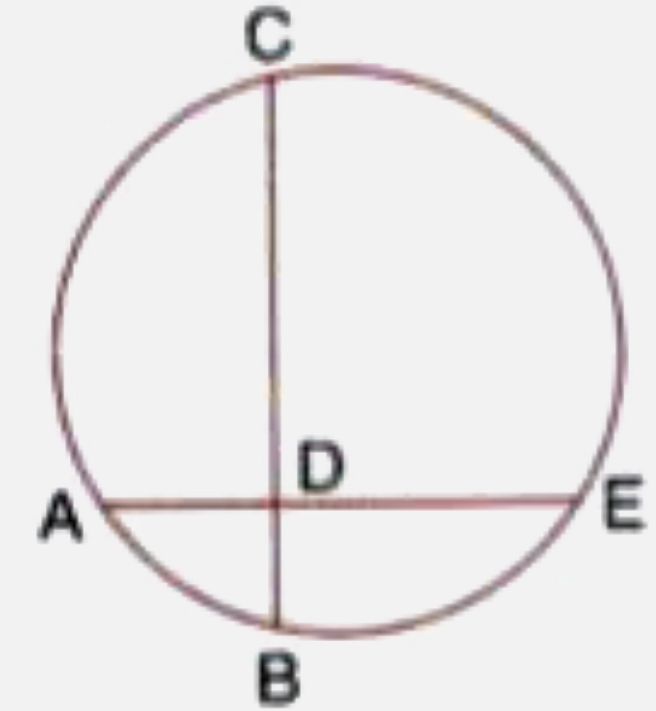
(ii) If AD=BD, show that AE=BC
View SolutionCircles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
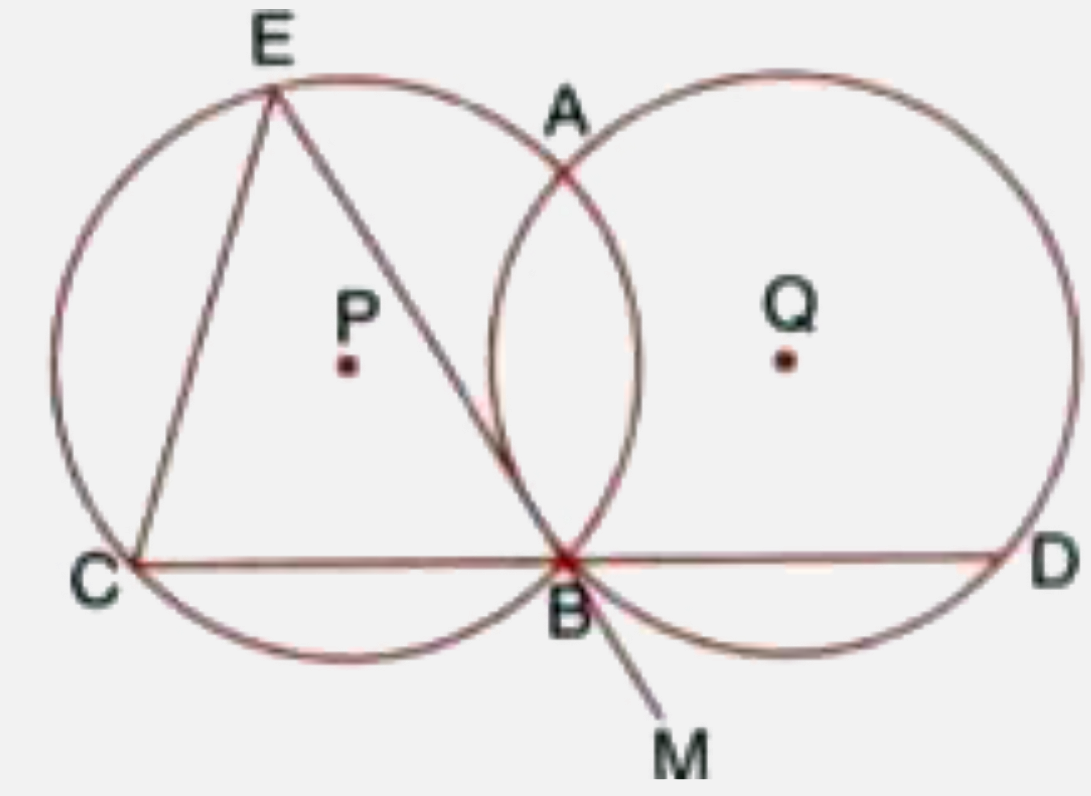
View SolutionIn the adjoining figvure O is the centre of the circle and AB is a tangent to it at point B.
`/_BDC=65^(@)`. Find `/_BAO`
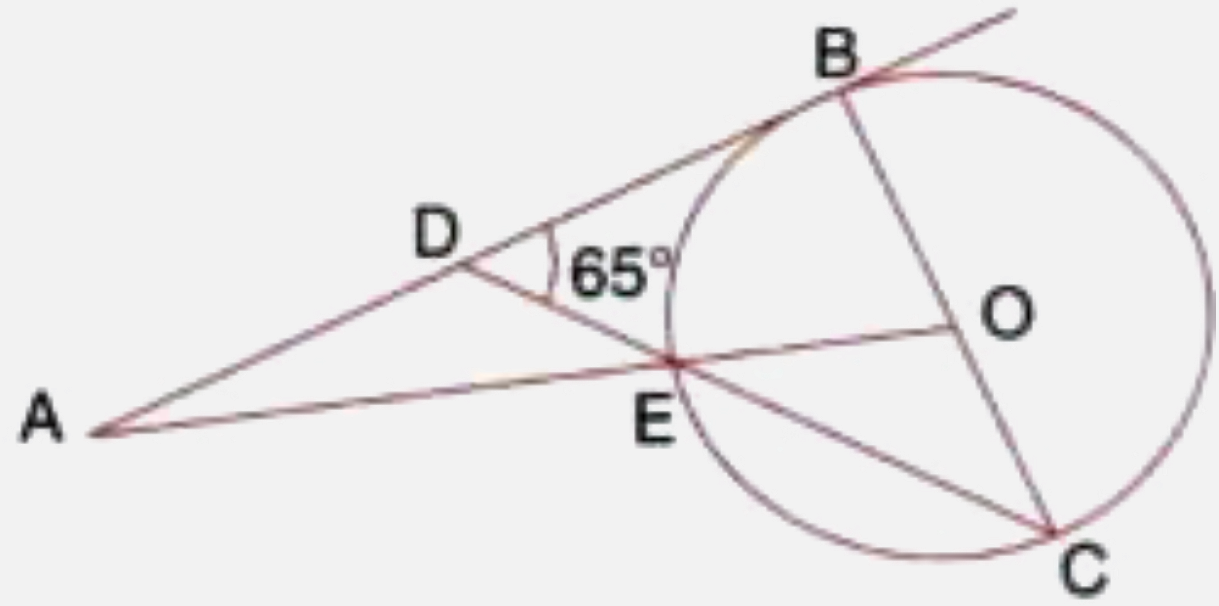
View Solution
EXERCISE 18 (B) questions and complete solutions for chapter TANGENTS AND INTERSECTING CHORDS of SELINA MATHS (ENGLISH) of Class 10