Complete Solutions to QUESTIONS of chapter TANGENTS AND INTERSECTING CHORDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TANGENTS AND INTERSECTING CHORDS |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
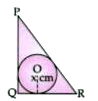
In triangle PQR, PQ = 24 cm, QR = 7 cm and `anglePQR=90^(@)`. Find the radius of the inscribed circle.
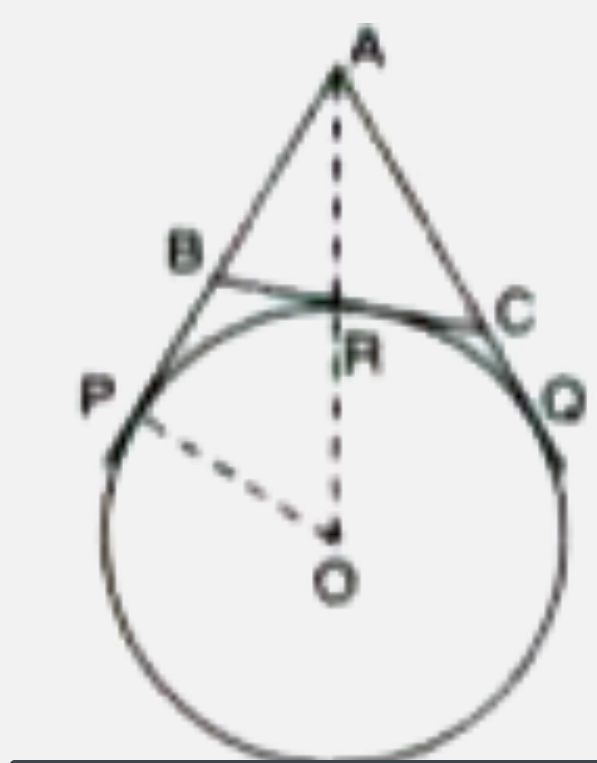
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
View SolutionA,B and C are three points on a circle. The tagent at C meets BA produced at T. Given thate `/+ATC=36^(@)` and that `/_ACT=48^(@)`, calculate the angle subtended by AB at the centre of the circle.

View SolutionP and Q are centres of circles of radii 9 cm and 2 cm respectively. PQ = 17 cm. R is the centre of a circle of radius x cm which touches the above circles externally. Given that `anglePRQ = 90^@` , write an equation in x and solve it.
View SolutionTwo circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
View SolutionThe centres of two circles with radii 6 cm and 2 cm are 10 cm apart. Calculate the length of the transverse common tangent.
View SolutionIn the figure given alongside PQ=QR, `/_RQP=68^(@)`, PC and QC are tangents to the circle with centre O. Calculate the values of (i) `/_QOP` (ii) `/_QCP`.

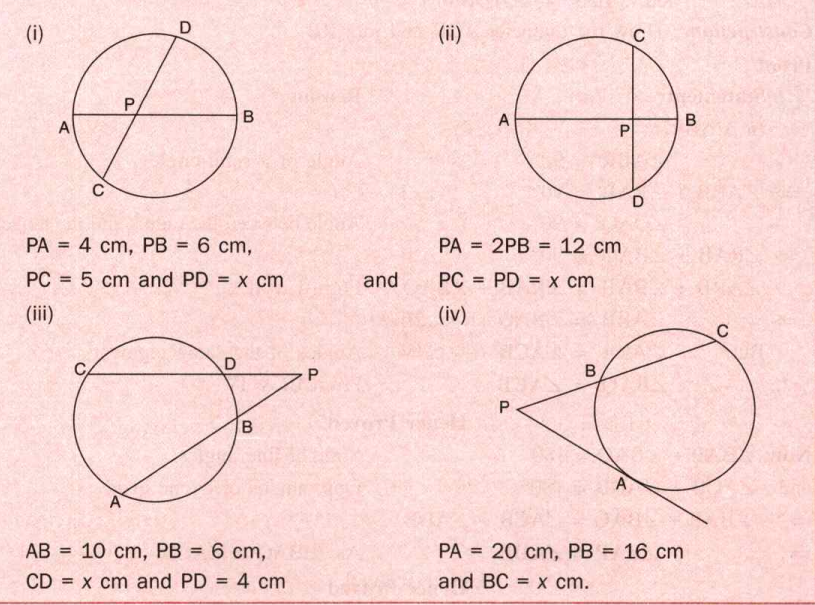
View SolutionFrom each of the folloiwng figures, find the value of x.
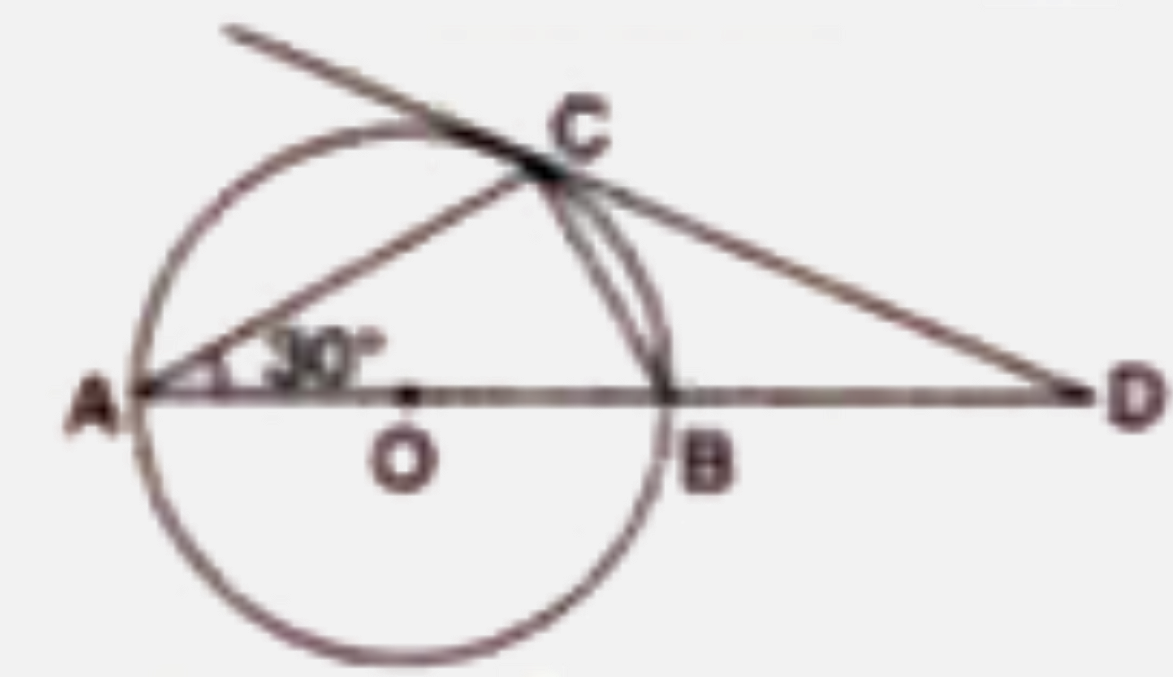
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that `/_BAC=30^(@)`. The tangent at C intersects AB produced at D. Prove that :BC=BD.
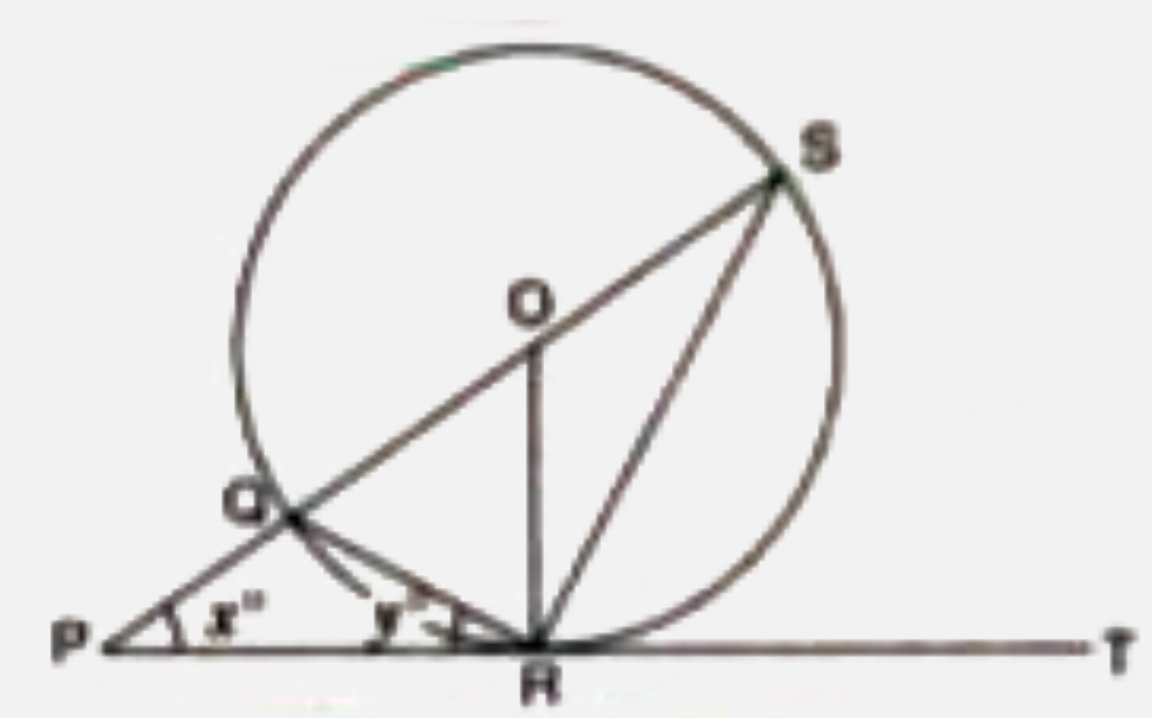
View SolutionIn the given figure PT touches a circle with centre O at R. Diameter SQ when produced meets PT at P. If `/_SPR=x^(@)` and `/_QRP=y^(@)`, show what `x^(@)+2y^(@)=90^(@)`
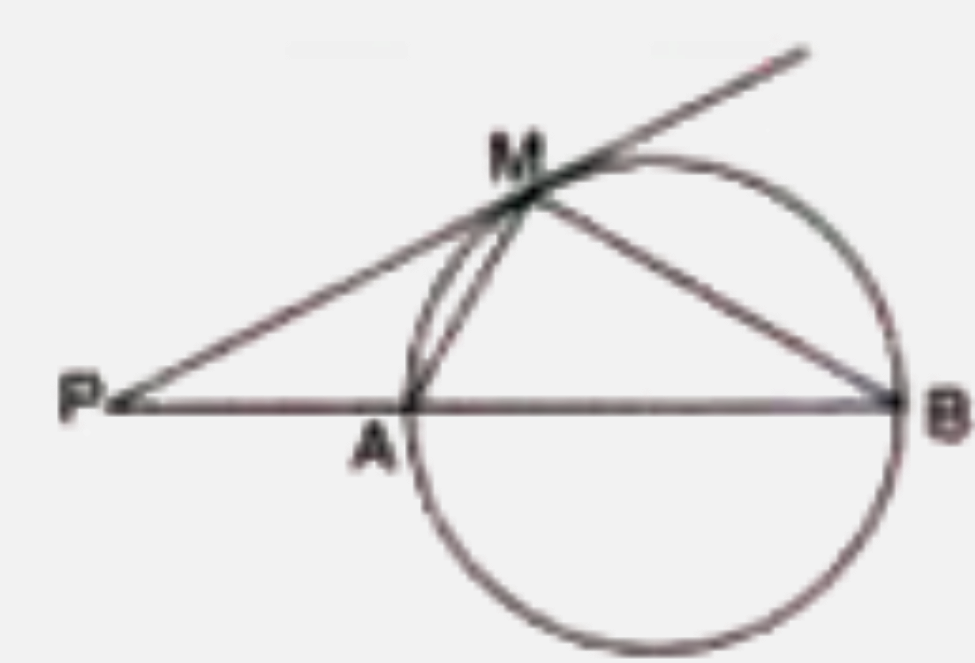
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) `DeltaPMB` is isosceles
(ii) `PAXxPB=MB^(2)`
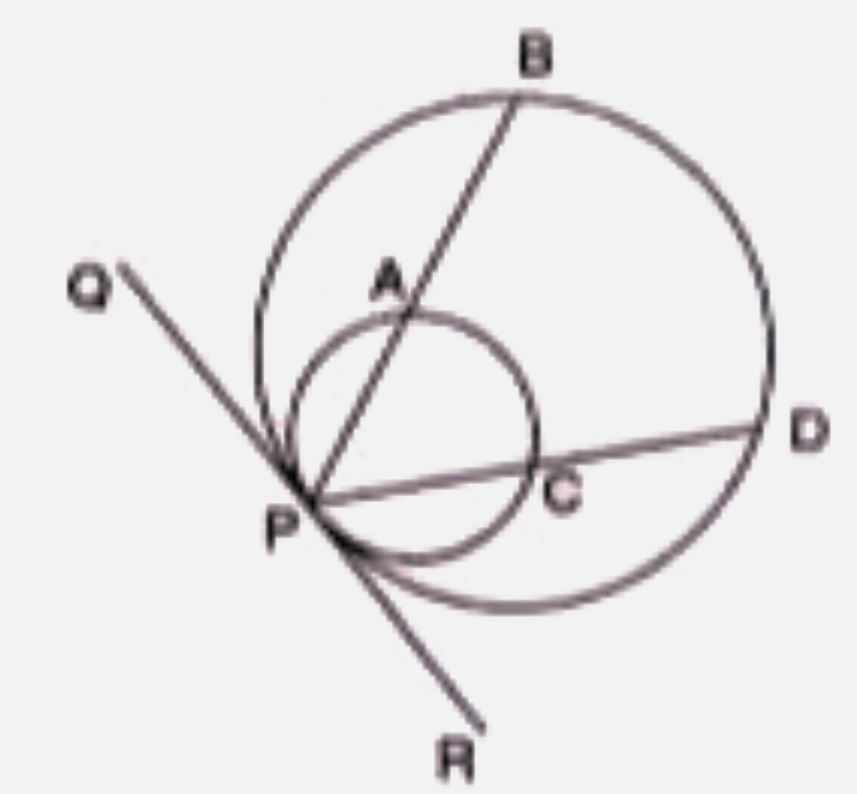
View SolutionTwo circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure.
Show that chord AC is parallel to chord BD.
View SolutionIn a right triangle ABC, a circle with AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent at P, bisects the side BC.
View SolutionABC is an isosceles trianlge with AB=AC. A circle through B touches side AC at its middle point D and intersects side AB in point P. Show that `AB=4xxAP`.
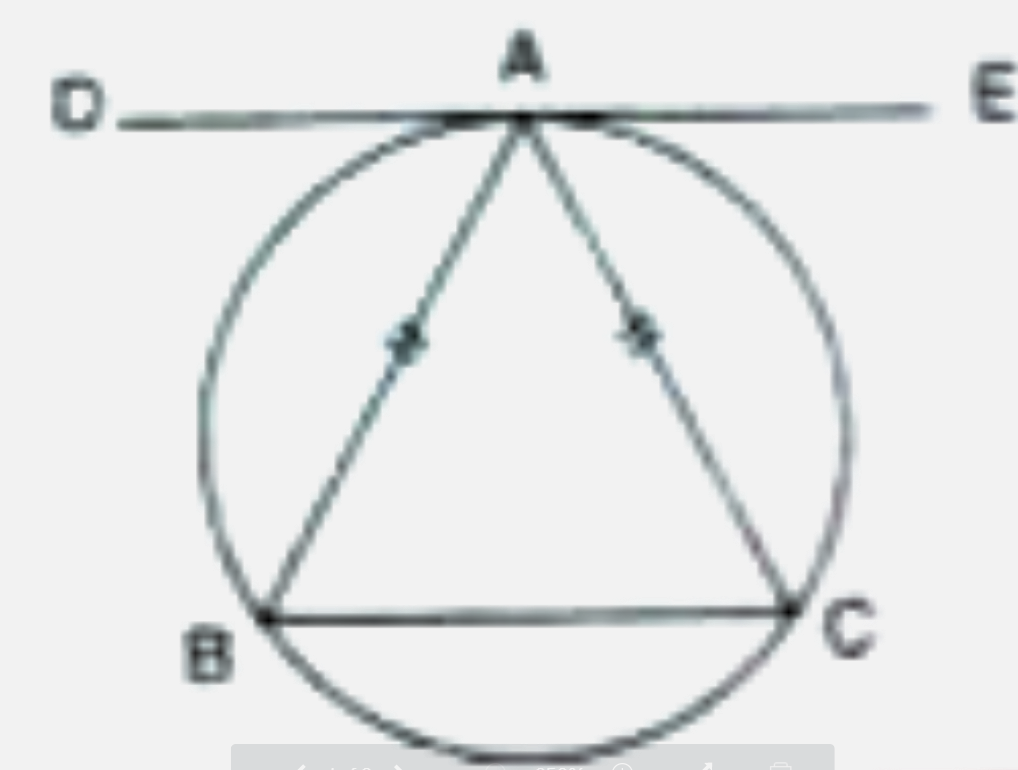
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
View SolutionAB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that `/_POQ=90^(@)`
View Solution
QUESTIONS questions and complete solutions for chapter TANGENTS AND INTERSECTING CHORDS of SELINA MATHS (ENGLISH) of Class 10