Complete Solutions to EXERCISE 18 (C) of chapter TANGENTS AND INTERSECTING CHORDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TANGENTS AND INTERSECTING CHORDS |
| SELINA PUBLICATION | EXERCISE 18 (C) |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Prove that , Of any two chords of a circle, show that the one which is nearer to the centre is larger.
View SolutionOABC is a rhombus whose three vertices. A, B and C lie on a circle with centre O.
(i) If the radiusof the circle is 10 cm, find the area of the rhombus.
(ii) If the area of the rhombus is `32sqrt(3)cm^(2)` find the radius of the circle.
View SolutionTwo circles with centres A and B and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q, find the length of PQ.
View SolutionTwo chords `A B` and `A C` of a circle are equal. Prove that the centre of the circle lies on the angle bisector of `/_B A Cdot`
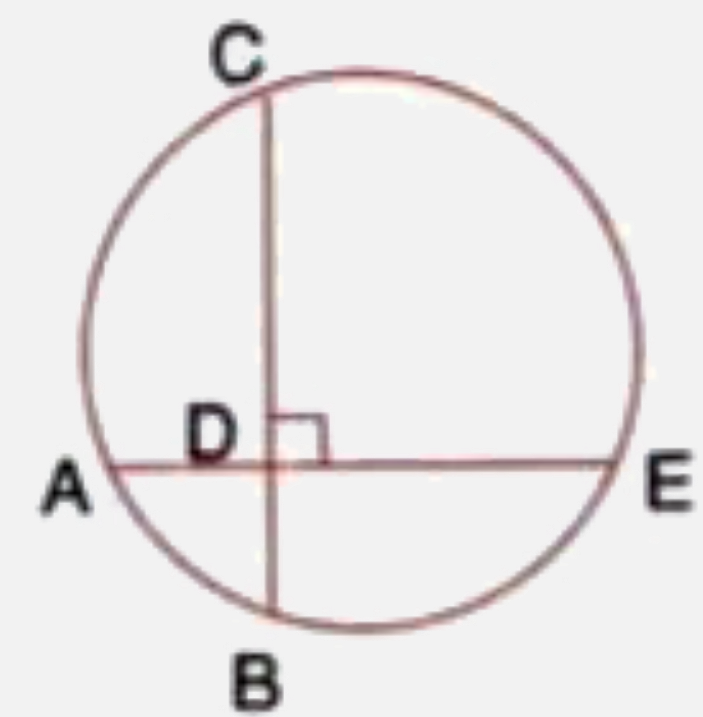
View SolutionThe diameter and a chord of a circle have a common end point. If the lengt of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chrod from the centre of the circle?
View SolutionABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle `ADC=110^(@)` and angle `BAC=50^(@)`. Find angle DAC and angle DCA.
View SolutionIn the given figure, C and D are points on the semi circle described on AB as diameter. Given angle `BAD=70^(@)` and angle `DBC=30^(@)`, calculate angle BDC

View SolutionIn cyclic quadrilateral `ABCD,/_A=3/_C` and `/_D=5 /_B`. Find the measure of each angle of the quadrilateral.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionBisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D,E and F respectively. Prove that angle `EDF=90^(@)-1/2/_A`
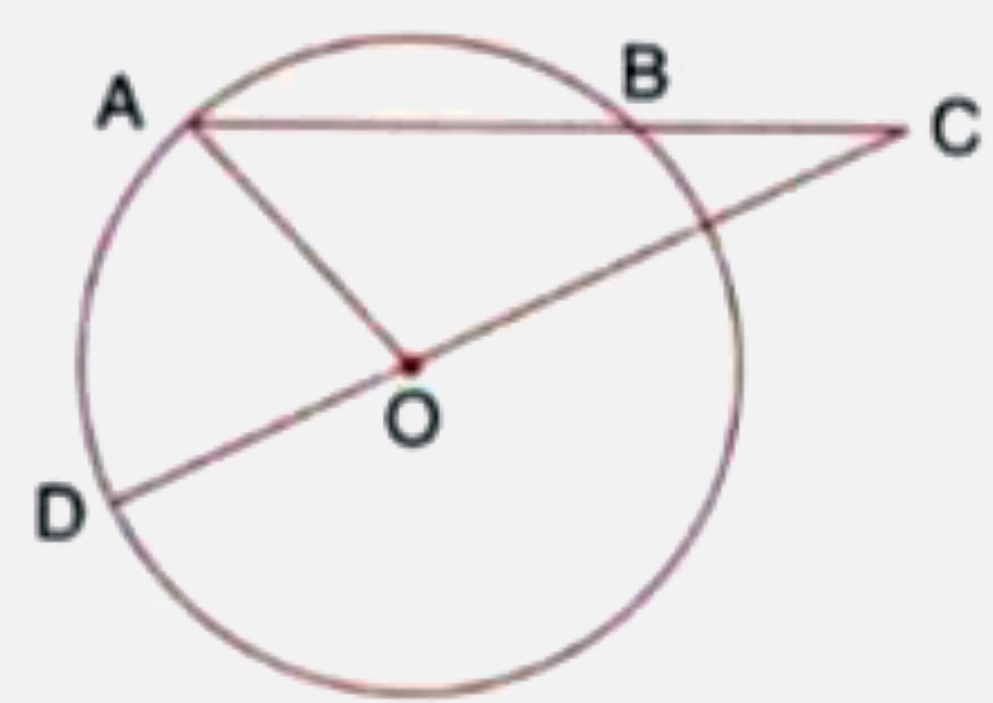
View SolutionIn the figure AB is the chord of a circle with centre O and DOC is a line segment such that `BC=DO`. If `/_C=20^(@)`, find angle AOD.
View SolutionProve that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
View Solution. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View SolutionIn the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
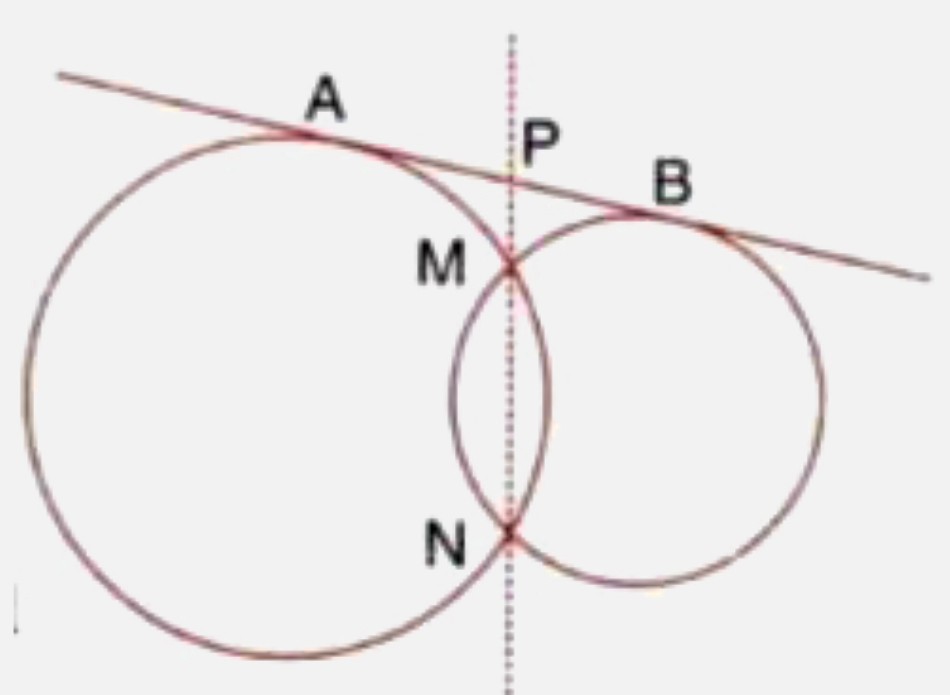
Prove that the line NM produced bisects AB at P.
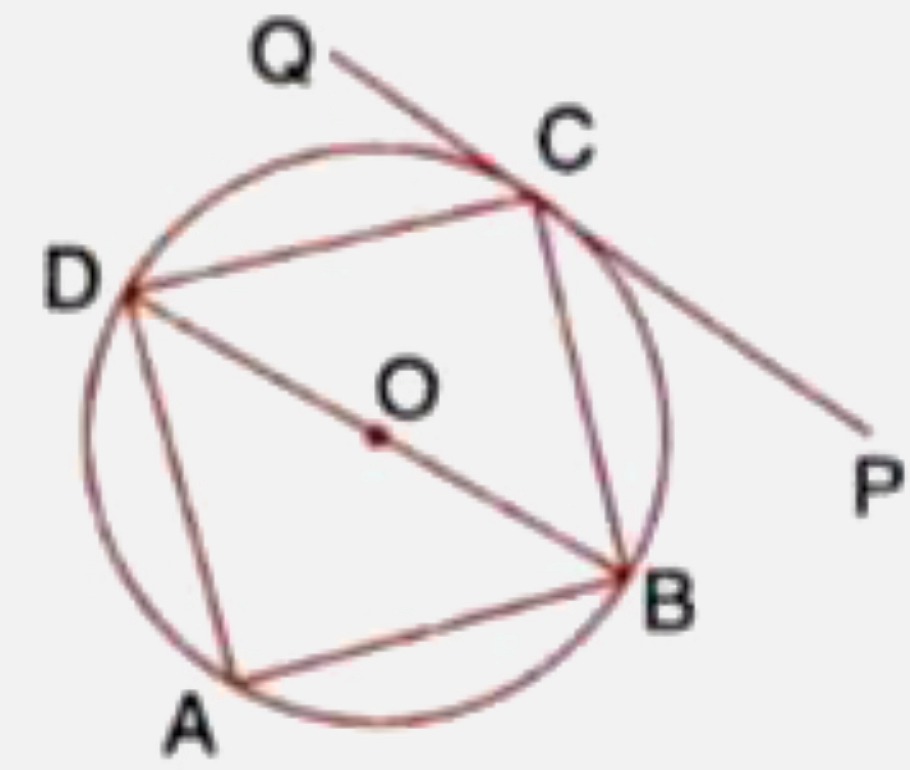
View SolutionIn the given figure, ABCD is a cyclicquadrilateral, PQ is tangent to the circle at point C and BD is its diameter.
If `/_DCQ=40^(@)` and `/_ABD=60^(@)` find
(i) `/_DBC`
(ii) `/_BCP`
(iii) `/_ADB`
View SolutionThe given figure shows a circle with centre O and BCD is tangent to it at C. Show that
`/_ACD+/_BAC=90^(@)`

View SolutionABC is a right triagle with angle `B=90^(@)` . A circle with BC as diameter meets hypotenuse AC and point D. Prove that
(i) `ACxxAD=AB^(2)`
(ii) `BD^(2)=ADxxDC`
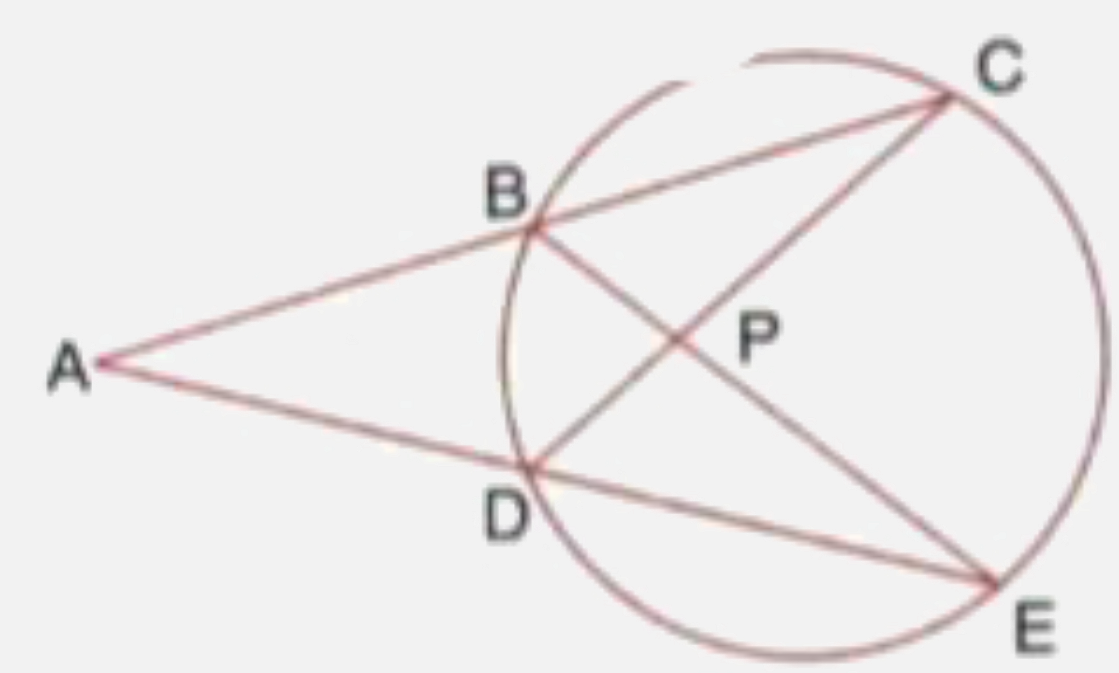
View SolutionIn the given figure `AC=AE`
Show that
(i) CP=EP
(ii) BP=DP
View SolutionABCDE is a cyclic pentagon with centre of its circumcircle alt point O such that AB=BC=CD and angle `ABC=120^(@)`
Calculate
(i) `/_BEC` (ii) `/_BED`
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meet at C. If `/_ACO=30^(@)` find
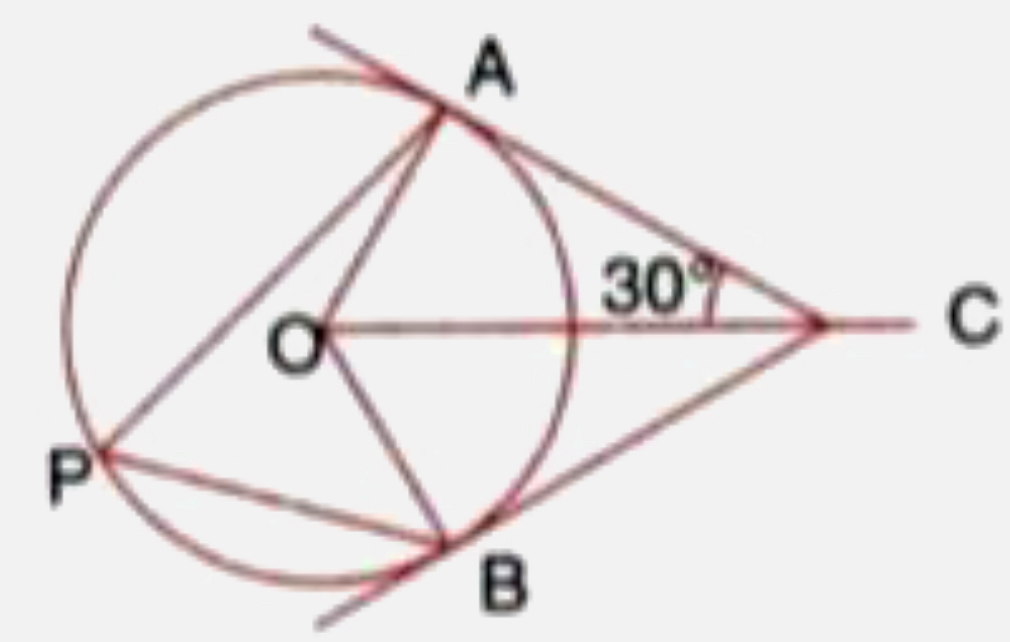
(i) `/_BCO`
(ii) `/_AOB`
(iii) `/_APB`
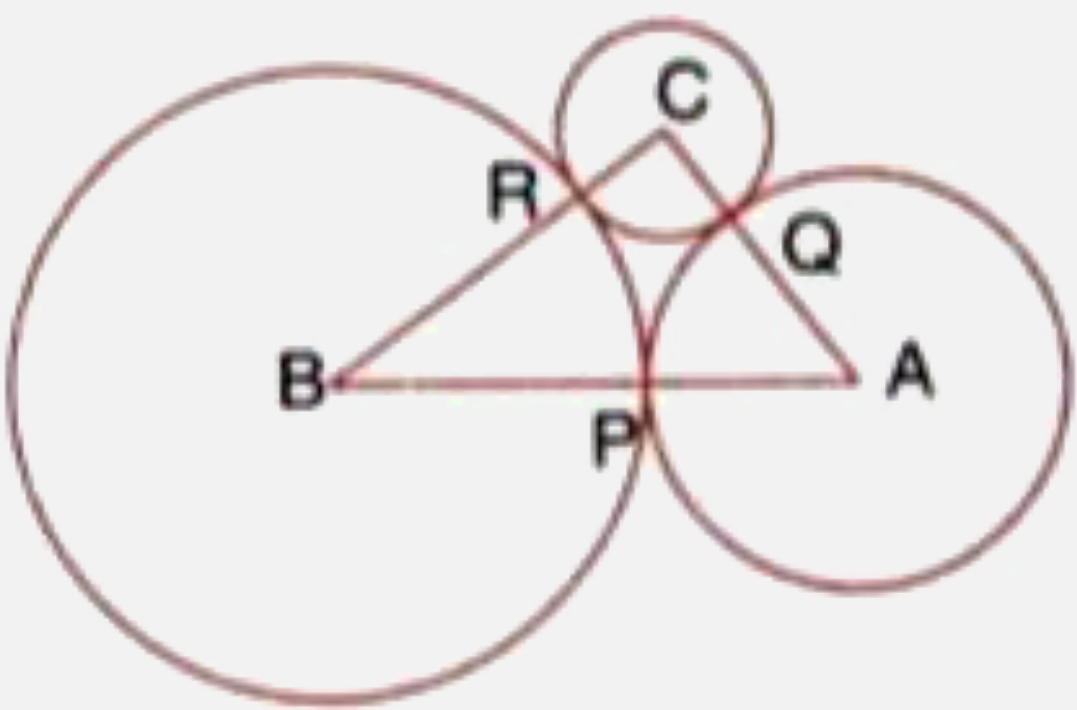
View SolutionABC is a triangle with AB=10cm, BC=8cm and AC=6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres Find the radii of the three circles.
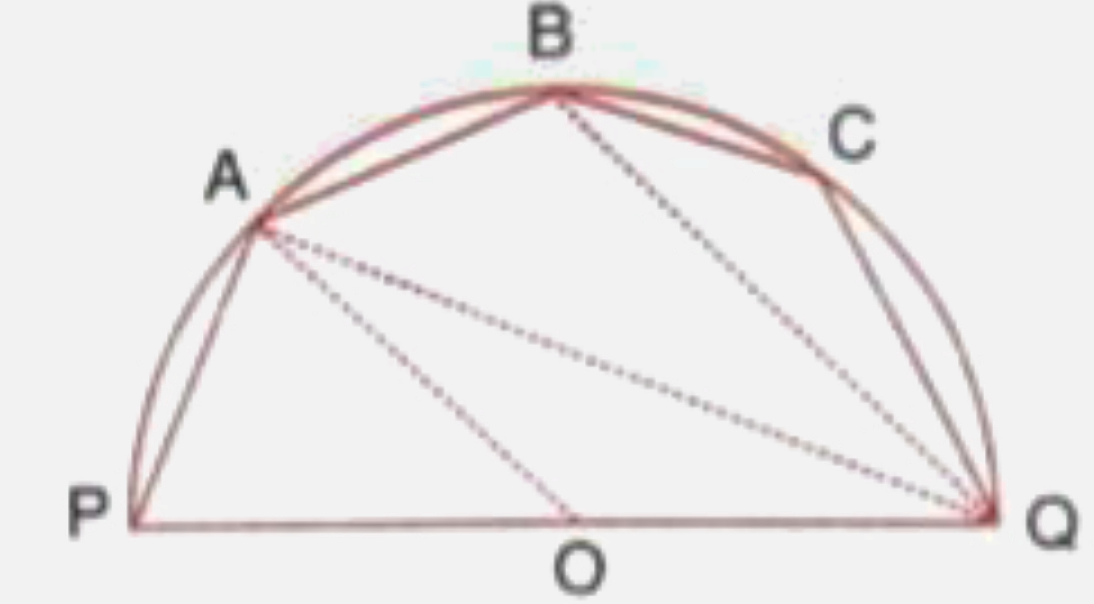
View SolutionThe given figure shows a semi circle with centre O ane diameter PQ. If PA=AB and `/_BCQ=140^(@)` find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
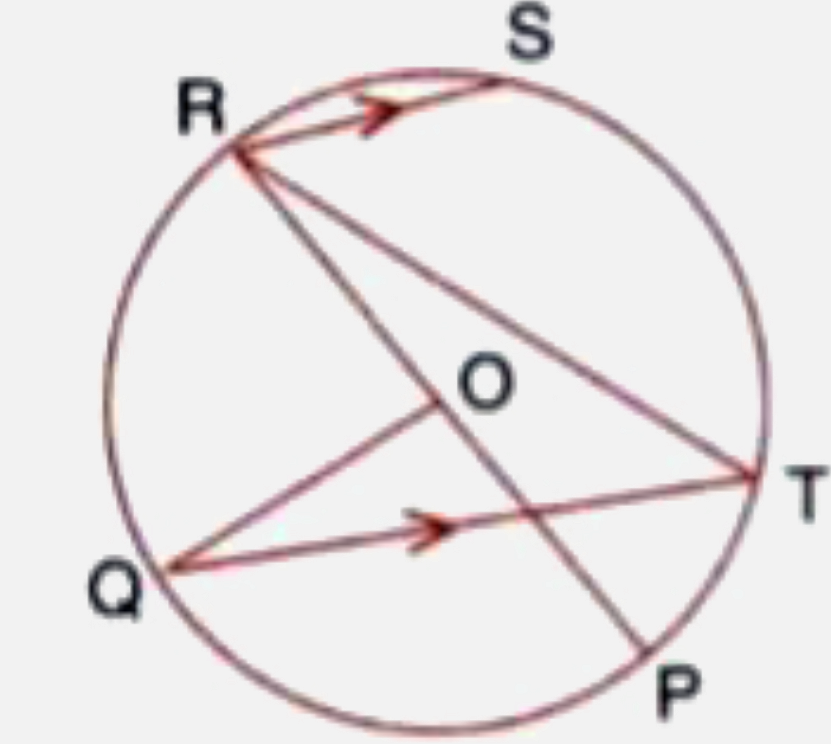
View SolutionThe given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle `PRT=20^(@)` and angle `POQ=100^(@)` calculate
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR
View SolutionIn the given figure PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that
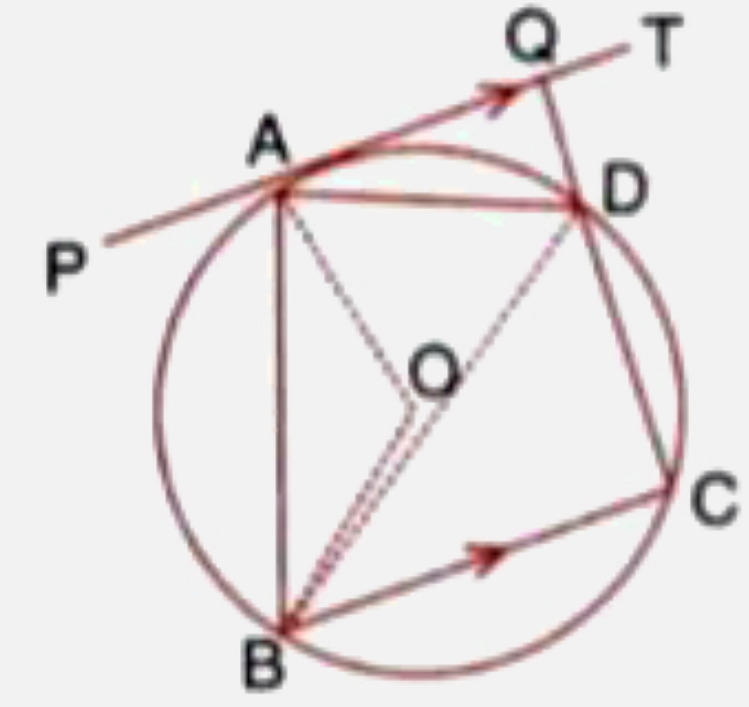
(i) `/_BAP=/_ADQ`
(ii) `/_AOB=2/_ADQ`
(iii) `/_ADQ=/_ADB`
View SolutionAB is a line segment and M is its mid point. Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all thethree semi- circles. Show that `AB=6xxr`
View SolutionTA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionProve that the any four vertices of a regular pentagon are concyclic (lie on the same circle).
View SolutionChords AB and CD of a circle when extended meet at point X. Given AB =4 cm, BX=6 cm and XD=6cm, calculate the length of CD.
View SolutionIn the given figure find TP if AT=16 cm and AB=12 cm.
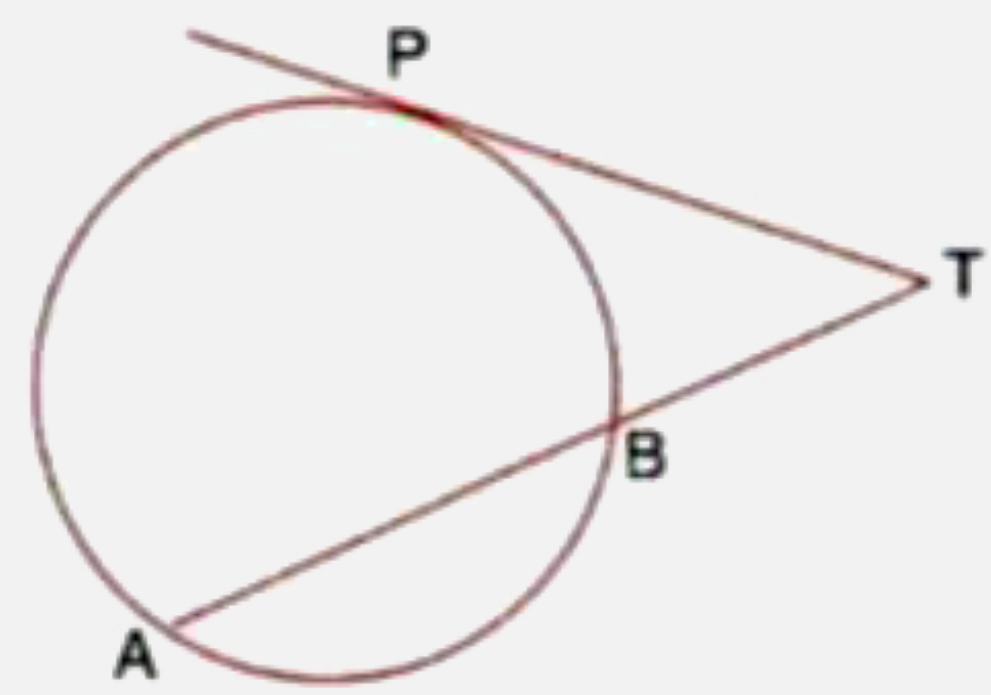
View SolutionIn the following figure, a circle is inscribed in th equadrilaterial ABCD.
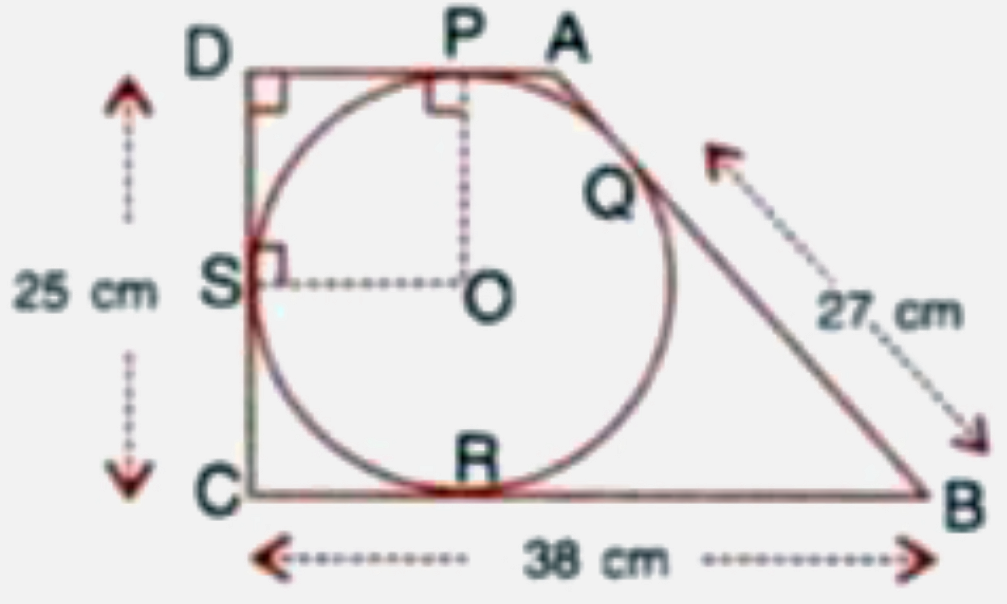 width="80%">
width="80%">
If BC=38 cm, QB=27cm, DC=25 cm and that AD is perpendicular to DC, find the radius of the circle.
View SolutionIn the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
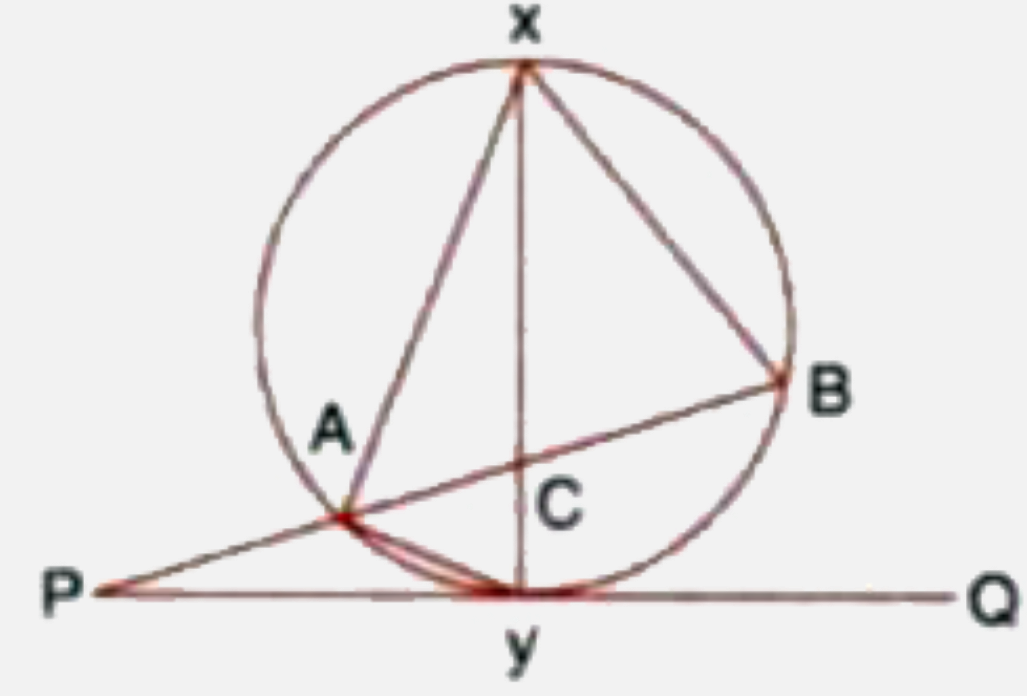
If `/_AXB=50^(@)` and `/_ABX=70^(@)` find `/_BAY` and `/_APY`
View SolutionIn the given figure QAP is the tangent at point A and PBD is a straight line.
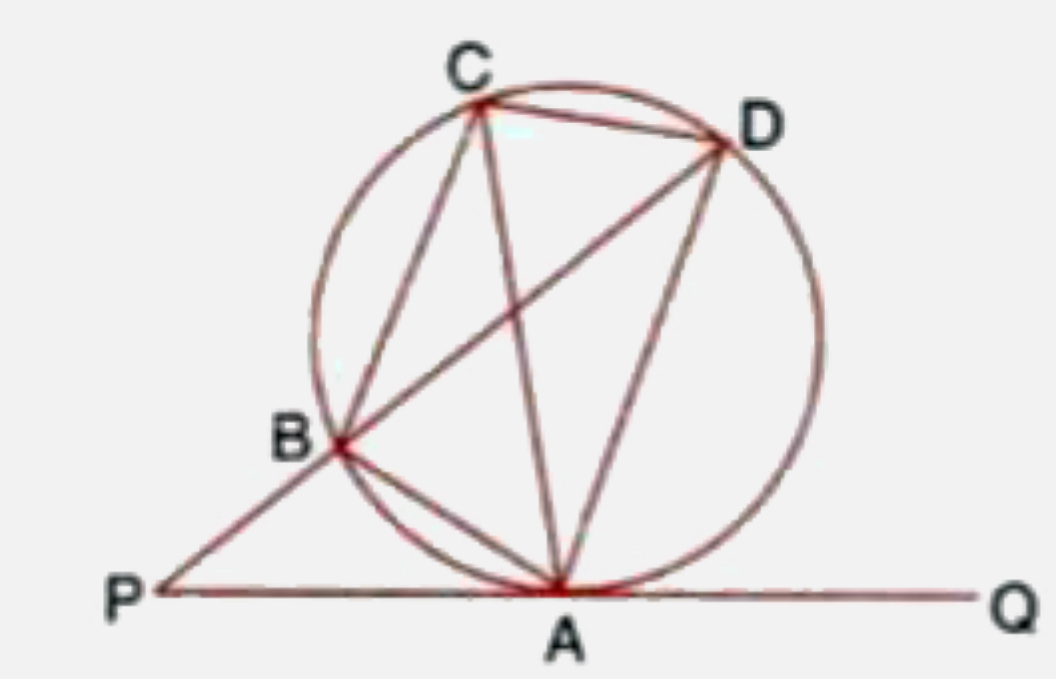
If `/_ACB=36^(@)` and `/_APB=42^(@)`, find
(i) `/_BAP` (ii) `/_ABD`
(iii) `/_QAD` (iv) `/_BCD`
View SolutionIn the given figure AB is the diameter. The tangent at C meets AB produced at Q.

If `/_CAB=34^(@)` find
(i) `/_CBA` (ii)`/_CQB`
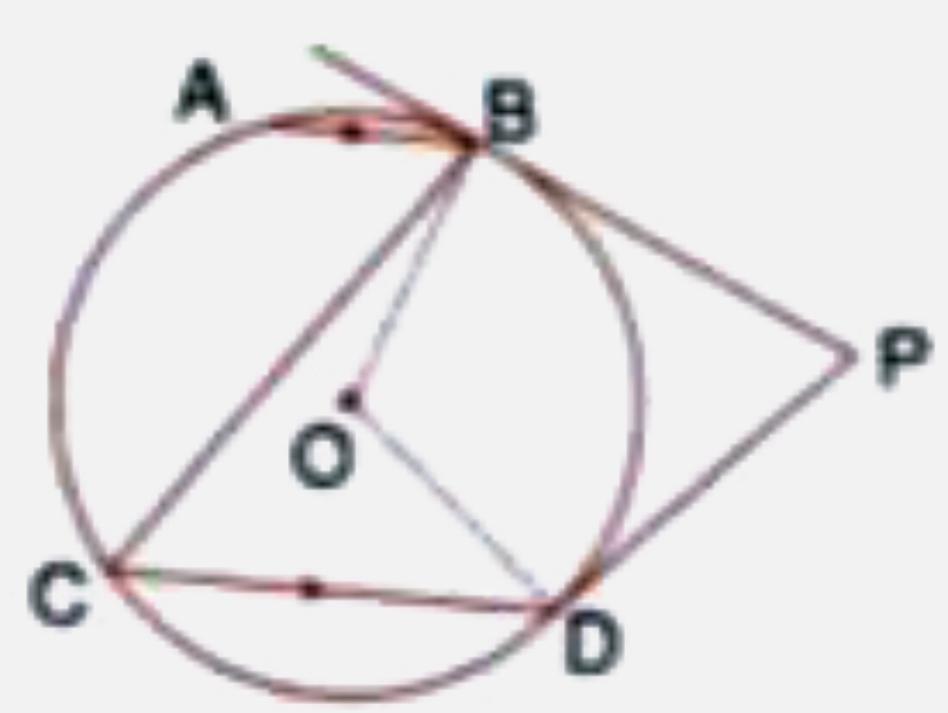
View SolutionIn the given figure O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and `/_ABC=55^(@)`, find :
(i) `/_BOD` (ii) `/_BPD`
View SolutionIn the following figure PQ=QR`, /_RQP=68^(@)`, PC and CQ are tangents to the circle with centre O.

Calculate the values of (i) `/_QOP` (ii) `/_QCP`
View Solutionabout to only mathematics
View SolutionIn the figure given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
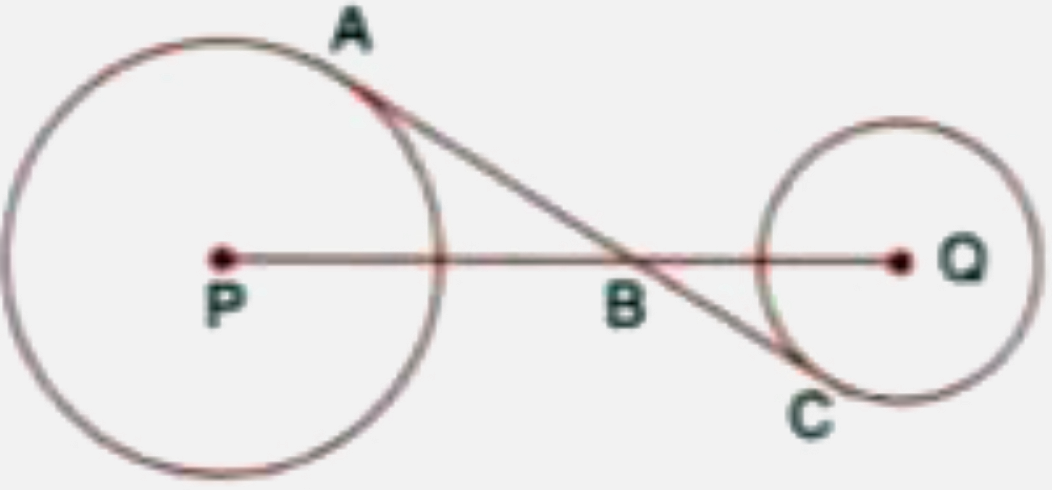
Given that AB=8 cm calculate PQ.
View SolutionIn the figure given below O is the centre of the circumcircle of triangle XYZ.
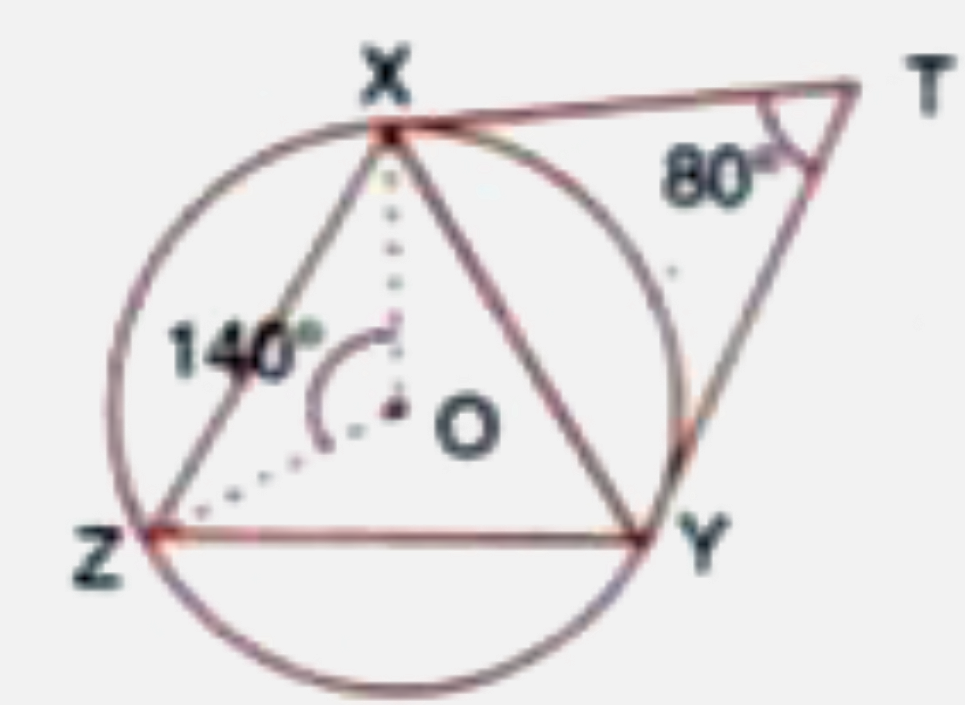
Tangents at X and Y intersect at point T. Given `/_XTY=80^(@)` and `/_XOZ=140^(@)`, calculate the value of `/_ZXY`.
View SolutionIn the given figure, AE and BC intersect each other at point D.
If `/_CDE=90^(@),AB=5cm,BD=4` and `CD=9` find AE
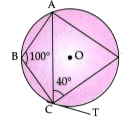
View SolutionIn the given circle with centre O, `angleABC=100^(@),angleACD=40^(@)` and CT is a tangent to the circle at C. Find the `angleADCandangleDCT`.
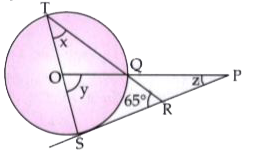
View SolutionIn the figure given below, O is the centre of the cirlce and SP is a tangent. If `angleSRT=65^(@)`, find the value of x, y and z.
View Solution
EXERCISE 18 (C) questions and complete solutions for chapter TANGENTS AND INTERSECTING CHORDS of SELINA MATHS (ENGLISH) of Class 10