Complete Solutions to EXAMPLE of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| CP SINGH | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A partical moves `5M` towards east and then `12m` towards north. Find the displacement and distance covered.
View SolutionA particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
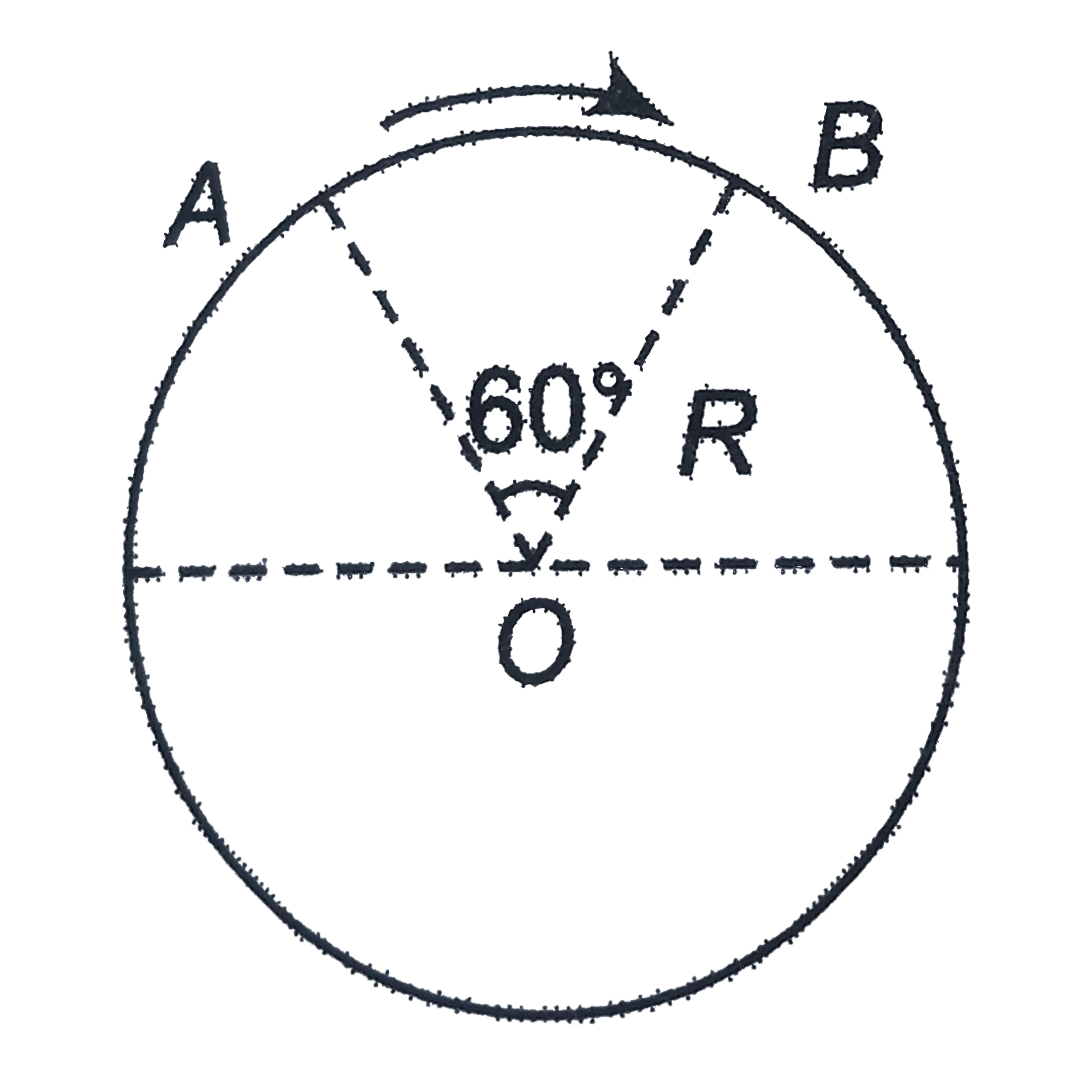
View SolutionA particle moves in a of radius R from `A` to `B`, as shown in the figure. Find the distance and displacement covered.
View SolutionA partical moves in a straifgt line from `A` to `B` for the first `30 km` with speed `10 km//h` and the next `60 km` with speed `20 km//h`. Find the average speed and average velocity.
View SolutionA particle moves in a straight line from `A` to `B`
(a) for the first half of distance with speed `v_(1)` and the next half of distance with speed `v_(2)`.
(b) for the first one-third distance with speed `v_(1)` and the next two-third distance with speed `v_(2)`.
(c ) for the first one-fourth distance with speed `v_(0)`, the next half of distance with speed `2v_(0)` and the last one-fourth distance with speed `3v_(0)`.
Find the average speed in each case.
View SolutionA particle moves in a straight line from `A` to `B` with speed `v_(1)` and then from `B` to `A` with speed `v_(2)`. Find the average velocity and average speed.
View SolutionA partical moves from `A` to `B` for the first one-third with speed `v_(1)` and the next two-third time with speed `v_(2)`. Find the average speed.
View SolutionA point traversed half the distance with a velocity `v_0`. The remaining part of the distance was covered with velocity `v_1` for half the time, and with velocity `v_2` for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
View SolutionA partical is moving in a straight line under constant acceletation. If the motion starts from rest, Find the ratio of displacement in `n` second to that in the `n^(th)` second.
View SolutionA particle is moving in a straight line under constant acceleration. It travels `15 m` in the `3^(rd)` second and `31 m` in the `7^(th)` second. Find the initial velocity and constant acceleration.
View SolutionIn the pervious problem, find the displacement in `10 s` and `10^(th)` second.
View SolutionA particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval `t_(0)`.
View SolutionA particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement `d`.
View Solutiontwo particles `A` and `B` are at separation of `100 m`. They move towards each other with uniform speed, `A` with `5 m//s` and `B` with `15 m//s`. When and where the two particle meet?
View SolutionIf in the previous problem, particle `A` moves with constant acceleration `4 m//s^(2)` with initial speed `5 m//s` and `B` moves with uniform speed `12 m//s`, when and where the particle meet?
View SolutionA bus starts from rest and moves with constant acceleration `8 m//s^(2)`. At the same time, a car traveling with a constant velocity `16 m//s` overtakes and passes the bus. After how much time and at what distance the bus overtakes the car?
View SolutionA boy is moving with constant velocity `12 m//s`. When he is `32 m` behind a cyclist, the cyclist starts from rest and moves under constant acceleration `2 m//s^(2)`. After how much time the boy meets the cyclist? Explain reason for two answers.
View SolutionA boy is moving with constant velocity `v_(0)`on a straight road. When he is at a distance `d` behind the bus, the bus starts from rest and moves with a constant acceleration `alpha`. Find the minimum value of `v_(0)` so that the boy catches the bus.
View SolutionCar `A` starts from a point `O` and moves with constant velocity `9 m//s`. After `2 s`, another car `B` begins its journey from `O` and follows car `A`. If car `B` starts from rest and moves under constant acceleration `4 m//s^(2)`, after how much time and at what distance from `O` the cars meet?
View Solution(a) If a train traveling at `72 km//h` is to be brought to rest in a distance of `200 m`, find the deceleration.
(b) The velocity of a bullet is reduced from `200 m//s` to `100 m//s` while traveling through a wooden block of thickness `10 cm`. Find the retardation (assuming it ti be uniform).
View SolutionA car is moving with constant speed `15 m//s`. Suddenly the driver sees an obstruction on the road and takes `0.40 s` to apply the brake, the brake causes a deceleration of `5 m//s^(2)`. Find the distance traveled by the car before it stops.
View SolutionA car is moving with speed `20 m//s`. Suddenly the driver sees the sign of danger at a distance of `50 m`, after a certain reaction time `t_(0)`, he applies breaks to cause deceleration `5 m//s^(2)`. What is the maximum allowable reaction time `t_(0)` to avoid accident and distance traveled by the car during reaction time?
View Solution(a) A particle moving with constant acceleration from `A` to `B` in a straight line `AB` has velocities `u` and `v` at `A` and `B` respectively. Find the velocity of the particle at the midpoint of `AB`.
(b) If the time taken by the particle to go from `A` to the midpoint of `AB` is two times that from the midpoint of `AB` to `B` then find the value of `v//u`.
View SolutionA car accelerates from rest at a constant rate ` alpha ` for some time after which it decelerates at a constant rate ` beta` to come to rest. If the total time lapse is ` t` seconds , evauate.
(i) maximum velocity reached , and
(ii) the total distance travelled .
View SolutionA particle starts from rest and moves with a constant acceleration of `4 m//s^(2)` for `10 s`, then it moves under constant seceleration and stops in `20 s`. Find (a) the maximum velocity attained by the particle (b) the total distance traveled and (c ) the distance/distances from the origin, when the particle is moving at half the maximum velocity.
View SolutionA train starts from station `A` with uniform acceleration `a_(1)`. For some distance and then goes with uniform retardation `a_(2)` for some more distance to come to rest at station `B`. The distance between stations `A` and `B` is `4 km` and the train takes `1//5 h` to compete this journey. If accelerations are in km per minute unit, then show that `(1)/(a_(1)) +(1)/(a_(2)) =x`. Find the value of `x`.
View SolutionBetween two points, a car accelerates uniformly at first, then moves with constant speed and finally retards uniformly to rest. If the ratio of time takes is `1:4:2` and the maximum speed is `70 km//h`, find the average speed over the whole journey.
View SolutionA partical starts from rest and moves in a straight line. It travels a distance L with uniform acceleration and then moves with constant velocity a further distance `2L`. Finally, it comes to rest after moving a further distance 4L under uniform retardation. Find the ratio of average speed to the maximum speed.
View SolutionA car starts moving rectilinearly first with acceleration `alpha=5 m s^(-2)` (the initial velocity is equal to zero), then uniformly, and finally, deceleration at the same rate `alpha` comes to a stop. The time of motion equals `t=25 s`. The average velocity during this time is equal to `
72 kmh^(-1)` How long does the car move uniformly?
View SolutionThe speed of a train increases at a constant rate `alpha` from zero to v and then remains constant for an interval and finally decreases to zero at a constant rate `beta`. The total distance travelled by the train is l. The time taken to complete the journey is t. Then,
View SolutionTwo trains, each having a speed of `30 km//h`, are headed towards each other
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration `a_1 and a_2` respectively. Show that `v=sqrt (a_1 a_2) t.`
View SolutionA particle is dropped from the top of a tower of height `80 m`. Find the time of jurney and the speed with which it strikes the ground.
View SolutionA particle is dropped the top of a tower. Its displacement in the first three seconds and in the last second is the same. Find the height of the tower.
View SolutionA particle is dropped from the top of a tower. If it falls half of the height of the tower in its last second of journey, find the time of journey.
View SolutionIf in the previous problem, the particle travels `9//25` of the distance in its last second, find the time of fall and the height of the tower.
View SolutionA particle is dropped from the top of a tower.
(a) Find the ratio of displacement in successive time interval `t_(0)`.
(b) Find the ratio of time in falling successive distances `h`.
View SolutionDrops of water fall at regular intervals from the roof of a building of height `h=16m`. The first drop striking the ground at the same moment as the fifth drop is ready to leave from the roof. Find the distance between the successive drops.
View SolutionA ball is dropped from a height. If it takes `1 s` to cross the last `55 m` before hitting the ground, find the height from which it was dropped.
View SolutionA particle is dropped from some height. After falling through height h, the velocity of the particle becomes `v_(0)`. If it further falls through a distance `y(y lt lt h)`, find the approximate increase in velocity in terms of `v_(0),y` and `h`.
View SolutionA body is dropped from a large height h in time `t_(0)` second. Find the time taken to cover the last meter of fall in terms of `t_(0)`
View SolutionTwo particles begin to fall freely from the same height but the second falls `t_(0)` second after the first. Find the time (after the dropping of first) when separation between the particles is `h_(0)`.
View SolutionA ball is dropped from the top of a tower. After `2 s` another ball is thrown vertically downwards with a speed of `40 m//s`. After how much time and at what distance below the top of tower the balls meet?
View SolutionA ball is dropped from the top of an 80 m high tower After 2 s another ball is thrown downwards from the tower. Both the balls reach the ground simultaneously. The initial speed of the second ball is
View SolutionA particle is thrown vertically upward with speed `40 m//s`.
(a) After how much time attains maximum height?
(b) Find (i) the maximum height attained by the particle.
(ii) the velocity at half of the maximum height.
(c ) Find (i) the ratio of distances in the first half and the next half of time.
the ratio of the time in the first half and the second half of the distance (consider only upward journey)
View SolutionA ball is thrown vertically up with a velocity `u`. It passes three points `A, B` and `C` in its upward journey with velocities `u/s,u/3` and `u/4`, respectively. Find `(AB)/(BC)`.
View SolutionIf a ball is thrown vertically upwards with speed `u`, the distance covered during the last `t` second of its ascent is
View SolutionA ball is thrown vertically upward with speed `40 m//s`. Simultaneously, another ball is dropped from a height `200 m` in the same verticle line. When and where the balls meet?
View SolutionA ball is thrown vartically upward with speed `70 m//s`. After 1 s, another ball is dropped from a height `185 m` in the same vertical line. When and where the balls collide?
View SolutionFrom the foot of a tower `80 m` high, a stone is thrown up so as to reach the top of a tower. After `2 s`, another stone is dropped from the top of the tower. When and where the two stones meet?
View SolutionA ball is thrown vertically upward with velocity `20 m//s` from a tower of height 60 m. After how much time and with what velocity will it strike the ground?
View SolutionIn the previous problem, find the magnitude and direction of velocity after `1 s, 3 s` and `5 s`. Also find the distance of the ball from the ground at these instances.
View SolutionA balloon carring a stone is moving vartically upward with velocity `12 m//s`. When the balloon is at height `64 m`, the stone is dropped. After how much time and with what velocity will it strike the ground?
View SolutionTwo balls are projected simultaneously with the same speed from the top of a tower, one vertically upwards and the other vertically downwards. They reach the ground in 9 s and 4 s, respectively. The height of the tower is `(g=10 m//s^(2))`
View SolutionA body is thrown vertically upwards from `A`. The top of a tower . It reaches the ground in time `t_(1)`. It it is thrown vertically downwards from `A` with the same speed it reaches the ground in time `t_(2)`, If it is allowed to fall freely from `A`. then the time it takes to reach the ground.
 .
.
View SolutionA body is vertically upwards. If `t_(1)` and `t_(2)` are the times at which it is height h above the point of projection while ascending and descending, respectively, find (a) the velocity of projection and height h, (b) the maximum height reached by the body and (c ) the velocity of the body at height `h//2`.
View SolutionA particle is projected vertically upwards from a point O on the ground. It takes time `t_(1)` to reach a point `A` at a height h above the ground, it continues to move and takes a time `t_(2)` to reach the ground. Find (a) h, (b) the maximum height reached and (c ) the velocity of the partical at the half of maximum height.
View Solutiontwo particals are thrown vertically upward with the same initial velocity of `50 m//s` but `2 s` apart. How long after the first one thrown, will they meet?
View SolutionA particle is thrown vertically upward with speed `45 m//s`. Find the distance covered by the particle in the `5^(th)` second of its journey.
View SolutionA parachutist after bailing out falls `80 m` without friction. When the parachute opens, he decelerates downward with `5m//s^(2)` and reaches the ground with a speed of `10 m//s`. (a) How long is the parachutist in air? (b) At what height did bail out?
View SolutionA rocket is fired vertically upward from the ground with a resultant vertical acceration of `5 m//s^(2)`. The fuel is finished in `100 s` and it continues to move up. After how much time from then will the maximum height be reached and what is the maximum height?
View SolutionA balloon rises from rest on the ground with constant acceleration `g`//`8.` A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA roket fired vertically ascends with a constant acceleration `g//3` for `1 min`. Its fuel is then all used and it continues to rise as a free body. What is the maximum height reached? What is the total time elapsed from the take off until the rocket strikes the earth?
View SolutionA partical is moving in a straight line such that its displacement at any time t is given by `s=4t^(3)+3t^(2)`. Find the velocity and acceleration in terms of t.
View SolutionA partical moves along a straight line such that its displacement `s=alphat^(3)+betat^(2)+gamma`, where t is time and `alpha`, `beta` and `gamma` are constant. Find the initial velocity and the velocity at `t=2`.
View SolutionA partical is moving in a straight line such that ita velocity is given by `v=t^(4)+3t^(2)+8 m//s`. Find acceleration at time `t=1 s`.
View SolutionThe displacement of a partical as a function of time t is given by `s=alpha+betat+gammat^(2)+deltat^(4)`, where `alpha`,`beta`,`gamma` and `delta` are constants. Find the ratio of the initial velocity to the initial acceleration.
View SolutionA partical is moving in a straight line such that `s=t^(3)-3t^(2)+2`, where `s` is the displacement in meters and `t` is in seconds. Find the
(a) velocity at `t=2s`, (b) acceleration at `t=3s`,
( c) velocity when acceleration is zero and
(d) acceleration when velocity is zero.
View SolutionThe displacement of a particla moving in straight line is given by `s=t^(4)+2t^(3)+3t^(2)+4`, where s is in meters and t is in seconds. Find the
(a) velocity at `t=1 s`, (b) acceleration at `t=2 s`,
(c ) average velocity during time interval `t=0` to `t=2 s` and
(d) average acceleration during time interval `t=0` to `t=1 s`.
View SolutionThe displacement x of a particle moving in one dimension under the action of a constant force is related to time t by the equation `t=sqrt(x)+3`, where x is in meter and t is in second. Find the displacement of the particle when its velocity is zero.
View SolutionA particle is moving such that the velocity is given by `v=sqrt(2gammas)`, where `gamma` is constant and s is diplacement. Find the acceleration.
View SolutionA particle moves in a straight line as `s =alpha(t-4)+beta(t-4)^(2)`. Find the initial velocity and acceleration.
View SolutionThe displacement of a particle varies as `s=k/alpha(1-e^(-alphat))`, where `k` and `alpha` are constants. Find the velocity and acceleration in terms of t and their initial values.
View SolutionA partical moves in a straight line as `s=alpha(t-2)^(3)+beta(2t-3)^(4)`, where `alpha` and `beta` are constants. Find velocity and acceleration as a function of time.
View SolutionIf the time and displacement of the particle along the positive x-axis are related as `t=(x^(2)-1)^(1//2)`, find the acceleration in terms of `x`.
View SolutionThe relation between time t and displacement x is `t = alpha x^2 + beta x,` where `alpha and beta` are constants. The retardation is
View SolutionThe position of particle moving along the x-axis veries with time t as `x=6t-t^(2)+4`. Find the time-interval during which the particle is moving along the positive x-direction.
View SolutionA particle is moving such that `s=t^(3)-6t^(2)+18t+9`, where s is in meters and t is in meters and t is in seconds. Find the minimum velocity attained by the particle.
View SolutionA particle is moving with velocity `v=t^(3)-6t^(2)+4`, where v is in `m//s` and t is in seconds. At what time will the velocity be maximum//minimum and what is it equal to?
View SolutionA particle is moving along the x-axis such that `s=6t-t^(2)`, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval `t=0` to `t=5 s`.
View SolutionA particle moves along the x-axis according to `s=t^(3)-15/2t^(2)+12t+5`, where the symbols have their usual meaning.
(a) Determine the time when speed is increasing//decreasing.
(b) At what time, the velocity changes its direction?
(c ) Find the distance traveled in the first six seconds.
View SolutionRefer to Example 30, if the time of journey is minimum, find the value of v in terms of given quantities and also the minimum time.
View SolutionA particle is moving under constant acceleration `a=k t`. The motion starts from rest. The velocity and displacement as a function of time t is
View Solutionif `a=3t^(2)+2t`, initial velocity is `5 m//s`. Find the velocity at t=4s. The motion is in straight line, a is acceleration in `m//s^(2)` and t is time in seconds.
View SolutionA particle in moving in a straight line such that its velocity is given by `v=12t-3t^(2)`, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at `t=3 s`.
View SolutionA particle is moving under constant acceleration `a=alphat+betat^(2)`, where alpha beta constants. If the position and velocity of the partical at start, i.e. `t=0` are `x_(0)` and `v_(0)`, find the displacement and velocity as a function of time t.
View SolutionThe deceleration exerienced by a moving motor blat, after its engine is cut-off is given by `dv//dt=-kv^(3)`, where `k` is constant. If `v_(0)` is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time `t` after the cut-off is.
View SolutionA particle moves with an initial velocity `v_(0)` and retardation alphav, where alpha is a constant and v is the velocity at any time t. If the particle is at the origin at `t=0`, find
(a) (i) velocity as a function of time t.
(ii) After how much time the particle stops?
(iii) After how much time velocity decreases by `50%`?
(b) (i) Velocity as a function of displacement s.
(ii) The maximum distance covered by the particle.
(c ) Displacement as a function of time t.
View SolutionThe motion of a body is given by the equation `dv//dt=6-3v`, where v is in m//s. If the body was at rest at `t=0`
(i) the terminal speed is `2 m//s`
(ii) the magnitude of the initial acceleration is `6 m//s^(2)`
(iii) The speed varies with time as `v=2(1-e^(-3t)) m//s`
(iv) The speed is `1 m//s`, when the acceleration is half initial value
View SolutionA particle is moving in sand under acceleration `a=g-lambday^(2)`, where lambda is a positive constant and `y` is the distance traveled on the y-axis. If the initial velocity is `v_(0)` and after traveling a distance `y_(m)`, the particle stops, find `lambda` (the motion is along the y-axis).
View SolutionThe velocity of a particle moving in the `x` direction varies as `V = alpha sqrt(x)` where `alpha` is a constant. Assuming that at the moment `t = 0` the particle was located at the point `x = 0`. Find the acceleration.
View SolutionA point moves linearly with deceleration which is given by `dv//dt=-alphasqrt(v)`, where alpha is a positive constant. At the start `v=v_(0)`. The distance traveled by particle before it stops will be
View SolutionThe velocity of a particle moving along the xaxis is given by `v=v_(0)+lambdax`, where `v_(0)` and lambda are constant. Find the velocity in terms of t.
View Solution(a) At the moment `t=0`, a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity is given by `v=10-2t`. Find the displacement and distance in the first `8s`.
(b) If `v=t-t^(2)`, find the displacement and distamce in first 2s.
View SolutionA particle is moving in a straight line such that its velocity varies as `v=v_(0) e^(-lambdat)`, where `lambda` is a constant. Find average velocity during the time interval in which the velocity decreases from `v_(0)` to `v_(0)/2`.
View SolutionThe velocity of a particle is given by `v=v_(0) sin omegat`, where `v_(0)` is constant and `omega=2pi//T`. Find the average velocity in time interval `t=0 `to `t=T//2.`
View SolutionThe displacement-time graph for two particles is as shown. Find the ratio of their velocities.
View SolutionFor a particle moving in a straight line, the position-time graph is as shown in the figure. Find the velocity of the particle at time `t=1 s` and `t=4 s`. Also sketch the v-t graph.
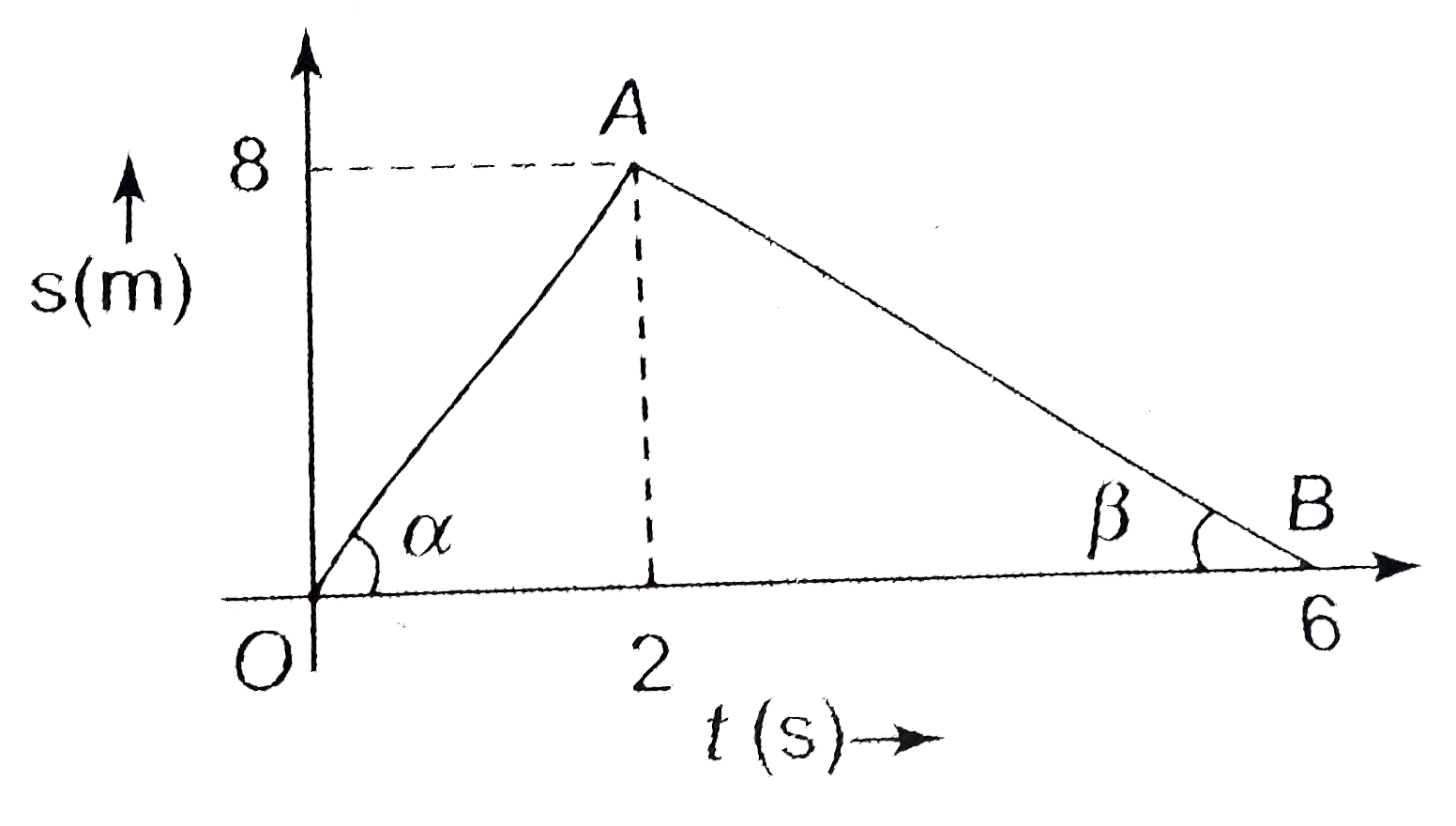
View SolutionThe displacement-time graph for a particle moving in a straight line is as shown in the figure. Determine the velocity of the particle at `t=1 s, 3 s` and `6 s`. Sketch the velocity-time graph.
View SolutionConsider the following st graph. What conclutions can be drawn regarding the velocity of the particle.
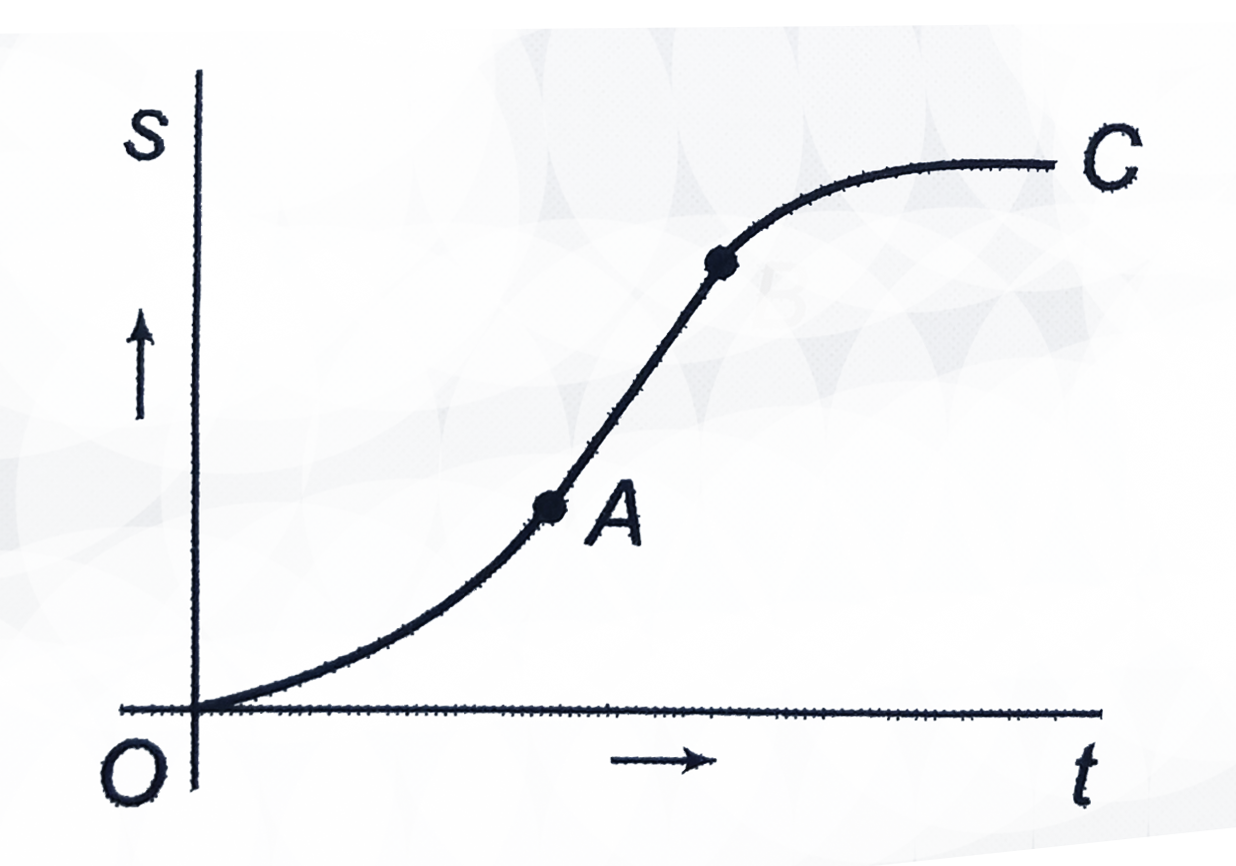
View Solution
EXAMPLE questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of CP SINGH PHYSICS (HINGLISH) of Class 11