Complete Solutions to Exercise of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| CP SINGH | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Three point masses, each of mass `m`, are placed at the corners of an equilateral triangle of side `L`. The moment of inertia of this system about an axis along one side of the triangle is
02:47View SolutionThe moment of inertia of a disc of mass `M` and radius `R` about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
01:01View SolutionLet `I_(A)` and `I_(B)` be moments of inertia of a body about two axes `A` and `B` respectively. The axis `A` passes through the centre of mass of the body but `B` does not. Then
01:35View SolutionA closed cylindrica tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tueb is rotated about a perpendicular bisector, the moment of inertia of water about the axis
02:36View SolutionA uniform cylinder has radius `R` and length `L`. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is `(mR^(2))/2` is equal to moment of inertia of the same cylinder about an axis passing through its centre and normal to its length, then
02:27View SolutionA solid sphere of mass `M`, radius `R` and having moment of inertia about as axis passing through the centre of mass as `I`, is recast into a disc of thickness `t`, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains `I`. Then, radius of the disc will be.
01:40View SolutionTwo circular discs are of same thickness. The diameter of `A` is twice that of `B`. The moment of inertia of `A` as compared to that of `B` is
02:12View SolutionThe moment of inertia of a circular disc of mass `M` and radius `R` about an axis passing thrugh the center of mass is `I_(0)`. The moment of inertia of another circular disc of same mass and thickness but half the density about the same axis is
03:22View SolutionFrom a uniform wire, two circular loops are made (`i`) `P` of radius `r` and (`ii`) `Q` of radius `nr`. If the moment of inertia of `Q` about an axis passing through its center and perpendicular to tis plane is `8` times that of `P` about a similar axis, the value of `n` is (diameter of the wire is very much smaller than `r` or `nr`)
03:13View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is `I_(1)`. The same rod is bent into a ring and its moment of inertia about a diameter is `I_(2)`. Then `I_(1)//I_(2)` is
02:06View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are `I_(A), I_(B), I_(O)` and `I_(C)` respectively.
04:17View SolutionThe `M.I.` of a rod about an axis through its center and perpendicular to it is `I_(0)`. The rod is bent in the middle so that the two halves make an angle `theta`. The moment of inertia of the bent rod about the same axis would be
02:47View SolutionThe moment of inertia of a thin uniform rod of mass `M` and length `L` about an axis passing through its mid-point and perpendicular to its length is`I_0`. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
01:05View SolutionThree rings, each of mass `m` and radius `r`, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
 02:49View Solution
02:49View SolutionTwo rings `A` (`2m,R`) and `B` (`m,R`) are placed such that these are perpendicular but common center. The `M.I.` of the system about an axis passing through the common center and perpendicular to the plane of `B` is
02:31View SolutionIf `I_(0)` is the moment of inertia body about an axis passing through its center of mass. The moment about a parallel axis and at distance `d` is `I=I_(0)+Md^(2)`. The variation of `I` with `d` is
01:41View SolutionA rod of length `L` is made of a uniform length `L//2` of mass `M_(1)` and a uniform length `L//2` of mass `M_(2)`,
The `M.I` of rod about an axis passing through the geometrical center and `bot^(ar)` to length03:22View SolutionFour spheres each of mass `M` and diameter `2r`, are placed with their centers on the four corners of a square of side `a( gt 2r)`. The moment of inertia of the system about one side of the square is
04:29View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
04:10View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. it is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
 03:46View Solution
03:46View SolutionFrom a circular disc of mass `M` and radius `R`, a part of `60^(@)` is removed. The `M.I.` of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
 02:34View Solution
02:34View SolutionA rod of length`L` and mass `M_(0)` is bent to form a semicircular ring as shown. The `M.I.` about `X'X` is
 01:57View Solution
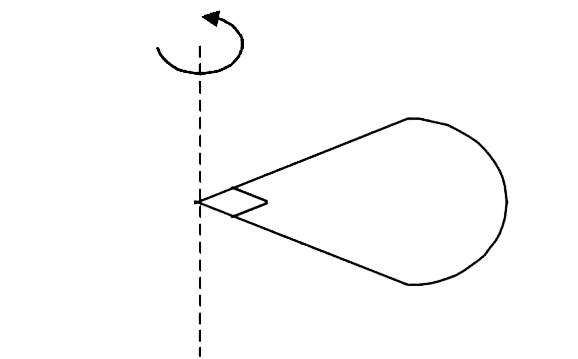
01:57View SolutionA thin wire of length `L` and uniform linear mass density `rho` is bent into a circular loop with centre at `O` as shown. The moment of inertia of the loop about the axis `XX'` is :
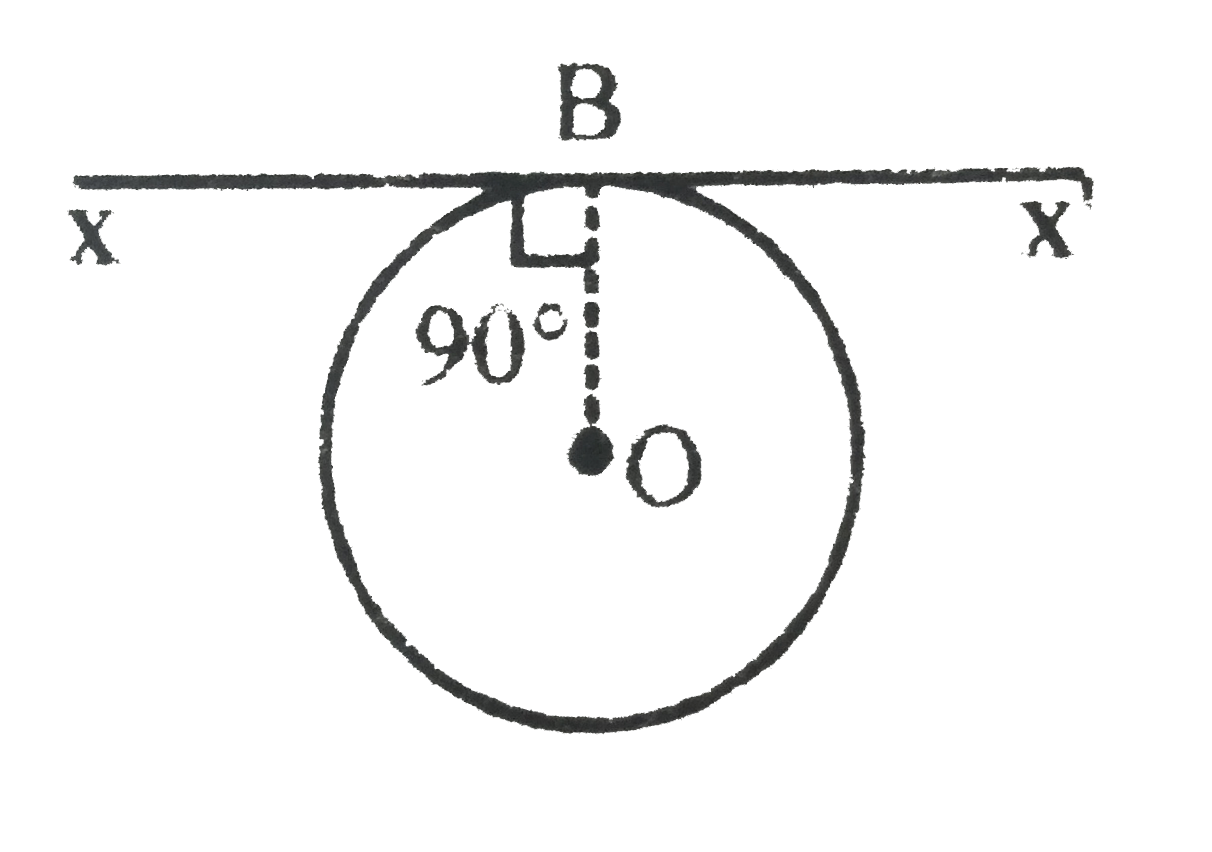 .02:01View Solution
.02:01View SolutionA circular disc is to be made by using iron and aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
02:13View SolutionFour thin rods of same mass `m` and same length `L` form a square as shown in the figure. `M.I.` of this system about an axis through center `O` and perpendicular to its plane is
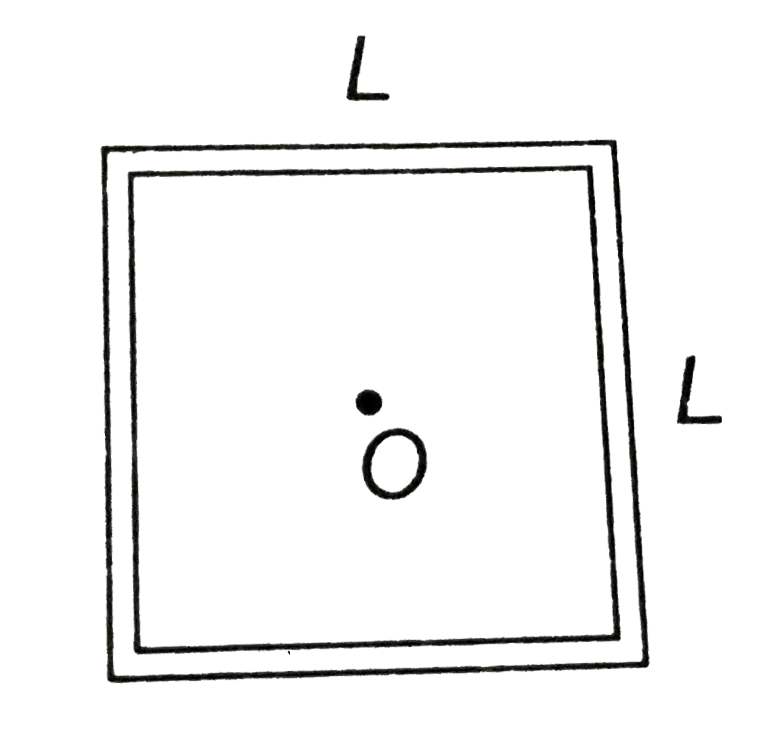 02:39View Solution
02:39View SolutionFour identical rods each of mass `m` and length `l` are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
07:42View SolutionLet `I` be the moment of interia of a uniform square plate about an axis `AB` that passses through its centre and is parallel to two its sides. `CD` is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with `AB`. The moment of inertia of the plate about the axis `CD` is then equal to-
01:58View SolutionThe moment of inertia of thin square plate `ABCD` of uniform thickness about an axis passing through the center `O` and perpendicular to the plane of the plate is
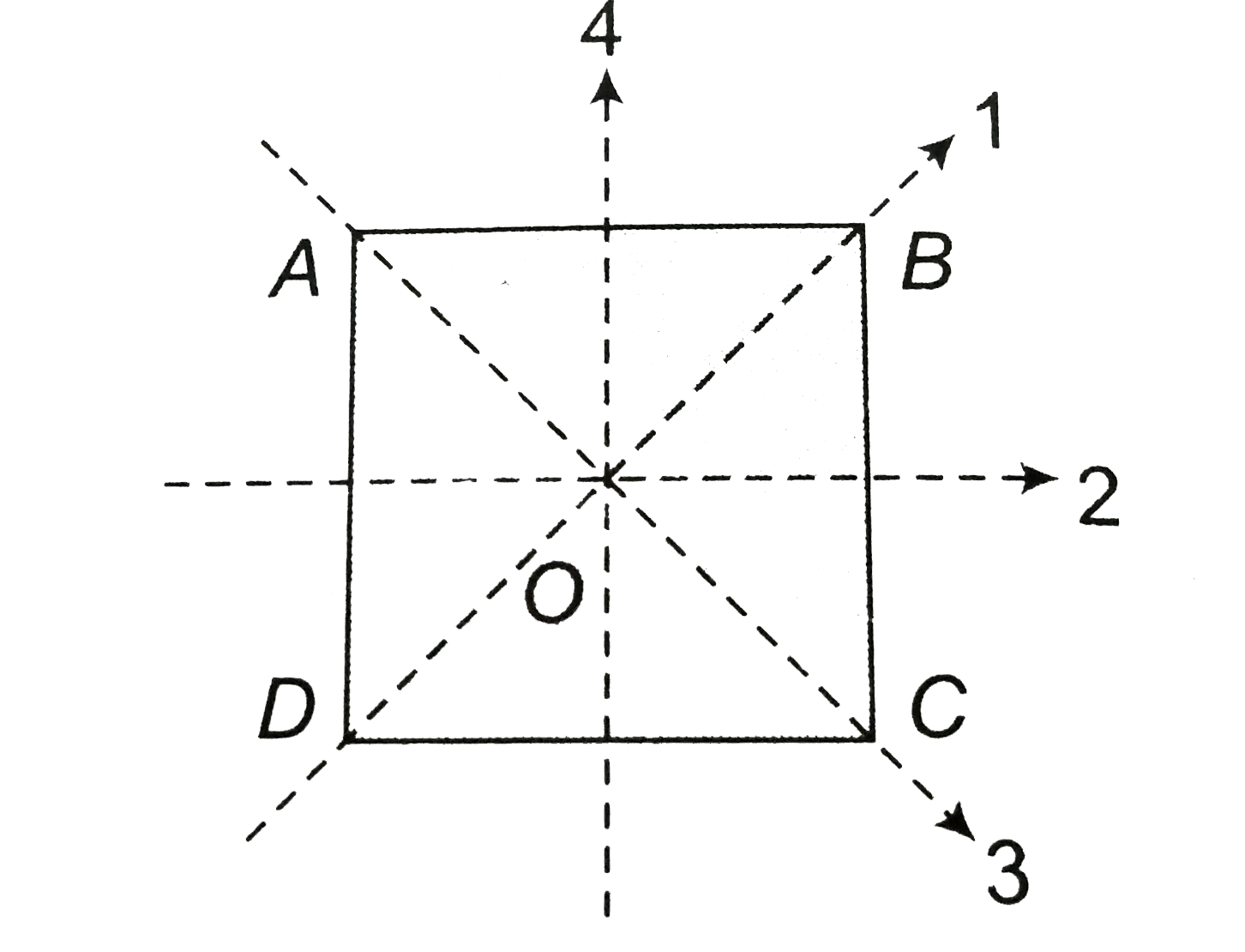
(`i`) `I_(1)+I_(2)`
(`ii`) `I_(2)+I_(4)`
(`iii`) `I_(1)+I_(3)`
(`iv`) `I_(1)+I_(2)+I_(3)+I_(4)`
where `I_(1)`, `I_(2)`, `I_(3)` and `I_(4)` are repectively moments of inertia about axes `1`, `2`, `3` and `4` which are in the plane of the plane03:42View SolutionConsider a uniform square plate of of side and mass `m`. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
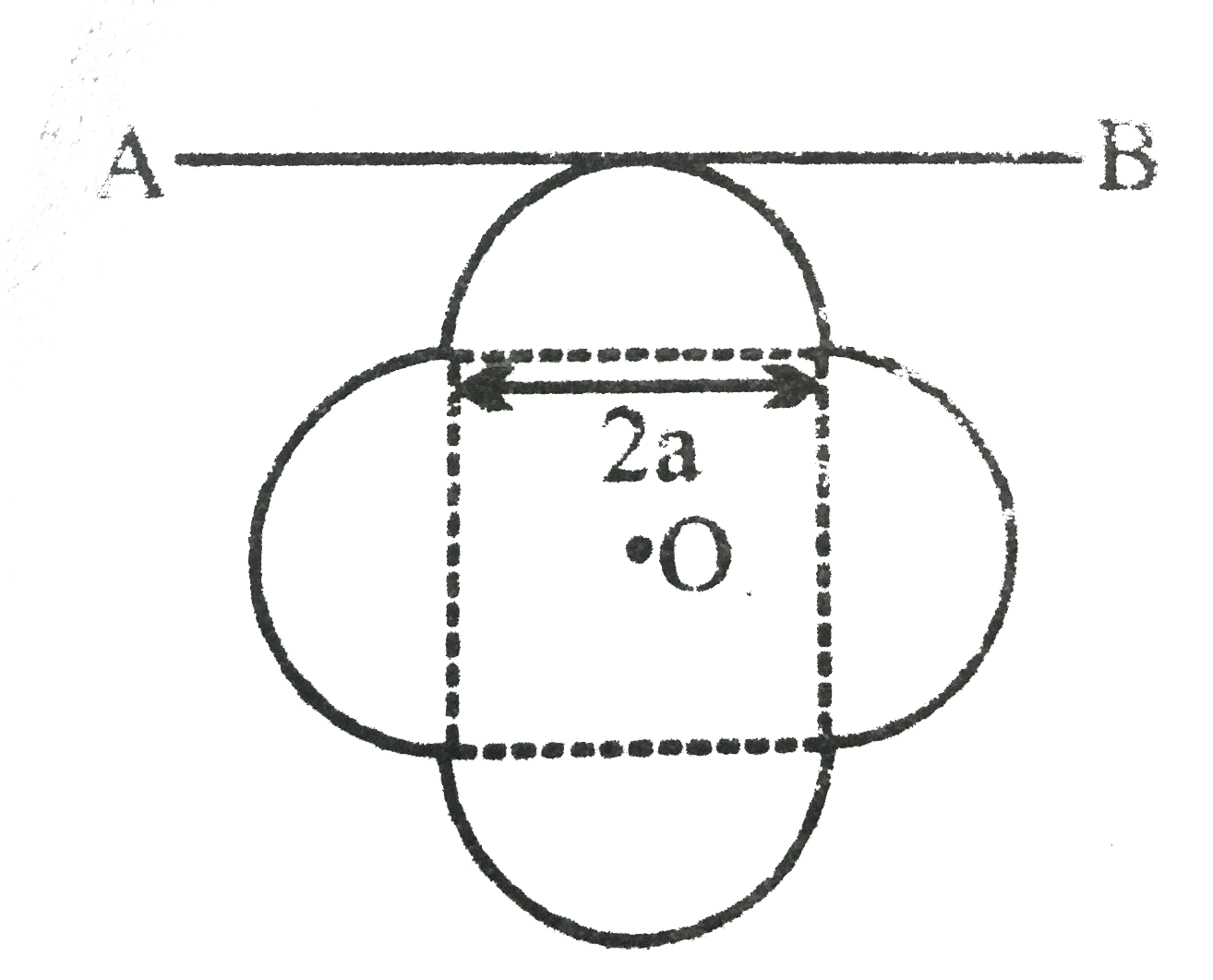
01:06View SolutionA symmetric lamina of mass `M` consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is `2 a`.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is `1.6 Ma^(2)`. The moment of inertia of the lamina about the tangent `AB` in the plane of lamina is.
 .02:26View Solution
.02:26View SolutionFor the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body.
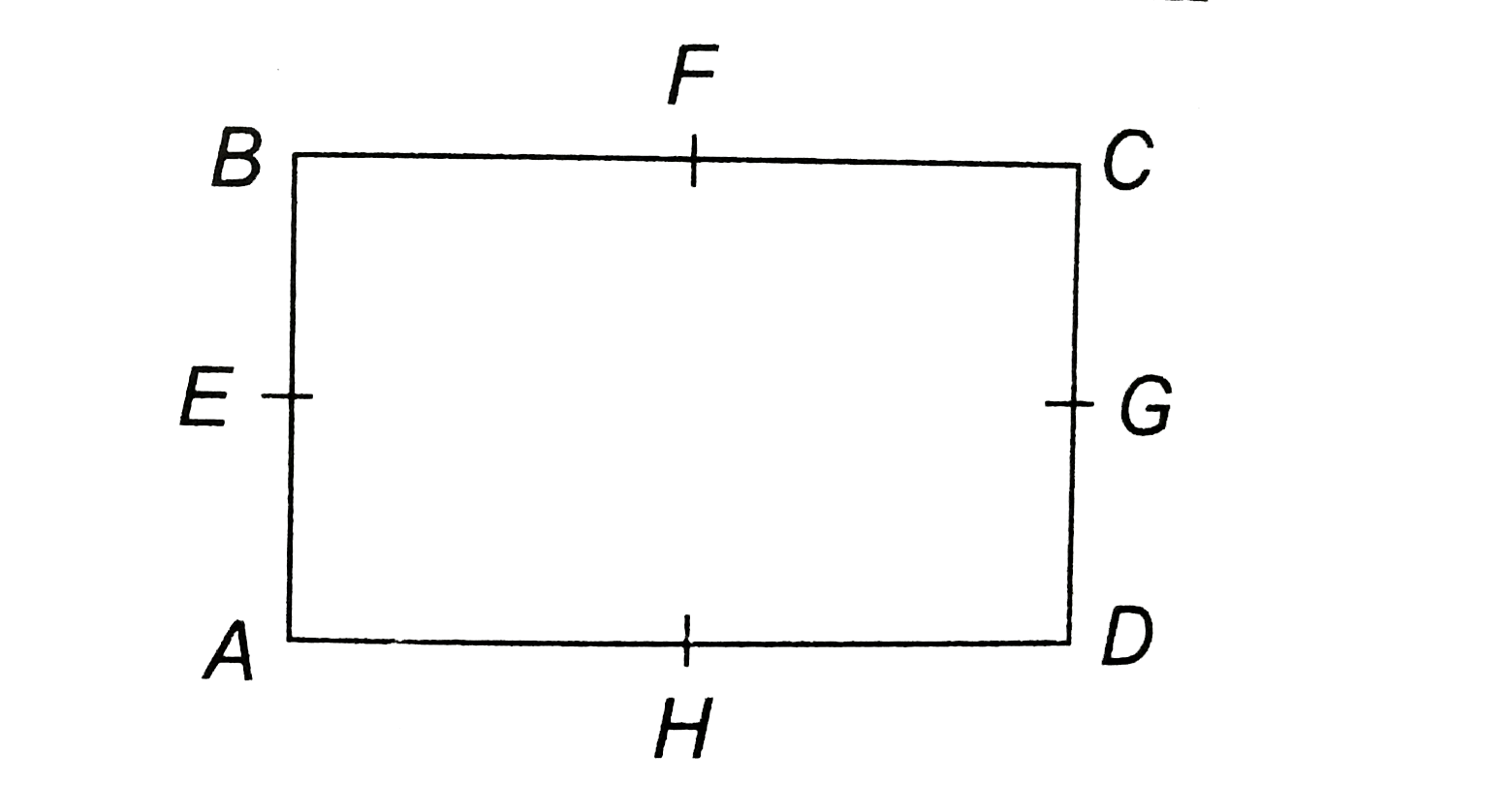
02:22View SolutionIn a rectangle `ABCD` (`BC=2 AB`). The moment of inertia along which the axis will be minimum
 08:20View Solution
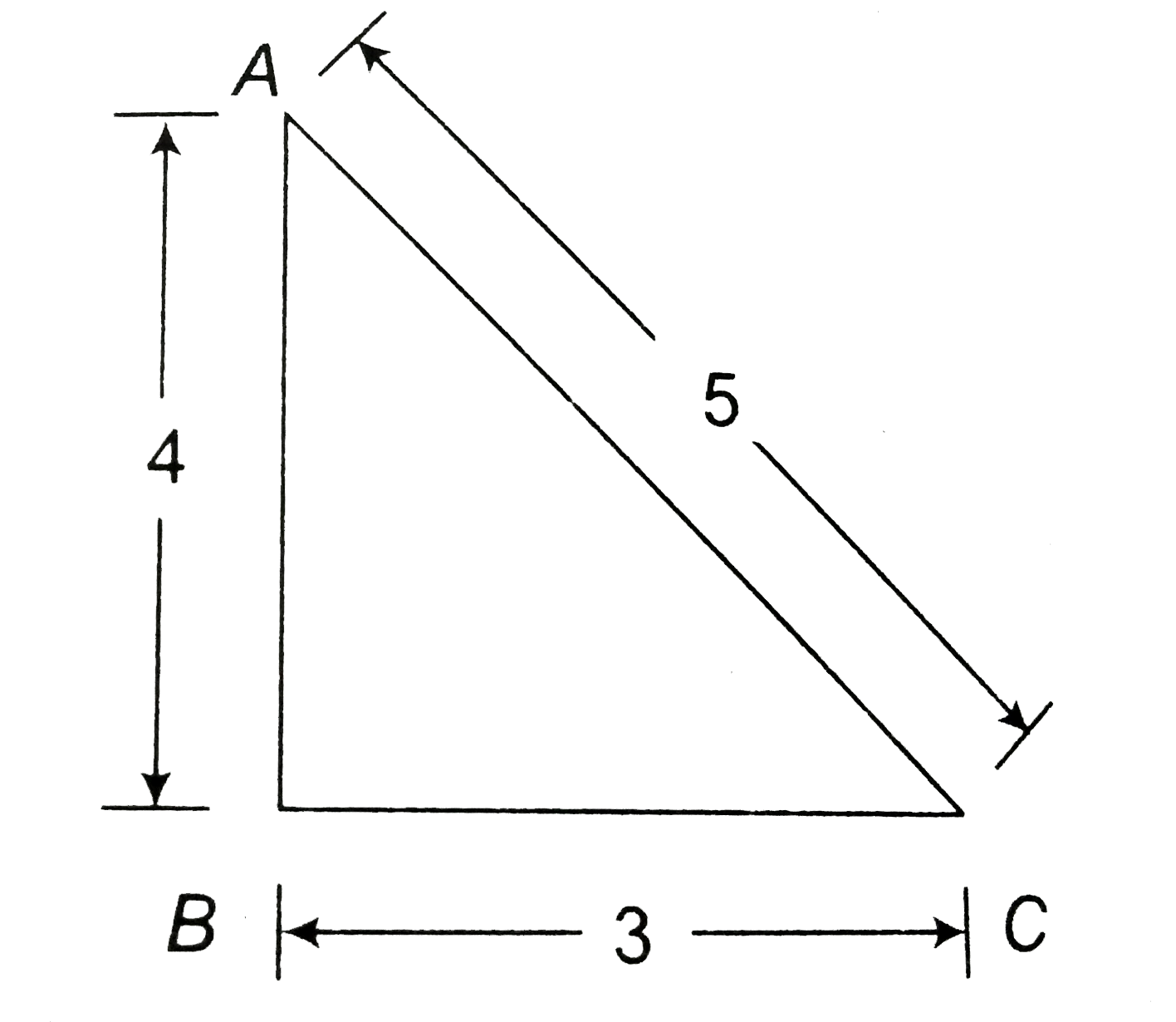
08:20View Solution`ABC` is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. `I_(AB)`, `I_(BC)` and `I_(CA)` are the moments of inertia of the plate about `AB`, `BC` and `CA` repectively. Which one of the following relations is correct?
 06:32View Solution
06:32View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 02:44View Solution
02:44View SolutionA disc of mass `m` and radius `R` has a concentric hole of radius `r`. Its moment of inertia about an axis through its center and perpendicular to its plane is
05:29View SolutionThree identical rods, each of length `L`, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing thorugh a corner and perpendicular to plane of triangle is
05:06View SolutionA ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
01:42View SolutionA flywheel rotates with a uniform angular acceleration. Its angular speed increases from `2pirad//s` to `10pirad//s` in `4 s`. Find the number of revolutions in this period.
02:41View SolutionA fan is making `600` revolutions per minute. If after some time it makes `1200` revolutions per minute, then the increase in its angular velocity is
02:09View SolutionA wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
02:05View SolutionWhen a celling fan is switched off, its angular velocity falls to half while it makes `36` rotations. How many more rotations will it make before coming to rest ?
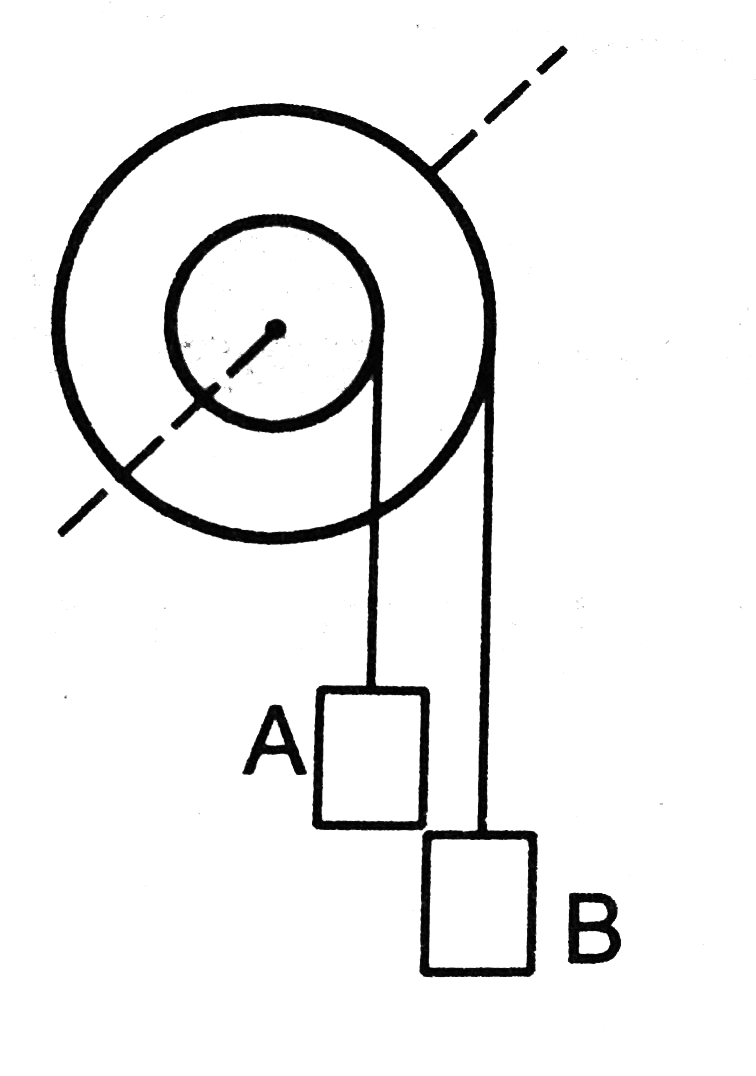
02:51View SolutionFigure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then
 02:47View Solution
02:47View SolutionThe angle turned by a body undergoing circular motion depends on time as `theta=theta_(0)+theta_(1) t+theta_(2)r^(2)`. Then the angular acceleration of the body is
01:25View SolutionIf the equation for the displacement of a particle moving in a circular path is given by `(theta)=2t^(3)+0.5`, where `theta` is in radians and `t` in seconds, then the angular velocity of particle after `2 s` from its start is
01:24View SolutionA flywheel rotates about an axis. Due to friction at the axis, it experiences an angular retardation proportional to its angular velocity. If its angular velocity falls to half while it makes `n` rotations, how many more rotations will it make before coming to rest?
04:50View SolutionA wheel rotates about an axis passing through the center and perpendicular to the plane with slowly increasing angular speed. Then it has
02:40View SolutionA point `p` moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length `s = t^(3) + 5 ` , where `s` is in metres and ` t` is in seconds . The radius of the path is `20 m` . The acceleration of 'P' when ` t = 2 s` is nearly .
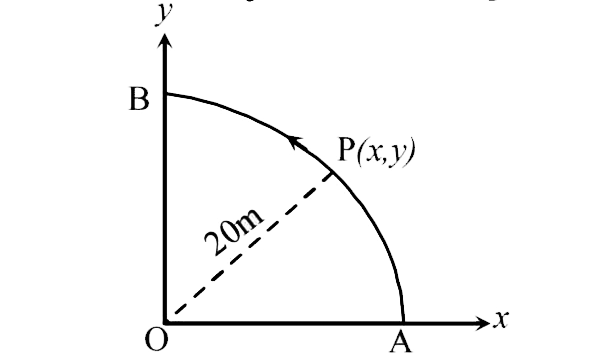 04:18View Solution
04:18View SolutionFind the torque of a force `vecF= -3hati+hatj+5hatk ` acting at the point `vecr=7hati+3hatj+hatk`
02:23View SolutionA force of `-Fhatk` acts on O, the origin of the coodinate system. The torque about the point (1,-1) is
 04:31View Solution
04:31View SolutionA couple produces.
01:20View SolutionLet `vecF` be a force acting on a particle having positon vector `vecr. Let vecr` be the torque of this force about the origin then
02:13View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
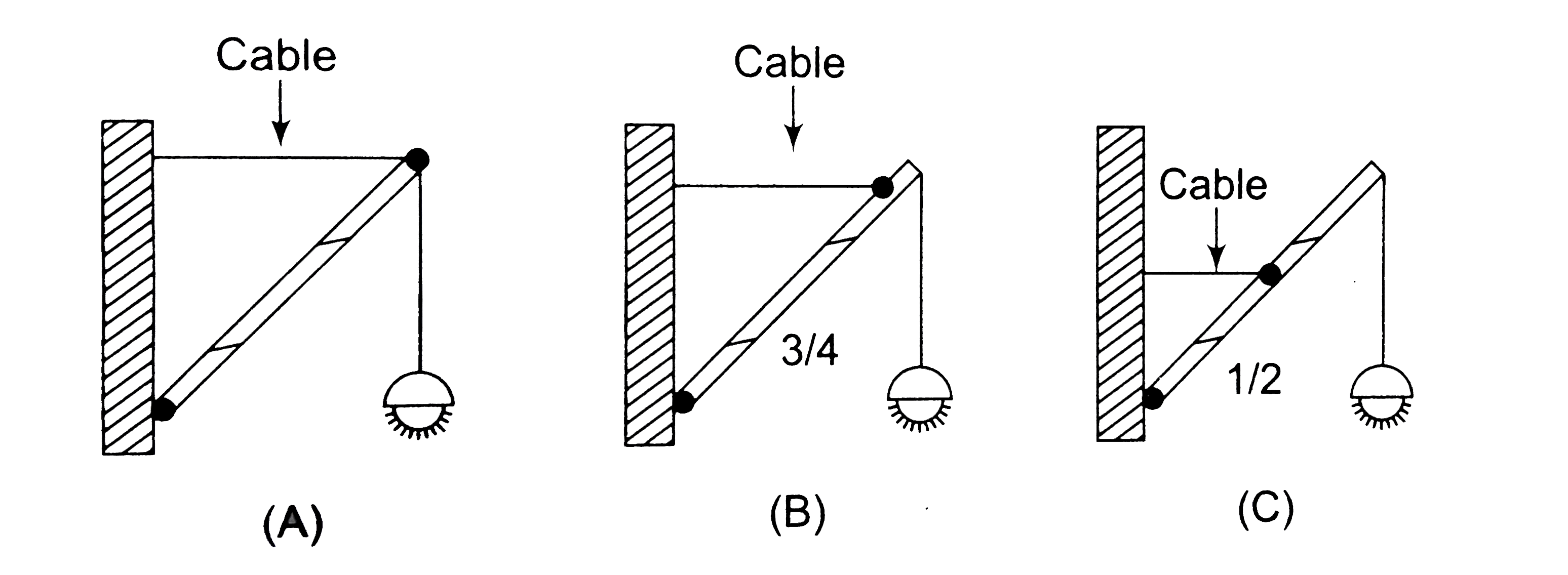 02:27View Solution
02:27View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation
`theta(t) = 2t^(3) - 6 t^(2)`
The torque on the wheel becomes zero at01:35View SolutionA constant torque of `31.4 N-m` id exterted on a pivoted wheel. If the angular acceleration of the wheel is `4 pi rad//s^2`, then the moment of inertia will be.
01:11View SolutionA string is wound round the rim of a mounted flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel in `rad//s^(2)` is
02:54View SolutionA wheel having moment of inertia `2 kg m^(2)` about its vertical axis, rotates at the rate of `60 rpm` about this axis. The torque which can stop the wheel's rotation in one minute would be
03:01View SolutionA flywheel of moment of inertia `I` is rotating with uniform angular speed `omega`. If a torque `tau` retards the wheel, then the time in which the wheel comes to rest is
01:43View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 J`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
02:24View SolutionA wheel of radius `0.4m` can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of `4 kg` is hung. An angular acceleration of `8 rad//s^(2)` is produced in it due to the torque. Then, the moment of inertia of the wheel is (`g=10m//s^(2)`)
 03:35View Solution
03:35View SolutionA mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
02:09View SolutionIn the previous problem, the tension in the string is
View SolutionA uniform rod of length `l` and mass `m` is free to rotate in a vertical plane about `A` as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 04:02View Solution
04:02View SolutionTwo men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
07:01View SolutionIn first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at `A` and a force is applied at the steel and at `O`. On second figure the stick is pivoted at the steel end at `O` and the same force is applied at the wooden end at `A`. The angular acceleration.
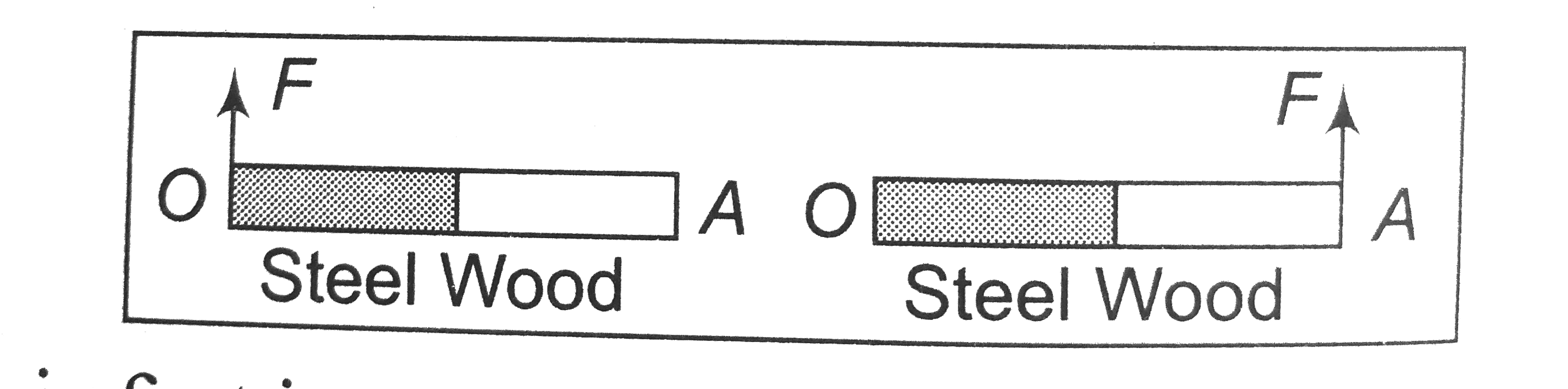 .02:24View Solution
.02:24View SolutionThe density of as rod graduallly decreases from one end to the other. It is pivoted at an end so that ilt can move about a vertical axius through the pivot. A horizontal force F is applied on the free end n a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted are
02:57View SolutionA circular disc `A` of radius `r` is made from an iron plate of thickness `t` and another circular disc `B` of radius `4r` is made from an iron plate of thickness `t//4`. Equal torques act on the discs `A` and `B`, initially both being at rest. At a later instant, the linear speeds of a point on the rim of `A` and another point on the rim of `B` are `v_(A)` and `v_(B)`, respectively. We have
08:20View SolutionA pulley os radius 2m is rotated about its axis by a force `F= (20 t- 5t^2)` newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is `10kg m^2` the number of rotaitons made by the pulley before its direction of motion is reversed, is:
02:33View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
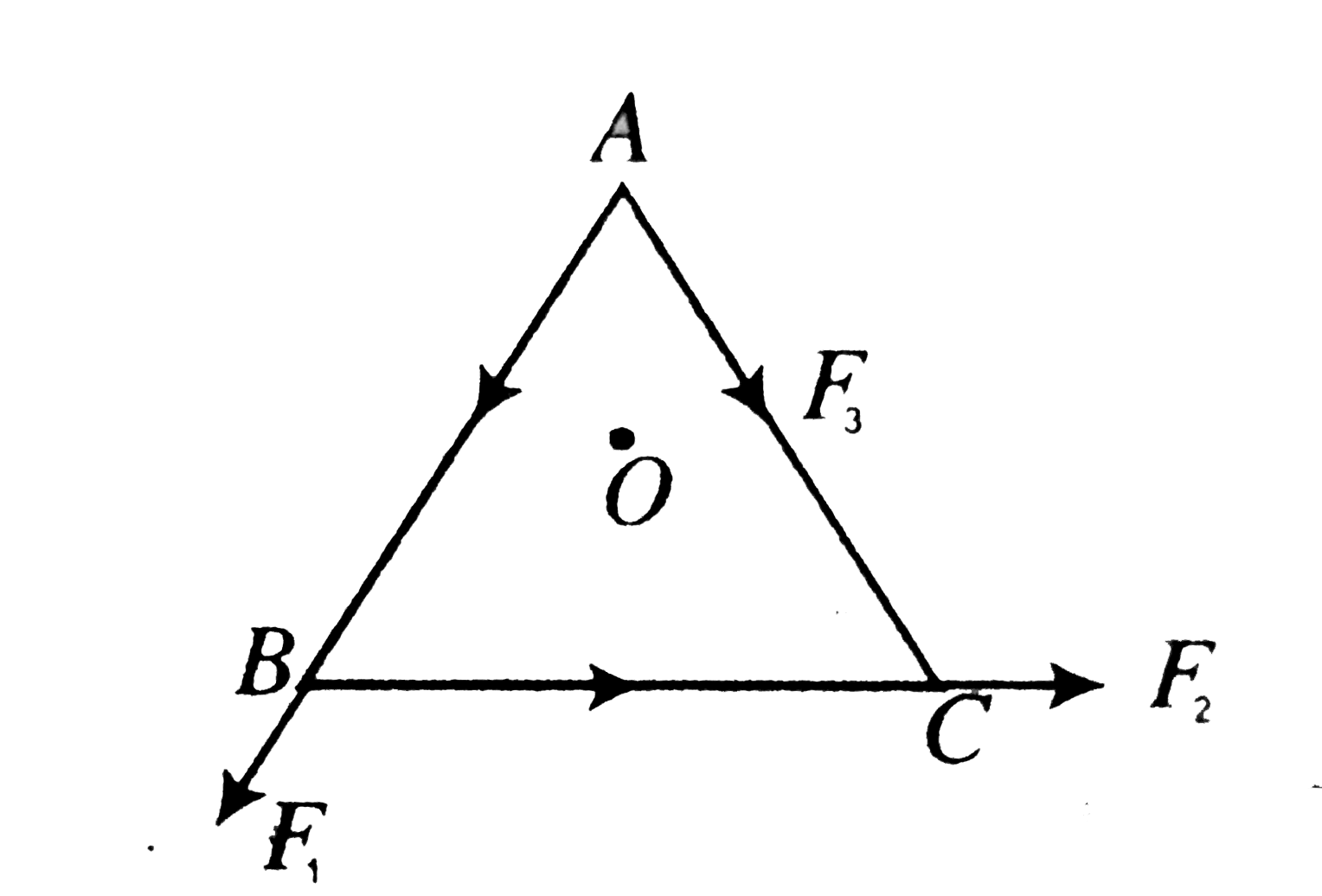 02:31View Solution
02:31View SolutionFor a system to be in equilibrium, the torques acting on it must balance. This is true only if the torques are taken about
01:53View SolutionTwo men `A` and `B` are carrying a uniform bar of length `L` on their shoulders. The bar is held horizontally such that A gets one-fourth load. If `A` is at one end of the bar, the distance of `B` from that end is
04:30View SolutionA uniform horizontal meter scale of mass `m` is suspended by two vertical strings attached to its two ends. A block of mass `3m` is placed on the `60 cm` mark. The tensions in the two strings are in the ratio
05:20View SolutionThe line of action of the resultant of two like parallel forces shifts by one-third of the distance between the forces when the two forces are interchanged. The ratio of the two forces is
05:52View SolutionIf a ladder weighting `250 N` is placed against a smooth vertical wall having coefficient of friction between it and floor 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor?
02:06View SolutionA ladder rests against a frictionless vertical wall, with its upper end `6 m` above the ground and the lower end `4 m` away from the wall. The weight of the ladder is `500 N` and its `CG` at `1//3^(rd)` distance from the lower end. Wall's reaction will be (in newton)
04:25View SolutionA cyckist moves along a curved road with a velocity `v`. The road is banked for speed `v`. The angle of banking is `theta`. Which of the following statement is not true?
03:24View SolutionA cyclist moves around a circular path of radius `40sqrt3 m` with a speed of `20 m//s`. He must lean inwards at an angle `theta` with the vertical such that `tan theta` is equal to
02:34View SolutionA car is moving on a circular path and takes a turn. If `R_(1)` and `R_(2)` be the reactions on the inner and outer wheels, respectively, then
03:08View SolutionA car sometimes overturns while taking a turn. When it overturns, it is
02:47View SolutionA rectangular block has a square base measuring `axxa` and its height is `h`. It moves on a horizontal surface in a direction perpendicular to one of the edges. The coefficient of friction is `mu`. It will topple if
03:43View SolutionA block of base `10cmxx10cm` and height 15cm is kept on an inclined plane. The coefficient of friction between them is `sqrt3`. The inclination `theta` of this inclined plane from the horizontal plane is gradually increased from `0^@` Then
04:53View SolutionA rod of length `L`, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
04:03View SolutionA uniform rod of length `L` is placed with one end in contact with the horizontal and is then inclined at an angle `alpha` to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
03:18View SolutionA cord is wound round the circumference of wheel of radius `r`. The axis of the wheel is horizontal and fixed and moment of inertia about it is `I`. A weight `mg` is attached to the end of the cord and falls from rest. After falling through a distance `h`, the angular velocity of the wheel will be.
03:35View SolutionA uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
02:41View SolutionAn automobile engine develops `100` kilo`-`watt, when rotating at a speed of `1800 rev//min`. Find the torque developed by it.
01:44View SolutionA flywheel is in the form of a uniform circular disc of radius `1 m` and mass `2 kg`. The work which must be done on it to increase its frequency of rotation from `5` to `10 rev//s` is approximately
03:47View SolutionTwo point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
06:28View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a unifrom angular velocity `omega`. Theforce exerted by the clamp on the rod has a horizontal component
04:19View SolutionA particle of mass `m` moves along line `PC` with velocity `v` as shown. What is the angular momentum of the particle about `O`?
 01:45View Solution
01:45View SolutionIn an orbital motion, the angular momentum vector is :
01:23View SolutionThe position of a particle is given by `vecr=(hati+2hatj-hatk)` and momentum `vecp=(3hati+4hatj-2hatk)`. The angular momentum is perpendicular to the
02:19View SolutionA unit mass at position vector `vecr=(3hati+hatj)` is moving with velocity `vecv=(5hati-6hatj)`. What is the angular momentum of the body about the origin?
01:56View SolutionA mass M moving with a constant velocity parlale to the X-axis. Its angular momentum with respect to the origin
01:31View SolutionIf the particle of mass `m` is moving with constant velocity `v` parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect to origin at any time `t`.
 03:27View Solution
03:27View SolutionA particle of mass `m` moves in the `XY` plane with a velocity `v` along the straight line `AB`. If the angular momentum of the particle with respect to origin `O` is `L_(A)` when it is at A and `L_(B)` when it is at B, then
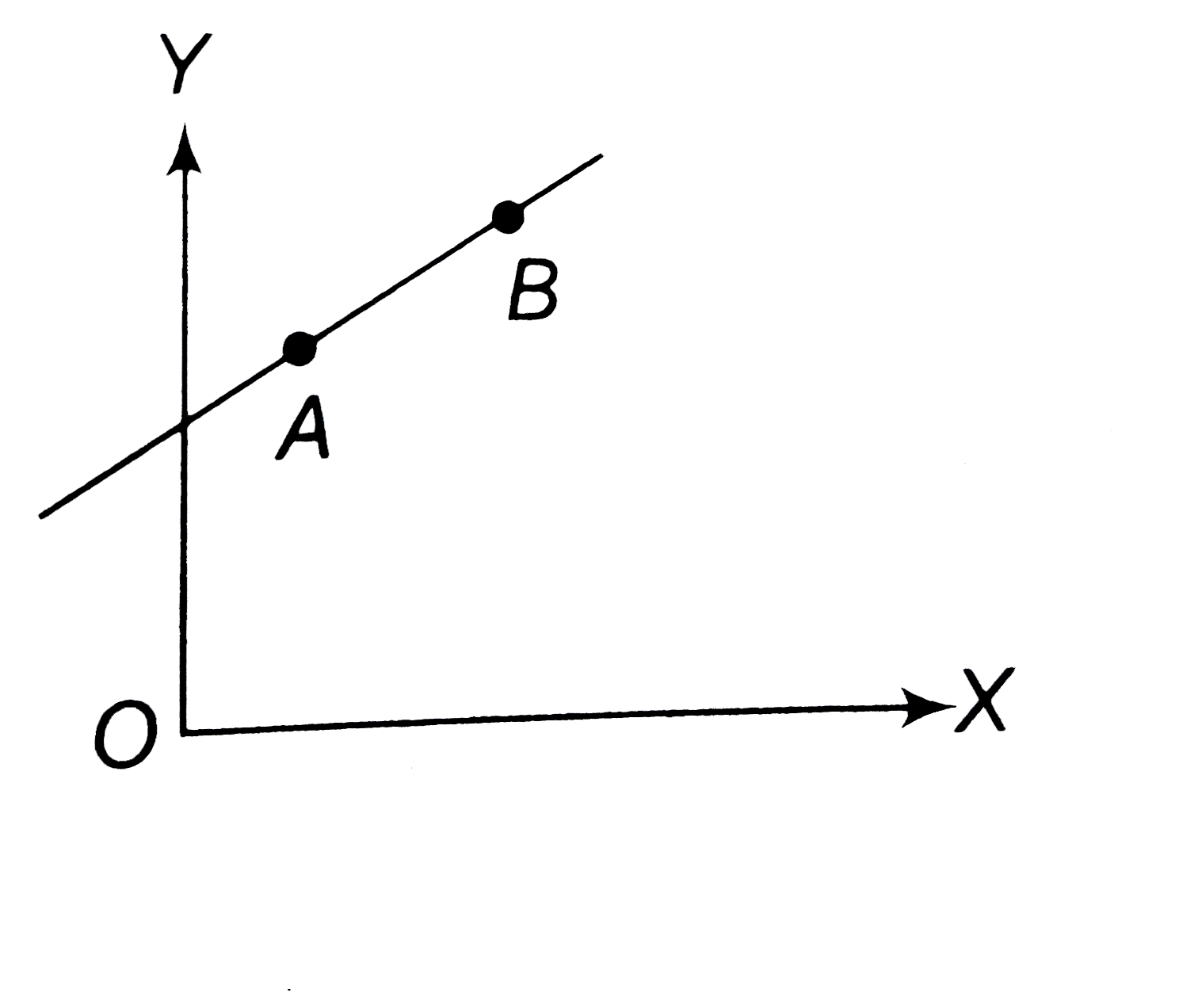 03:06View Solution
03:06View SolutionA particle of mass `5g` is moving with a uniform speed of `3sqrt2 cm//s` in the `x-y` plane along the line `y=x+4`. The magnitude of its angular momentum about the origin in `g cm^(2)//s` is
04:21View SolutionA particle of mass m is projected with a velocity v making an angle of `45^@` with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
07:00View SolutionA small particle of mass ` m` is projected at an angle `theta` with the ` x`- axis with an initial velocity ` v_(0)` in the ` x-y `plane as shown in the figure . At a time ` t lt ( v_(0) sin theta)/(g) `, the angular momentum of the particle is
where `hat (i) , hat (j) and hat(k)` are unit vectors along `x , y and z` - axis respectively.
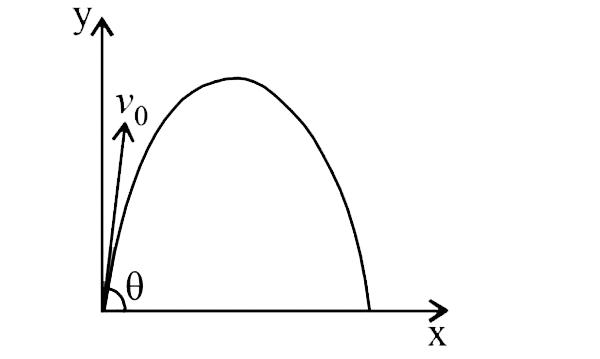 06:42View Solution
06:42View SolutionA particle performing uniform circular motion gas angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
01:36View SolutionTwo bodies have their moments of inertia `I` and `2 I` respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
01:48View Solution
Exercise questions and complete solutions for chapter ROTATIONAL MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11
