Complete Solutions to Example of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| CP SINGH | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Three particles `A`,`B` and `C` of masses `m`,`2m` and `3m` are placed on a straight line of length `2L` as shown. Find the `M.I.` about an axis passing through `B` and perpendicular to the line `AC`.
View SolutionTwo particles of masses `m` and `2m` are placed at separation `L`. Find the `M.I.` about an axis passing through the center of mass and perpendicular to the line joining the point masses.
View SolutionThree particles each of mass `m` are placed on the vertices of an equilateral triangle of length `L`. Find the `M.I`.
(`a`) about an axis passing through
(`i`) one particle and perpendicular to the plane
(`ii`) mid-point of the side of triangle and `bot^(ar)` to the plane
(`iii`) center of triangle and `bot^(ar)` to the plane
(`b`) (`i`) an axis coinciding with side of triangle
(`ii`) about median of triangle
View SolutionThree thin, uniform, indentical rods each or mass `M` and length `L` are joined as shown. Find the `M.I.` about an axis passing through `O` and perpendicular to the plane.
View SolutionFind the `M.I.`
(`a`) An axis passing through `A` and `bot^(ar)` to the length.

(`b`) (i)An axis passing through the perimeter of ring and `bot^(ar)` to the plane.

(ii) An axis touching the perimeter and lying in the same the plane.
(`c`) Solid sphere

An axis touching the sphere (tangential axes)
(`d`) An uniform disc
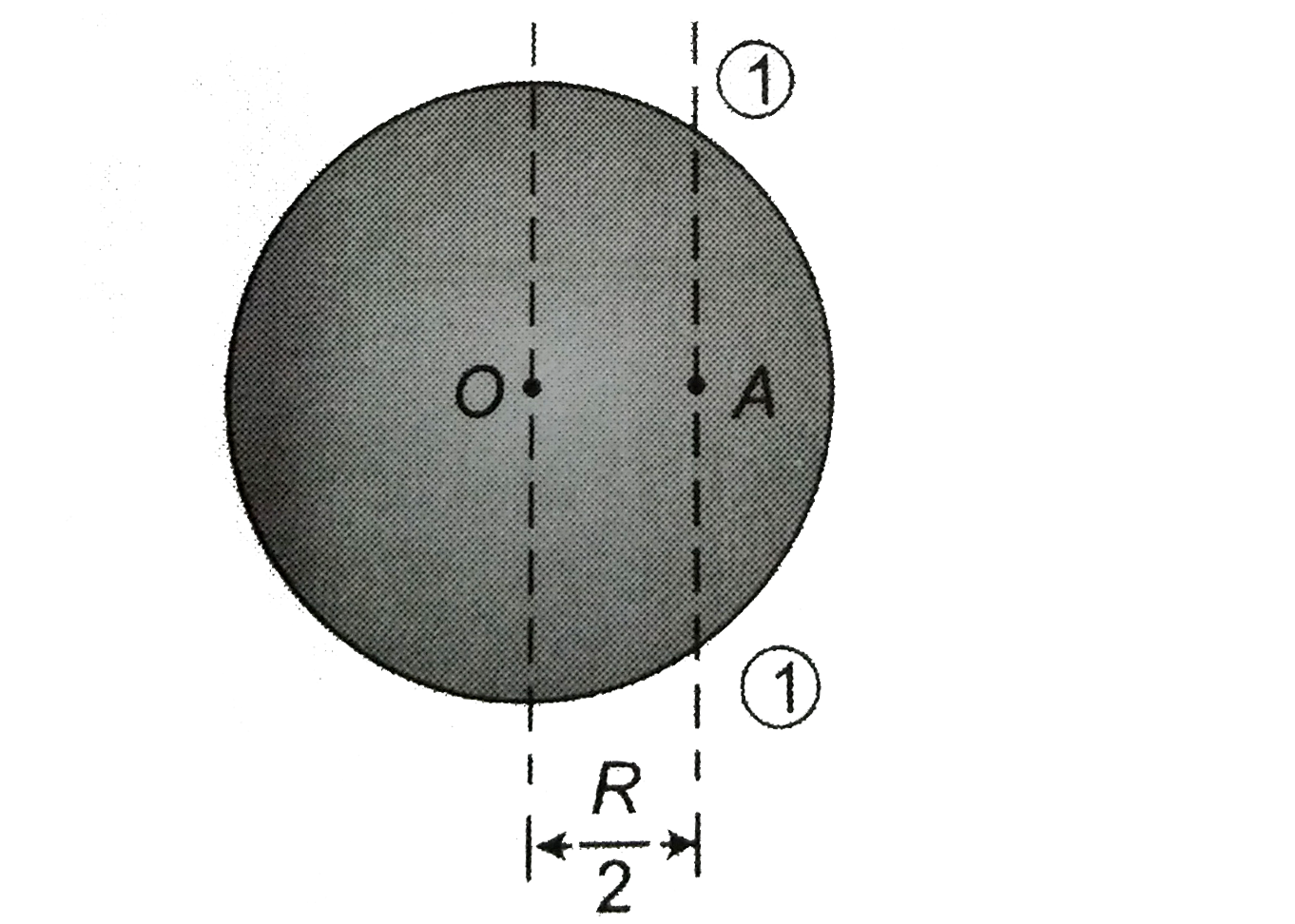
An axis passing through `A`, parallel to the diameter and lying in the same plane.
View SolutionFour identical spheres each of mass `M` and radius `R` are placed on the vertices of a square of edge `L`. Find the `M.I.` about an axis
(`a`) coinciding with the side of a square and
(`b`) coinciding with the diagonal of a square.
View SolutionThree identical roads each of mass `M` and `L` are joined to form an equilateral triangle. Find the `M.I.` about an axis perpendicular to the plane of triangle and passing through
(`a`) center of triangle
(`b`) mid-point of a rod and
(`c` ) one vertex of triangle.
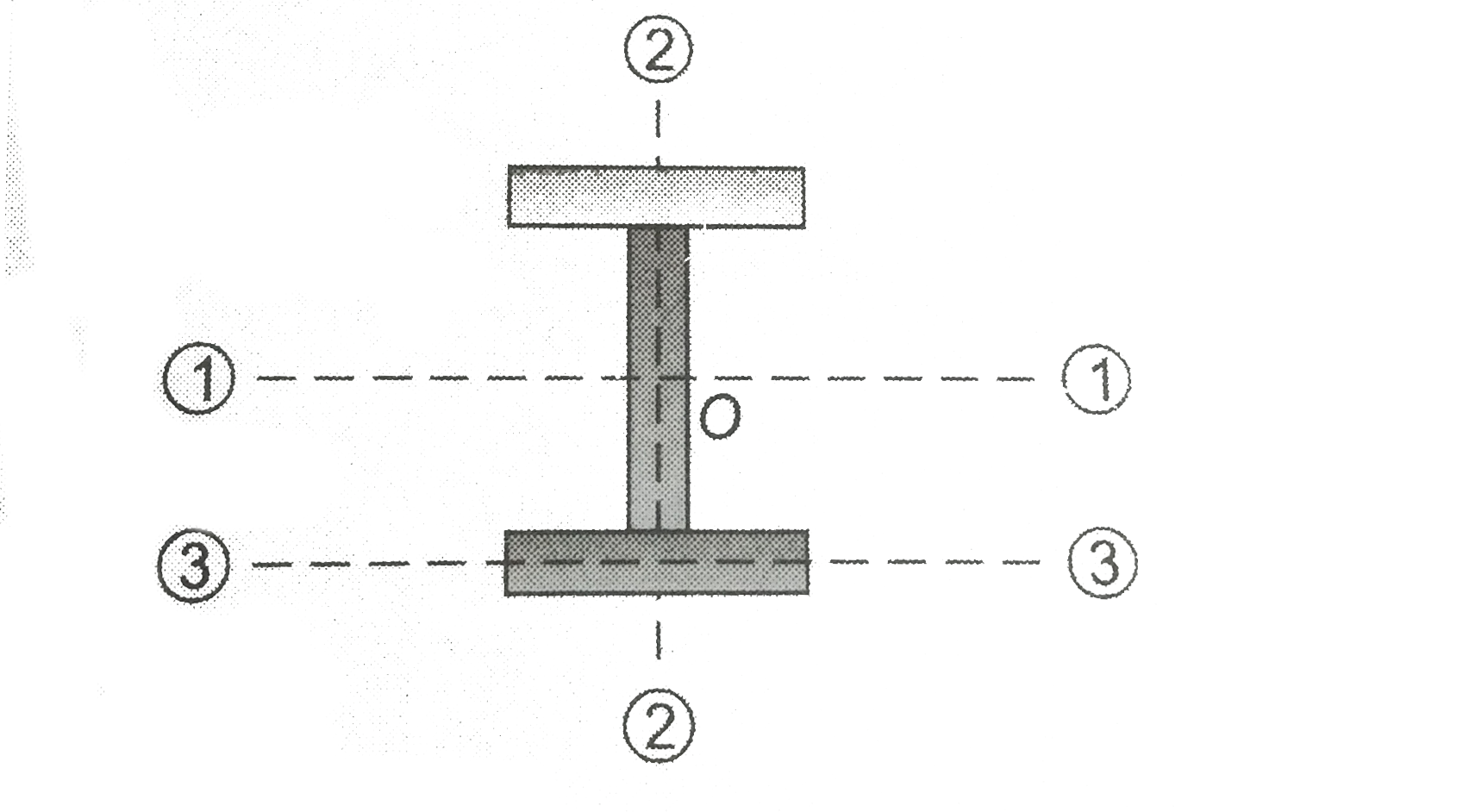
View SolutionThe three rods of the previous problem are connected symmetrically as shown. Find the `M.I.` about `(1)-(1), (2)-(2)` and `(3)-(3)`
View SolutionThree thin unifrom circular discs each of mass `M` and radius `R` are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the `M.I.` about an axis passing through the center of mass system of discs and perpendicular to the plane.
View SolutionFrom a thin uniform disc of radius `2R`. Another disc of diameter `2R` is removed. The mass of the remaining portion is `m`. Find the `M.I.` of the shaded portion about an axis passing through `O` and pependicular to the plane.
View SolutionFrom a disc of radius `r_(1)`, a concentric disc of radius `r_(2)` is removed . The mass of the remaining portion is `m`. Find the `M.I.` of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View SolutionTwo thin uniform rods `A` (`M.L`) and `B` (`3M,3L`) are joined as shown. Find the `M.I.` about an axis passing through the center of mass of system of rods and perpendicular to the length.

View SolutionTwo thin uniform rings made of same material and of radii `R` and `4 R` are joined as shown. The mass of smaller ring is `m`. Find the `M.I.` about an axis passing through the center of mass of system of rings and perpendicular to the plane.
View SolutionFind the momentof inertia of a uniform square plate of mass m and edge a about one of its diagonals.
View SolutionFour identical rods each of mass `m` and length `L` are joined to form a square. Find the `M.I.` about
(a) the `x`-axis,
(b) the `y`-axis,
(c) the `z`-axis,
(d) about `1-1`,
(e) an axis passing through one corner and perpendicular to the plane.
View SolutionFind the `M.I.` of thin uniform rod of mass `M` and length `L` about the axis as shown.

View SolutionThe linear mass density (i.e. Mass per unit length) of a rod of length `L` is given by `rho=rho_(0)(x)/(L)`, where `rho_(0)` is constant and `x` is the distance from one end `A`. Find the `M.I.` about an axis passing through `A` and perpendicular to length of rod. Express your answer in terms of mass of rod `M` and length `L`.
View SolutionFind the `M.I.`

View SolutionThe radius of gyration of an uniform rod of length `l` about an axis passing through one of its ends and perpendicular to its length is.
View SolutionFind the radius of gyration of a system of particles about an axis passing through the center of mass and perpendicular to the line joining the particles. The system consists of two particles of masses `m_(1)` and `m_(2)` placed at separation at `r`
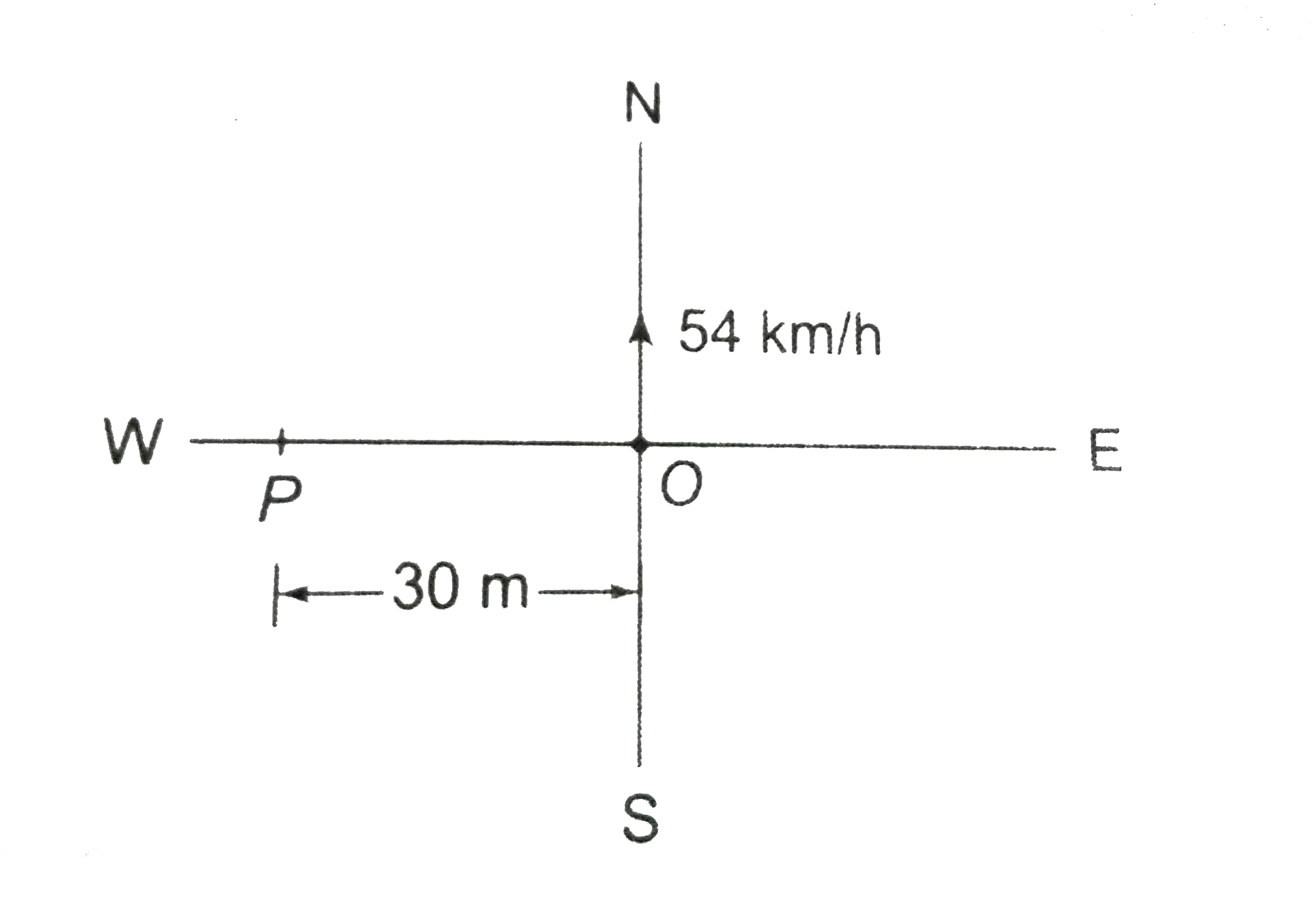
View SolutionA verticle is moving due north with an absolute velocity `54 km//h`. An observer at `P` is at distance `30 m` to the west of the line of travel. What is the angular velocity of vehicle relative to the observer at `t=0` and `t=2 s`.
View SolutionAs shown, there is rotating spotlight at a perpendicular distance `h` from a horizontal floor. The light revolves at `N rev//min` about a horizontal axis perpendicular to the paper. Find the velocity of light spot traveling along the floor.
View SolutionA flywheel rotates with a uniform angular acceleration. Its angular speed increases from `2pirad//s` to `10pirad//s` in `4 s`. Find the number of revolutions in this period.
View SolutionWhen a fan is switched on, it makes `10` rotations in the first `2 s`. How many rotations will it make in the next `2 s`, assuming uniform angular acceleration?
View SolutionA wheel rotates under constant angular acceleration starting from rest. Find the ratio of angle rotated in `n second` and `n^(th) second`.
View SolutionA wheel starting from rest is uniformely accelerated at `2 rad//s^(2)` for `5 s`. It is allowed to rotated uniformly for the next `10 s` and is finally brought to rest in the next `5 s`. Find the total angle rotated by the wheel.
View SolutionA wheel of radius `15 cm` is rotating about its axis at angluar speed of `20 rad//s`. Find the linear speed and total acceleration of a point on the rim.
View SolutionA disc rotates about its axis with a constant angular accelertion of `2 rad//s^(2)`. Find the radial and tangential accelerations of a particle at a distance of `10 cm` from the axis at the end of the fourth second after the disc starts rotating.
View SolutionA uniform rod of length `L` is rotating about its one end in the horizontal plane under constant aceeleration `alpha` starting from rest. Find the linear velocity of its mid-point after time `t_(0)`. Also, find the normal and tangential components of acceleration of the mid-point of the rod at this instant.
View SolutionA particle A moves along a circle of radius `R=50cm` so that its radius vector r relative to the point O(figure) rotates with the constant angular velocity `omega=0.40rad//s`. Find the modulus of the velocity of the particle, and the modulus and direction of its total acceleration.

View SolutionThe angular position of a swinging door is described by `theta=5+10t+20t^(2)`. Determine the angular position, angular speed and angular acceleration at `t=2 s`.
View SolutionThe angular position of a point on the rim of a rotating wheel is given by `theta=4t^(3)-2t^(2)+5t+3` rad. Find
(a) the angular velocity at `t=1 s`,
(b) the angular acceleration at `t=2 s`.
(c ) the average angular velocity in time interval `t=0` to `t=2 s` and
(d) the average angular acceleration in time interval `t=1` to `t=3 s`.
View SolutionA solid body rotates about a stationary axis so that the rotation angle `theta` varies with time as `theta=6t-2t^(3)` radian. Find
(a) the angular acceleration at the moment when the body stops and
(b) the average value of angular velocity and angular acceleration averaged over the time interval between `t=0` and the complete stop.
View SolutionA solid body rotates with angular velocity `vecomega=3thati+2t^(2) hatj rad//s`. Find
(a) the magnitude of angular velocity and angular acceleration at time `t=1 s` and
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
View SolutionA roller in a printing press turns through an angle `theta=3t^(2)-t^(3) rad`.
(a) Calculate the angular velocity and angular acceleration as a function of time `t`.
(b) What is the maximum positive angular velocity and at what time `t` does it occur?
View SolutionA particle describes circular motion with its angular displacement `theta` at anytime `t` is given by `theta=5t-3` radian. If the radius of circular path is `2 m`, find the total acceleration of particle.
View SolutionA wheel rotates around a stationary axis so that the rotation angle `theta` varies with time as `theta=2t^(2)` radian. Find the total acceleration of the point `A` at the rim at the moment `t=0.5 s` If the radius of wheel is `1 m`.
View SolutionA solid body starts rotating about a stationary axis with an angular acceleration `alpha=kt`, where `k` is a constant. How soon after the beginning of motion will the total acceleration vector of an arbitrary point of the body form an angle `60^(@)` with its velocity vector?
View SolutionA solid body rotates about a stationary axis so that its angular velocity depends on the rotation angle `varphi` as `omega=omega_0-avarphi`, where `omega_0` and a are positive constants. At the moment `t=0` the angle `varphi=0`. Find the time dependence of
(a) the rotation angle,
(b) the angular velocity.
View SolutionA solid body starts rotating about a stationary axis with an angular acceleration `alpha=alpha_(0) cos theta`, where `alpha_(0)` is a constant and `theta` is an angle of rotation from the initial position. Find the angular velocity of the body as a function of `theta`.
View SolutionA solid body rotates with deceleration about a stationary axis with an angular deceleration `betapropsqrt(omega)`, where `omega` is its angular velocity. Find the mean angular velocity of the body averaged over the whole time of rotation if at the initial moment of time its angular velocity was equal to `omega_0`.
View SolutionCalculate the torque (magnitude and direction) about point `O` due to the forces as shown. In each case, forces and rod lie in the plane of the paper.
(`a`)
(`b`)
(`c` )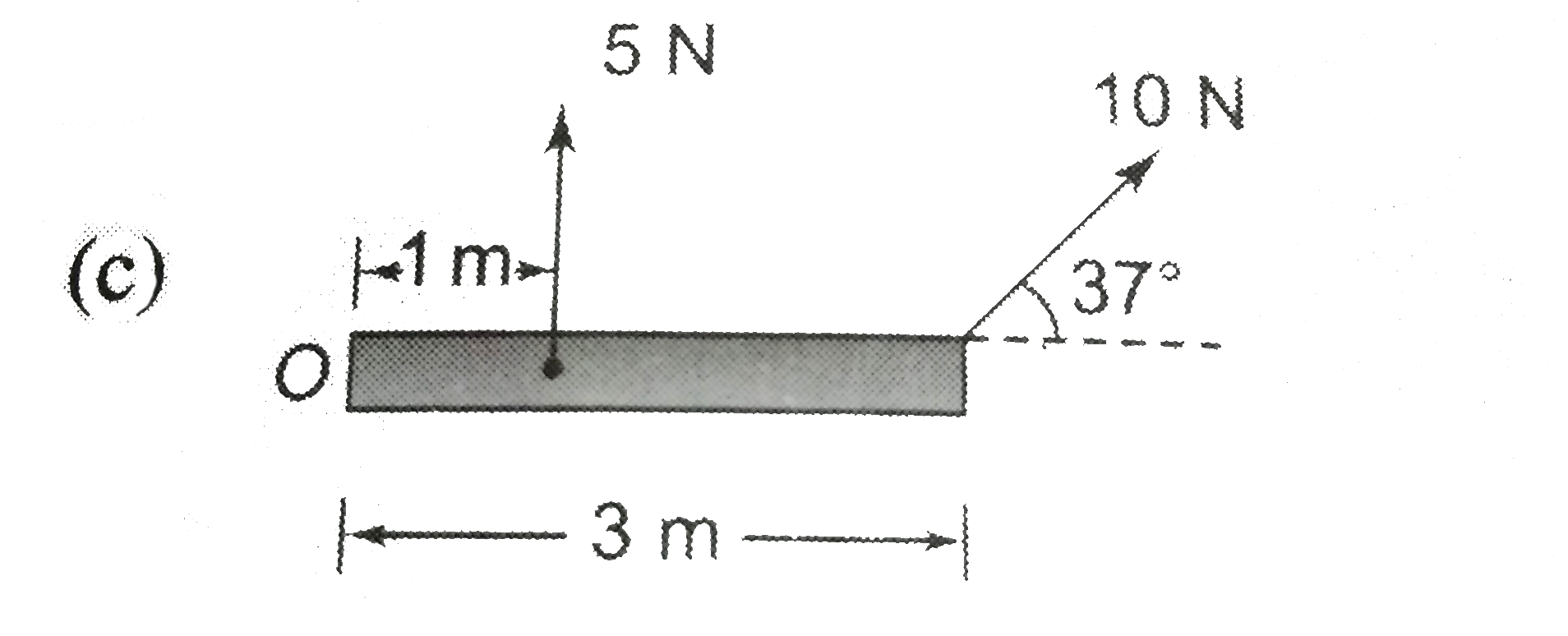
(`d`)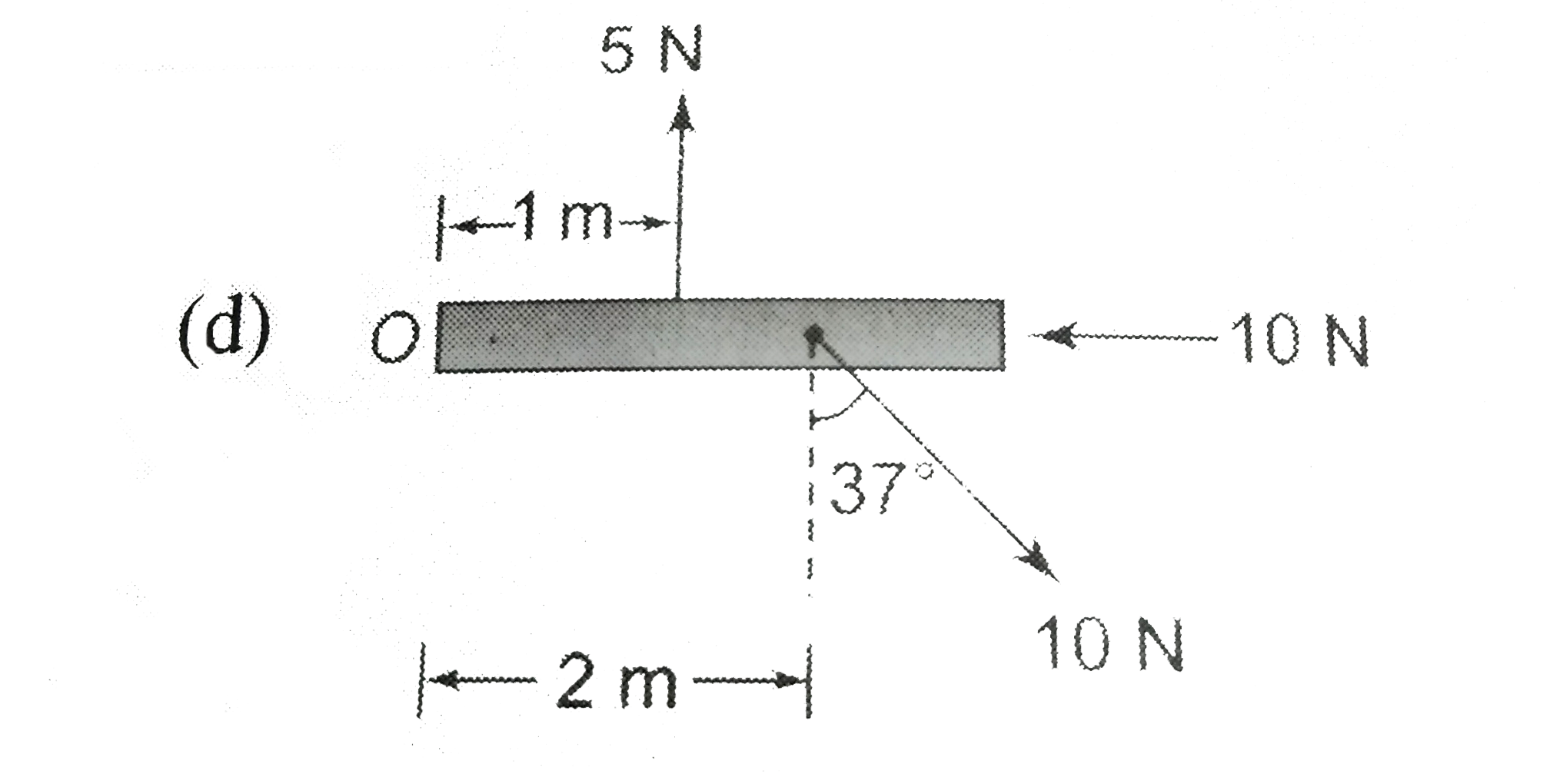
View SolutionFind the torque of forces about `O`
(`a`)
(`b`)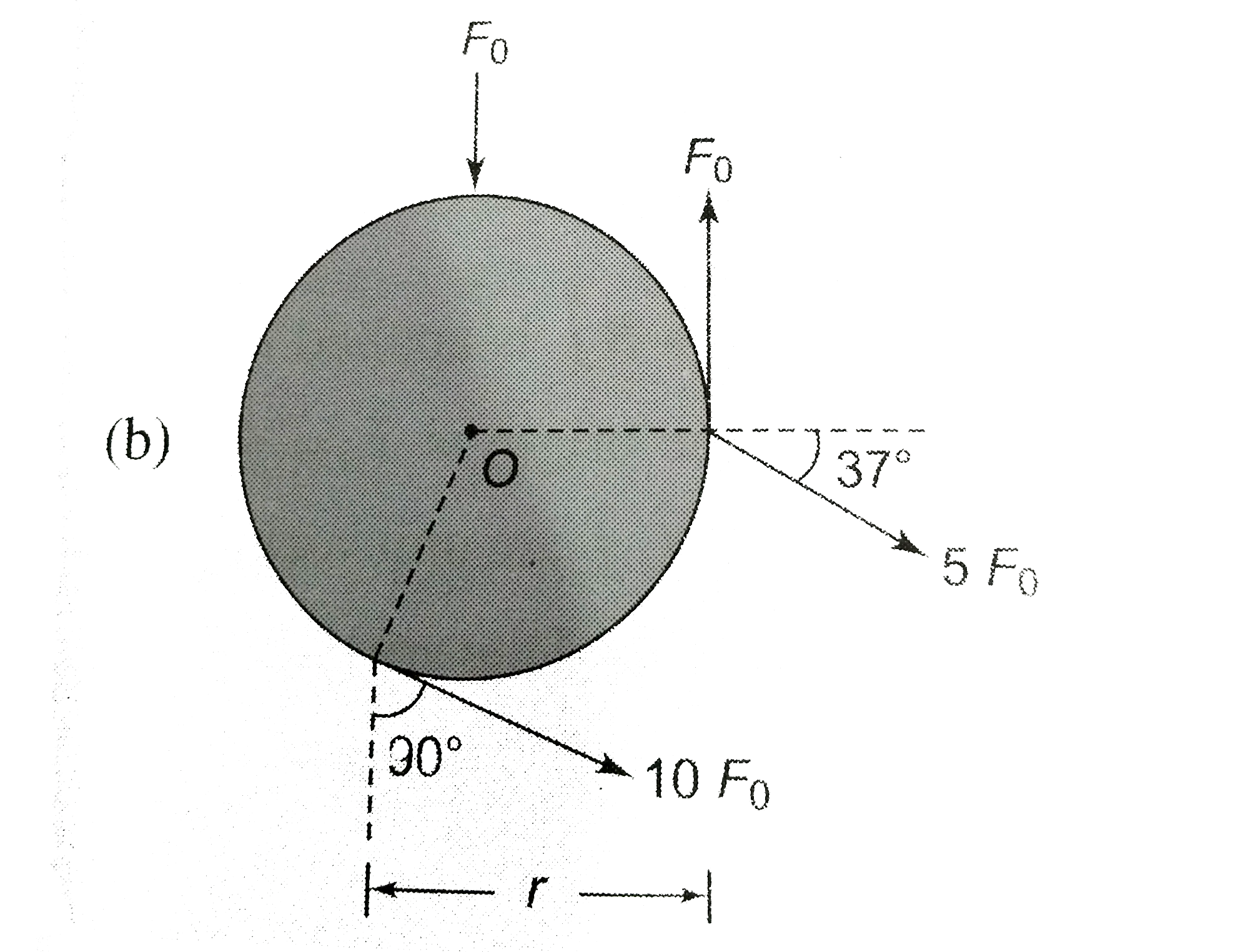
View SolutionFind the total torque acting on the body shown in the figure about the point `O`.
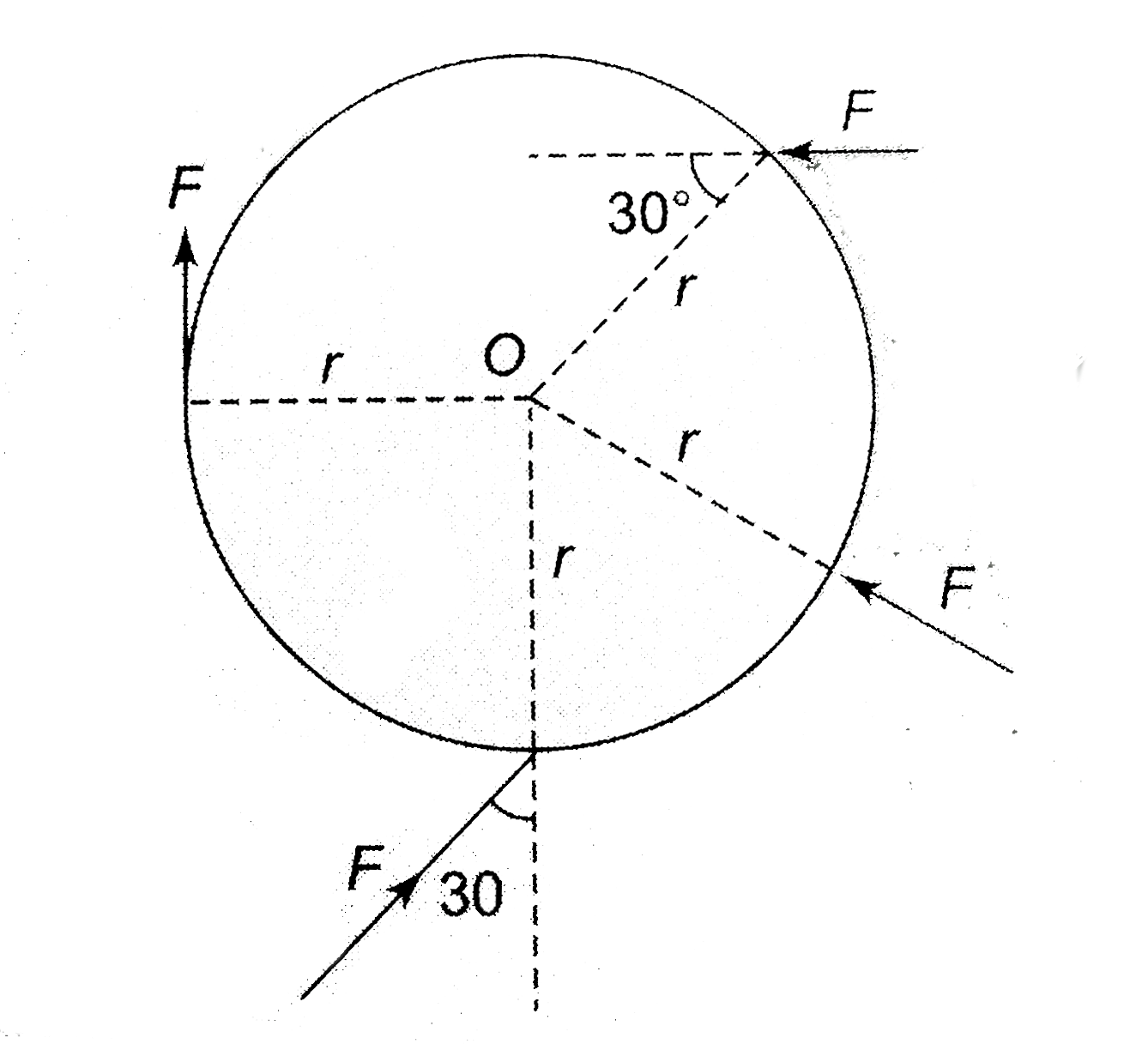
View SolutionA particle of mass `m` is projected with a speed `v_(0)` at an angle of projection `theta` with horizontal. Find the torque of the weight of the particle about the point of projection after time `(v_(0)sintheta)/(g)`
View SolutionA uniform rod of length `L` and mass `M` is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
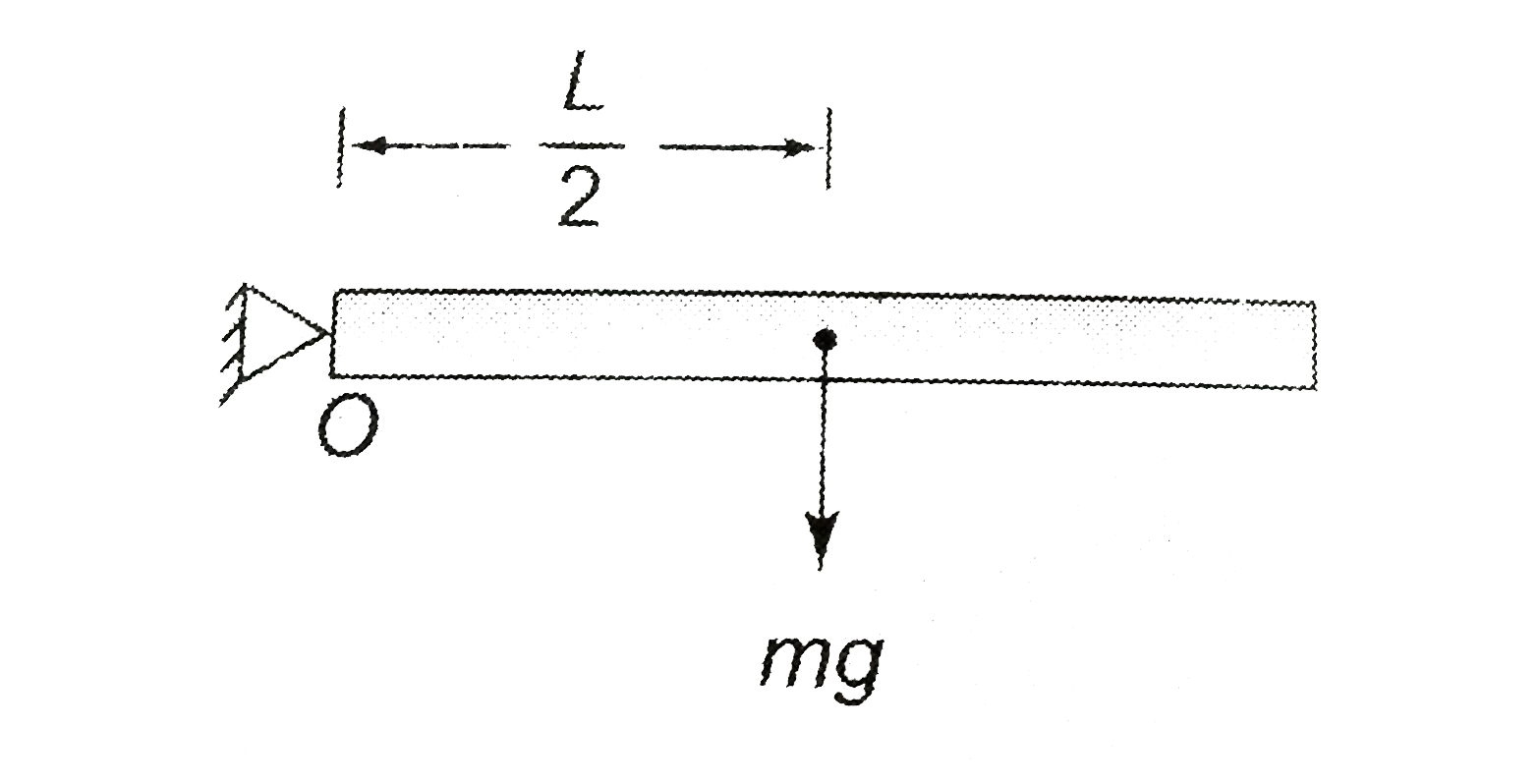
View SolutionFind the torque of a force `vecF=3hati+4hatj+5hatk N` about a point `O`, whose position vector is `vecr = hati+hatj+hatk m`.
View SolutionA force `vecF=Ahati+Bhatj` is applied to a point whose radius vector relative to the origin is `vecr=ahati+bhatj`, where `a`, `b`, `A`,`B` are constants and `hati`, `hatj` are unit vectors along the `X` and `Y` axes. Find the torque `vectau` and the arm `l` of the force `vecF` relative to the point `O`.
View SolutionThree force are applied to a square plate as shown in the figure. Find the magnitude, direction and point of application of the resultant force if this point is taken on the side `BC`.
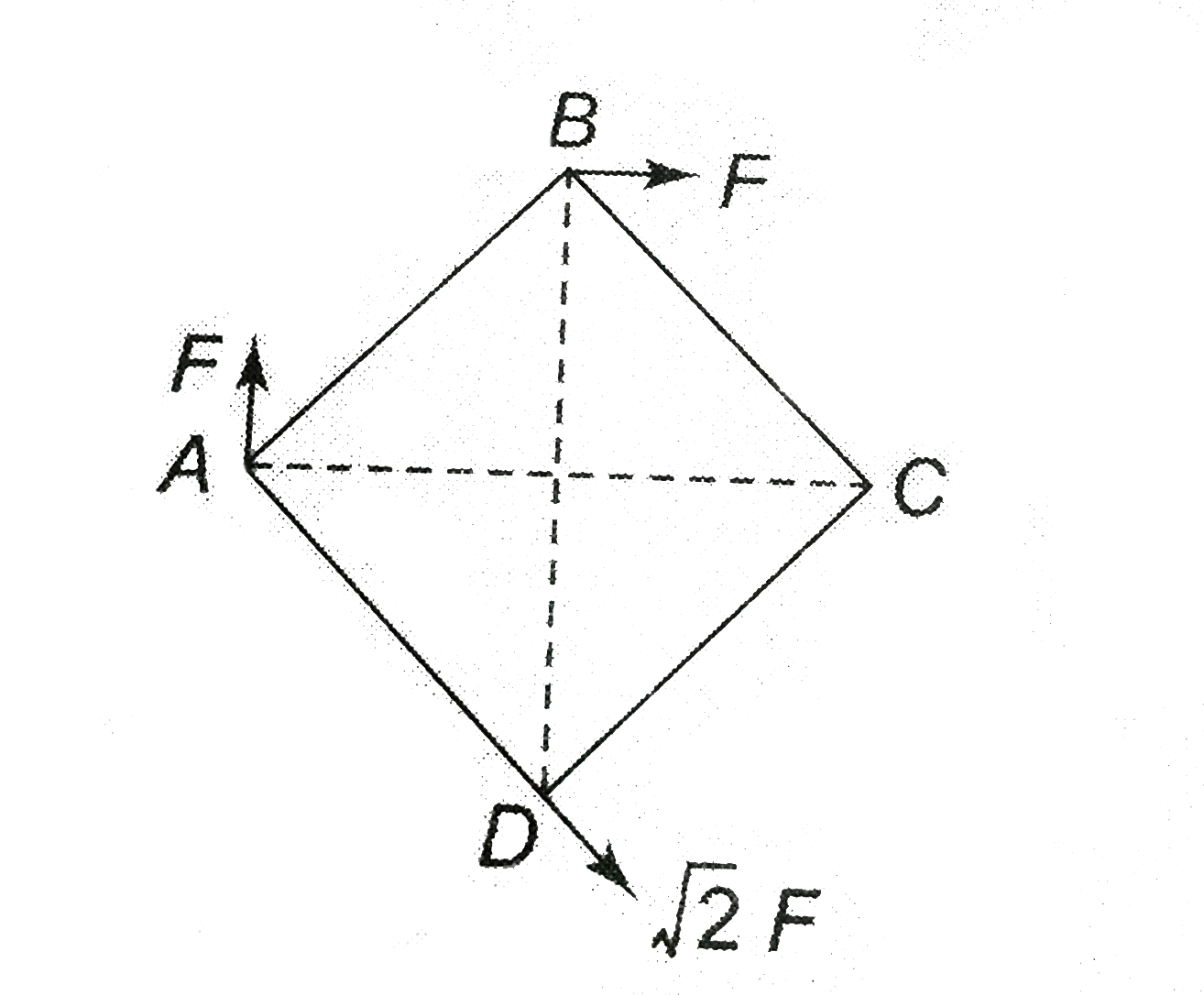
View SolutionA pulley has the shape of a uniform solid disc of mass `2 kg` and radius `0.5 m`. A string is wrapped over its rim and is pulled by a force of `2.5 N`. The pulley is free to rotate about its axis. Initially, the pulley is at rest. Find the angular velocity and angle rotated by pulley in `10 s`.

View SolutionA wheel rotating at a speed of 120 rpm about its axis is brought to rest by applying a constant torque for `4 s`. Find the number of revolutions completed by the wheel before stop.
View SolutionA pulley in the form of solid disc of mass `5kg` and radius `1 m` is rotating at an angular speed of 120 rpm when the motor is turned off, Neglecting the friction at the axle, calculate the force that must by applied tangentially to the pulley to bring it to rest in 4 revolutions.
View SolutionA rod of mass `M` and length `L` lying horizontally is free to rotate about a vertical axis through its end. A horizontal force `F` on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle `pi//2`.
View SolutionConsider the situation as shown in the figure. The moment of inertia of wheel is `2 kg m^(2)` and its radius is `0.25 m`. Find the angular acceleration of the wheel, assuming no slipping.

View SolutionA cylinder of weight `W` and raidus `R` is to be raised onto a horizontal step of height `h=R//3` as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of `F` to raise the cylinder.

View SolutionTwo men support a uniform rod of mass `M` and length `L` at its two ends. If one of them suddenly withdraws, find the force excerted by the rod on the other man
(`a`) immediately after withdrawl and
(`b`) when the rod makes angle `theta` with vertical.
View SolutionA thin horizontal uniform rod `AB` of mass `m` and length `l` can rotate freely about a vertical axis passing through its end `A`. At a certain moment, the end `B` starts experiencing constant force `F` which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle `phi` counted relative to the initial position.
View SolutionAs shown in the figure, two blocks, each of mass `m`, suspended from the ends of a rigid light rod of length `L`. The rod is held horizontally on the fulcrum and then released.
(`a`) Find the initial angular acceleration of the rod.
(`b`) If the mass of rod is also `m` uniformly distributed. find the tension in the strings attached to blocks.

View SolutionTwo masses `2m` and `m` are attached to the ends of the card which passes over a pulley of mass `m` and radius `R`. Calculate the tension in the wire on both sides of the pulley. Assume no slipping.
View SolutionA uniform rod of mass `m` and length `L` is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass `2m` is placed at distance `L//4` from the left end. Find the tensions in the two strings.
View SolutionA uniform rod of mass `M` and length `L` rests on two supports. A ball of mass `m=M//3` is placed at distance `L//8` from the center as shown. Find reactions at supports.

View SolutionA uniform ladder of weight `W` and length `L` is resting between rough floor and smooth vertical wall. The ladder makes an angle `53^(@)` with horizontal. A man of weight `3W` climbs the ladder and stays at distance `L//3` as shown.
(a) Find the normal and friction force on the ladder at its base.
(b) Find the minimum coefficient of the static friction needed to prevent slipping at the base.
View SolutionA uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is `mu_(1)` and between the rod and the wall is `mu_(2)`. Find the angle at which the rod can be leaned without slipping.
View SolutionA Thin uniform rod `AB` of mass `m=1.0kg` moves translationally with acceleration `a=2.0 m//s^(2)` due to two antiparallel forces `F_(1)` and `F_(2)`. The distance between the points at which these forces are applied is equal to `d=20 cm`. Besides, it is known that `F_(2)=5.0 N`. Find the length of the rod.

View SolutionConsider the door of a room of wieght `W` hinged at two points as shown in the diagram. If the magnitude of forces by the hings on the door are equal, find the magnitude of force.
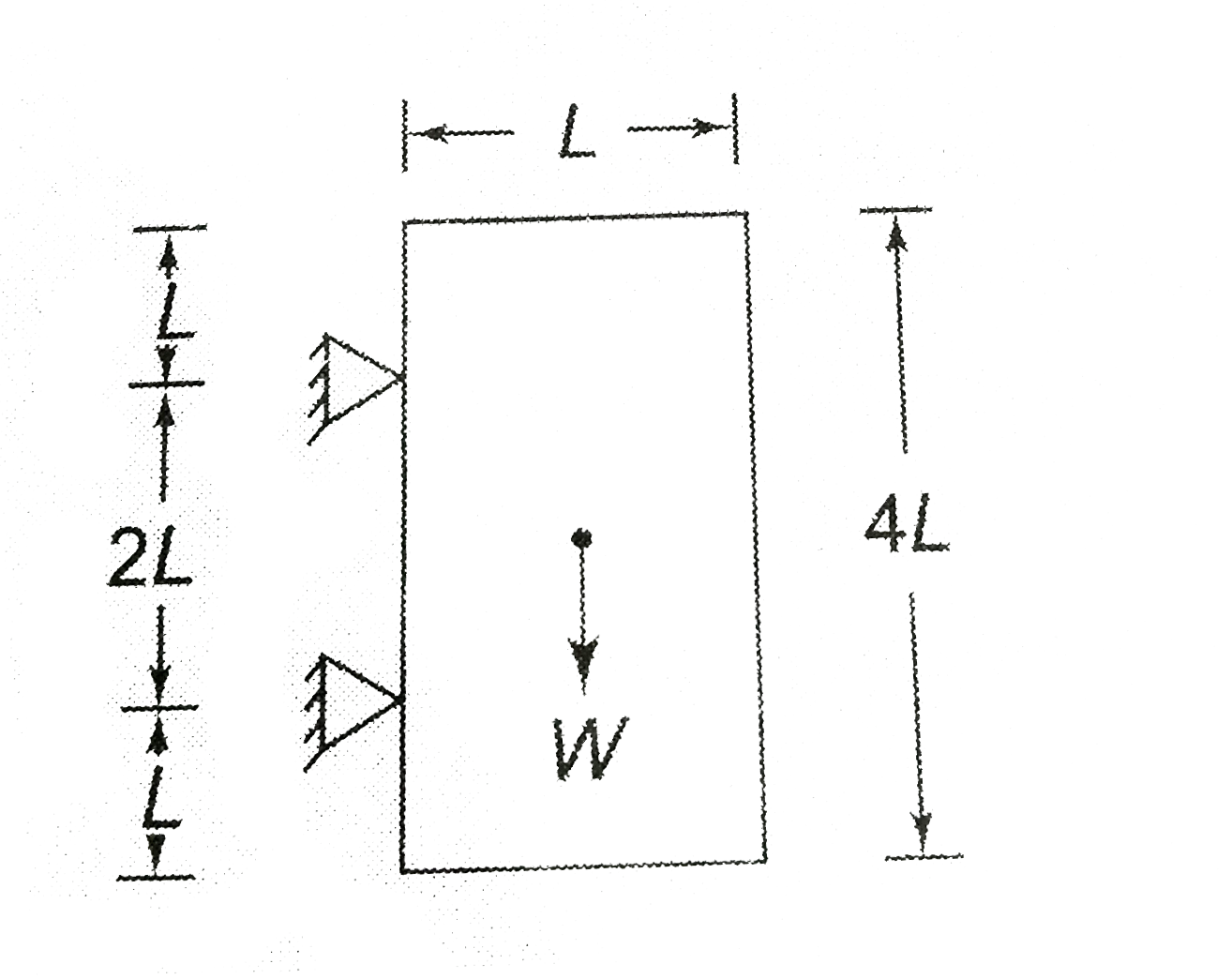
View SolutionA cubical box rests on a rough, horizontal, rectangular plank of friction coefficient `(1)/(sqrt3)`. Now the plank is slowly raised so that it makes some angle with horizontal. Find whether the box will slide first or topple.
View SolutionIn the previous problem, if the coefficient of friction is `mu`, find whether the box will slide first or topple.
(a) If the box is of height `h` having square base measuring `axxa`.
(b) If the box is hollow cylinder of radius `r` and height `h`.
View SolutionA cubical block of side a and of mass `m` rests on a rough horizontal surface. A horizontal force `F` is applied to normal to one of the faces at height `h` above the base `hgta//2`. What is the minimum value of `F` for which the cube begins to tip about an edge?
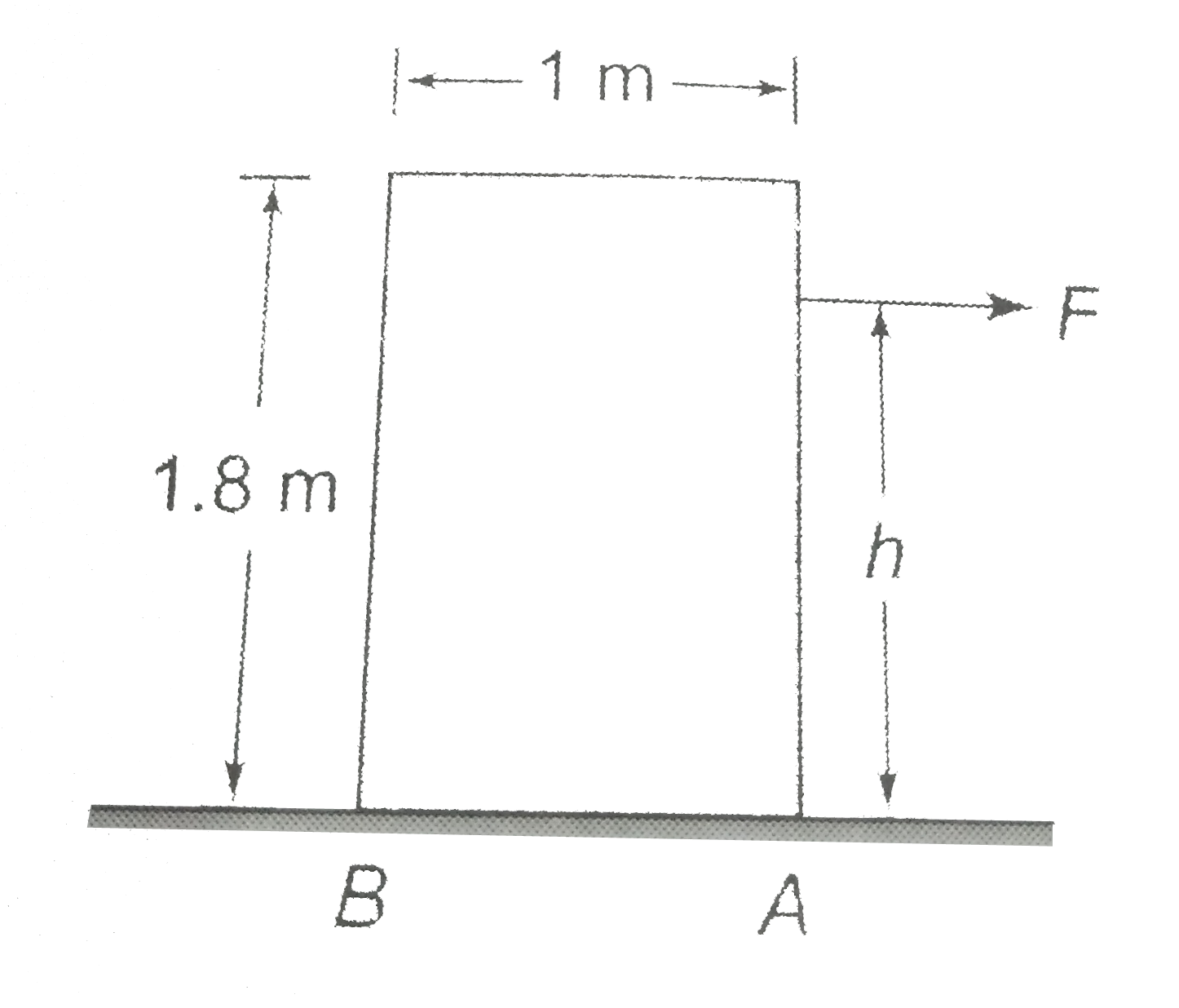
View SolutionA rectangular block of square base (`1 mxx1 m`) and height `1.8 m` is moving with constant speed on a rough horizontal surface (`mu_(k)=0.5`) due to horizontal force `F` as shown. If the mass of block is `40 kg`, find
(a) the value of `F_(1)`
(b) the value of `h` at which the block just starts to tip
(c) If force `F` is applied at `h//2`, find the perpendicular distance of normal reaction from `O` (center of mass).
View SolutionConsider a vehicle taking turn on the horizontal curve with speed `v`. If the distance between wheels is `2m`, height of center of mass above road is `1 m` and radius of circle is `57.6 m`, find the maximum value of `v` for no overturning.
View SolutionA frictionless pulley has the shape of a uniform solid disc of mass `M` and radius `R`. A stone of mass `m` is attached to a light wire that is wrapped around the rim of the pulley and a system is released from rest. If a stone falls by a distance `h`, what is the angular speed of pulley at that moment?

View SolutionConsider the situation as shown in the figure. If `m_(1)gtm_(2)`, I is the moment of intertia about its axis of rotation, `R` is the radius of pulley. The objects are released from rest separated by a vertical distance `2 h`. Find the translational speed of the objects as they pass each other. Assume no slipping.
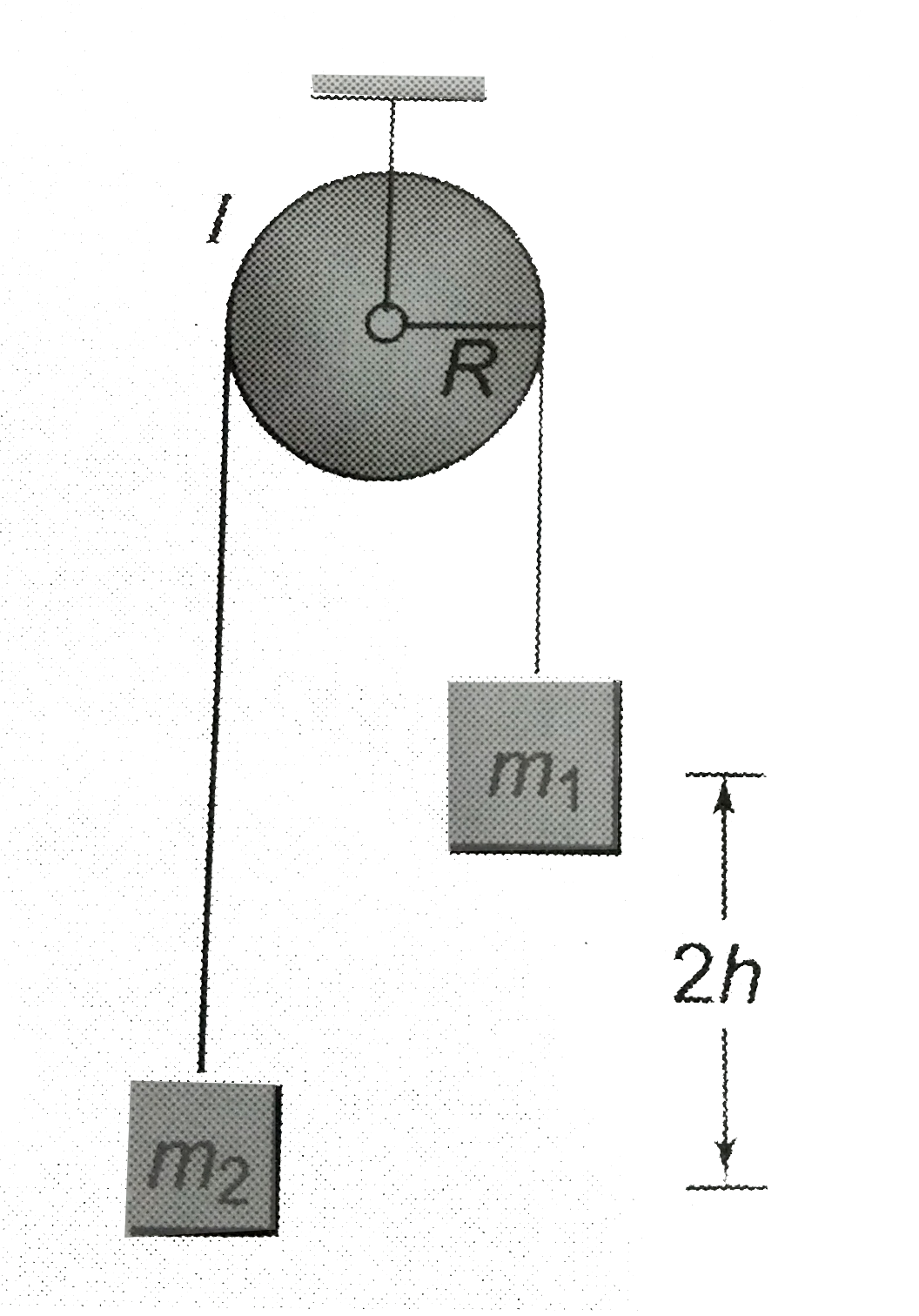
View SolutionConsider the situation as shown in the diagram. The pulley has radius `R` and moment of inertia `I`. The block is release when the spring (spring constant `k`) is unstretched. Find the speed of block when the vlock has fallen a distance `h`. Assume no slipping.

View SolutionTwo metal discs, one with radius `r` and mass `m` and the other with radius `2r` and mass `2m`, are welded together and mounted on a frictionless axis through their common center.
(a) What is the total moment of inertia of the two discs?
(b) A light string is wrapped around the edge of the smaller disc and a block of mass `m_(0)` is suspended from the free end of the string. If the block is released from rest at a distance `h`, what is its speed just before it strikes the floor?

View SolutionA uniform circular disc has radius `R` and mass `m`. A particle also of mass `m` is fixed at a point `A` on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord `PQ` that is at a distance `R//4` from the centre `C` of the disc. The line `AC` is perpendicular to `PQ`. Initially the disc is held vertical with the point `A` at its highest position. It is then allowed to fall so that it tarts rotating about `PQ`. Find the linear speed of the particle at it reaches its lowest position.
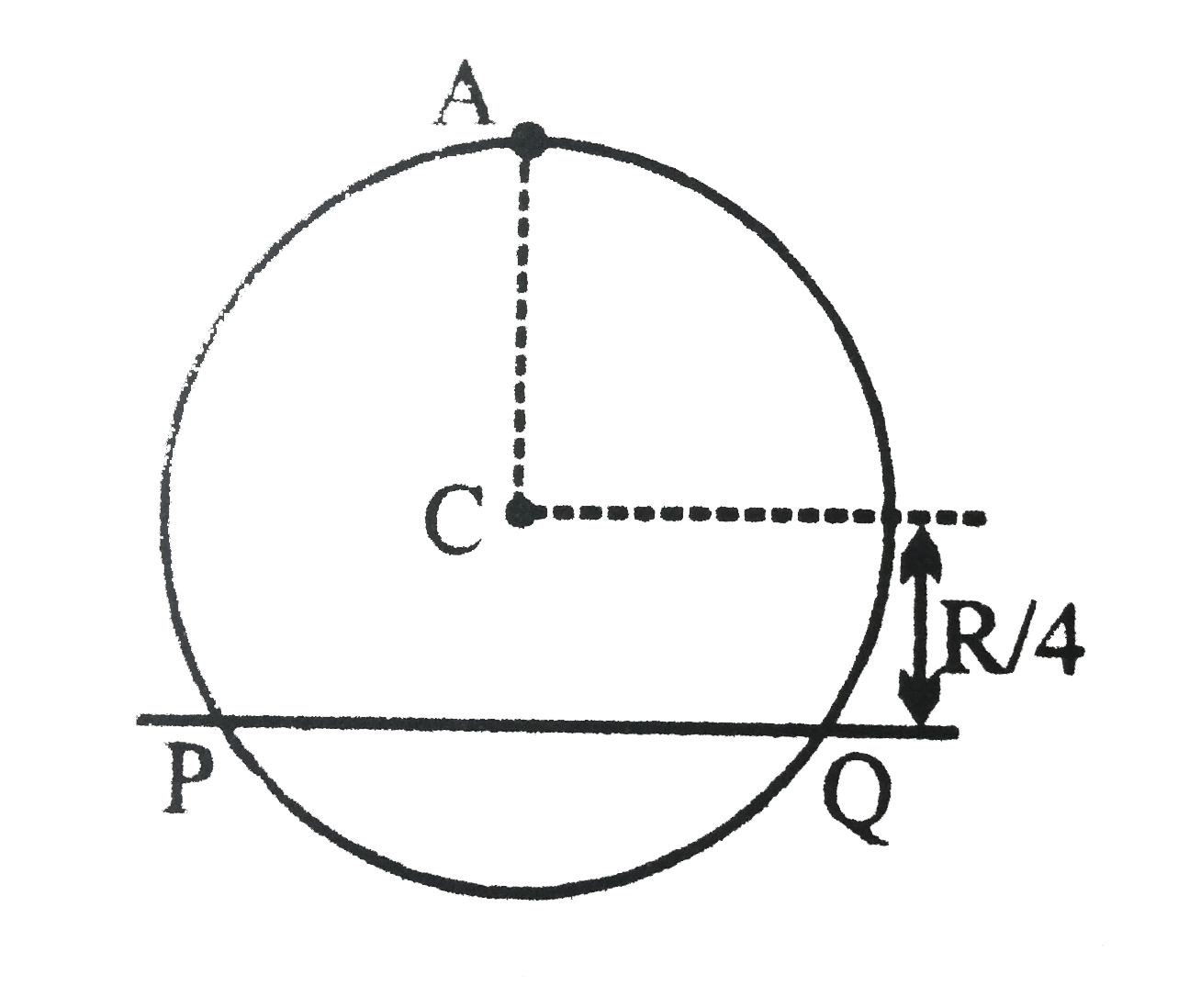 .
.
View SolutionConsider a uniform rod of mass `M` and length `L` is hinged at one end as shown. Initially the rod is vertical, it is slightly pushed and released. Find the angular velocity of rod and liner velocity of its one end when the rod becomes horizontal. Also calculate angular velocity of rod when it has rotated by an angle `theta`(`thetalt90^(@)`).
View SolutionA uniform rod of mass `M` and length `L` is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA light thread with a body of mass `m` tied to its end is wound on a uniform solid cylinder of mass `M` and radius `R`. At a moment `t=0` the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( `M=2m`).

View SolutionA block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination `30^@` to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s `10 rad s^(-1)` calculate the distance travelled by X from that instant of time until it comes to rest
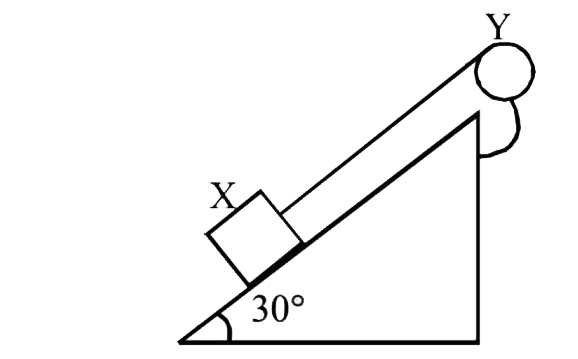
View SolutionA playground merry-go-round has radius `2 m` and moment of inertia `2000 kg m^(2)` about a vertical axle through its center.
(a) A boy applies `50 N` force tangentially to the edge of the merry-go-round for `20 s`. If the merry-go-round is initially at rest, what is its angular speed after `20 s`?
(b) How much work did the boy do on the merry-go-round?
(c) What is the average power supplied by the child?
(d) What is the instantaneous power supplied by the child at `t=20 s`?
View SolutionA flywheel of moment of inertia `10kg m^(2)` is rotating at `50 rad//s`. It must be brought to stop in `10 s`.
(a) How much work must be done to stop it?
(b) What is the required average power?
View SolutionThe engine delivers `150 kW` at an angular speed of `600 rev//min`.
(a) How much torque does the engine provide? How much work does the engine do in two revolutions?
View SolutionConsider the situation as shown in the figure. The pulley has moment of inertia `I` and radius `r`. The table is rough and the coefficient of kinetic friction is `mu_(k)`. The system is released from the rest. Calculated speed of block of mass `3m` as a function of the distance `h` it has descended. Assume no slipping.

View SolutionFind the angular momentum of the particle about `O` in the following situations.
(`a`) A particle of mass `m` moving with velocity `v` parallel to the x-axis at distance `d` from it.
(`b`) A particle of mass `m` moving with velocity `v` on a line `y=x+3`.
View SolutionA particle of mass `m` is thrown with speed `v_(0)` at angle `30^(@)` with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View SolutionTwo balls of masses `m` and `2m` are attached to the ends of a light rod of length `L`. The rod rotates with an angular speed `omega` about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionFind the angular momentum about the axis of rotation and kinetic energy.
(a) A uniform circular disc of mass `m` and radius `R` rotating about its diameter with an angular speed `omega`.
(b) A uniform square plate of mass `m` and edge `L` rotating about its diagonal with an angular speed `omega`.
View SolutionFind the angular momentum of the earth
(a) about the sun due to its orbital motion and
(b) about its axis due to its spinning motion.
View SolutionA particle of mass `m` is projected at `t=0` from the point `P` on the ground with speed `v_(0)` at an angle of `theta` to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time `t=(v_(0)sintheta)/(2g)`.
View SolutionTwo blocks of masses `2m` and `m` are connected by a light string going over a pulley of mass `2m` and radius `R` as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass `2m` has descended through a height `h`. Assume no slipping.

View SolutionIf radius of the earth is doubled without change in its mass, what will be the length of the day?
View SolutionA thin uniform circular disc of mass `M` and radius `R` is rotating in a horizontal plane about an axis passing through its center and perpendicular to its plane with an angular velocity `omega`. Now two particles each of mass `m` are placed on its perimeter along a diameter along a diameter. Find the new angular velocity. If `m=M//2`, find the percentage change in the angular velocity.
View SolutionA child stands at the turn table center of a turnable with his two arms outstretched. The turnable is set rotating with an angular speed of `10 rad//s`. If the child folds his hands back so that the moment of inertia reduces to `3//5` times the initial value, find the new angular speed. Why does the kinetic energy of child increase?
View SolutionTwo discs of moments of inertia `I_(1) and I_(2)` about their respective axes (normal to the disc and passing through the centre) and rotating with angular speeds `omega_(1) and omega_(2)` are brought into contact face to face with their axes of rotation coincident.
(a) Does the law of conservation of angular momentum apply to the situation ? Why ?
(b) Find the angular speed of the two-disc system.
(c ) Calculate the loss in kinetic energy of the system in the process.
(d) Account for this loss.
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity `omega_0` about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity `omega` in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of `90^@`, determine V.
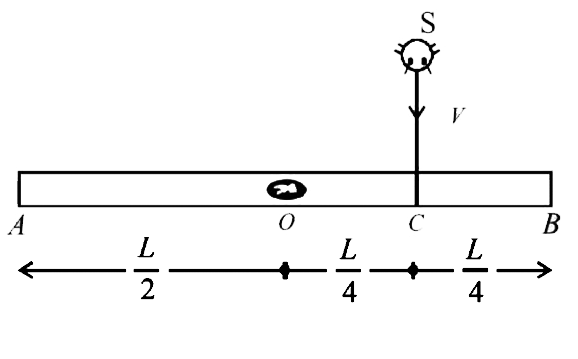
View SolutionA small block of mass `m` on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius `r` with speed `v` and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to `r//2`. (a) Find the tension in the string when the block moves in a circle of radius `r//2`. (b) Calculate the change in the kinetic energy of the block.

View SolutionA stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by `T = Ar^n` where A is a constant, r is the instantaneous radius of the circle and n=....
View SolutionA bird of mass `m` is flying horizontally with speed `v_(0)` suddenly strikes a vertical rod of mass `3m` and length `L` hinged at its base at distance `L//3` from the top of the rod. After collision the bird drops to the ground (but soon recovers to fly happly away). What is the angular velocity of the rod
(a) just after it is hit by the bird and
(b) just as it reaches the ground?
View SolutionA wooden log of mass `M` and length `L` is hinged by a frictionless nail at `O`. A bullet of mass `m` strikes with velocity `v` and sticks to it. Find the angular velocity of the system, immediately after the collision about `O`. Also, calculate the minimum value of `v` so that log becomes horizontal after collision.
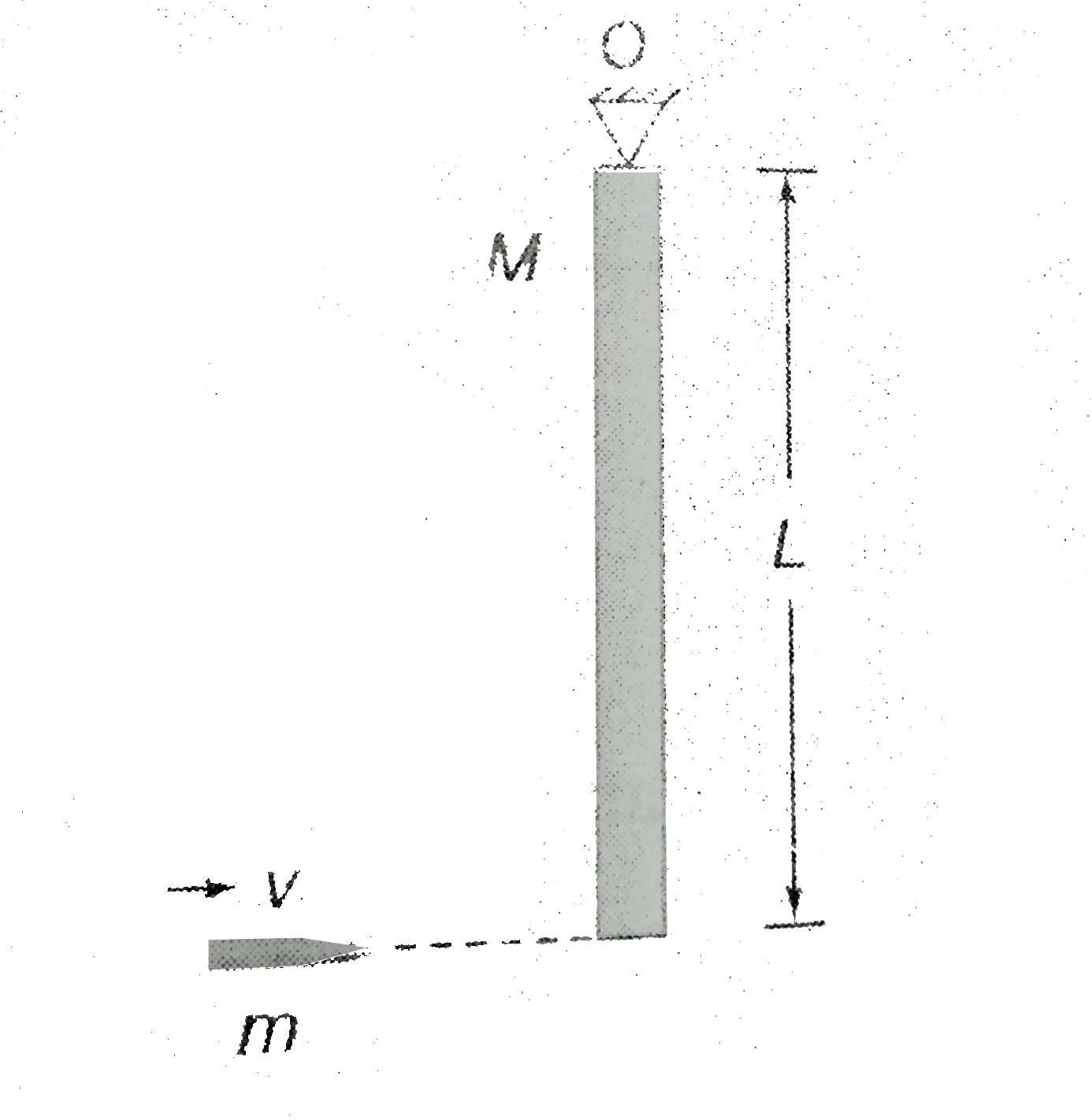
View Solution
Example questions and complete solutions for chapter ROTATIONAL MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11