Complete Solutions to Level 1 Subjective of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
A particle of mass `1 kg` is kept on the surface of a uniform sphere of mass `20 kg` and radius `1.0 m`. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionWhat is the fractional decrease in the value of free-fall acceleration g for a particle when it is lifted from the surface to an elevation `h`? `(h lt lt R)`
View SolutionTwo masses `m_(1)` and `m_(2)` at an infinite distance from each other are initially at rest, start interacting gravitationally. Find their velocity of approach when they are at a distance `r` apart.
View SolutionIf a satellites is revolving close to a planet of density `rho` with period `T`, show that the quantity `rho T_(2)` is a universal constant.
View SolutionA satellite is revolving around a planet in a circular orbit. What will happen, if its speed is increased from `upsilon_(0)` to
(a) `sqrt(1.5) upsilon_(0)` (b) `2 upsilon_(0)`
View SolutionIf the radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionTwo concentric spherical shells have masses `m_(1)`, `m_(2)` and radit `R_(1)`,`R_(2) (R_(1) lt R_(2))`. Calculate the force by this system on a particle of mass `m`, if it is placed at a distance `((R_(1) + R_(2)))/(2)` from the centre.
View SolutionA semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
View SolutionA rocket is accelerated to speed `upsilon = 2sqrt(gR)` near the earth's surface (`R =` radius of earth). Show that very far from earth its speed will be `upsilon = sqrt(2gR)`.
View SolutionTwo spheres one of mass `M` has radius `R`. Another sphere has mass `4M` and radius `2R`. The centre to centre distance between them is `12 R`. Find the distance from the centre of smaller sphere where
(a) net gravitational field is zero,
(b) net gravitational potential is half the potential on the surface of larger sphere.
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a. Find the gravitational field at a distance a). 3/2 a from the centre , b). 5/2 as from the centre.
View SolutionThe density inside a solid sphere of radius a is given by `rho=rho_0/r`, where `rho_0` is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionTwo neutron stars are separated by a distance of `10^(10) m`. They each have a mass of `10^(30) kg` and a radius of `10^(5) m`. They are initially at rest with respect to each other.
As measured from the rest frame, how fast are they moving when
(a) their separation has decreaed to one - half its initial value,
(b) they are about to collide .
View SolutionA mass `m` is taken to a height `R` from the surface of the earth and then is given a vertical velocity `upsilon`. Find the minimum value of `upsilon`, so that mass never returns to the surface of the earth. (Radius of earth is `R` and mass of the earth `m`).
View SolutionIn the figure masses `400 kg` and `100 kg` are fixed.
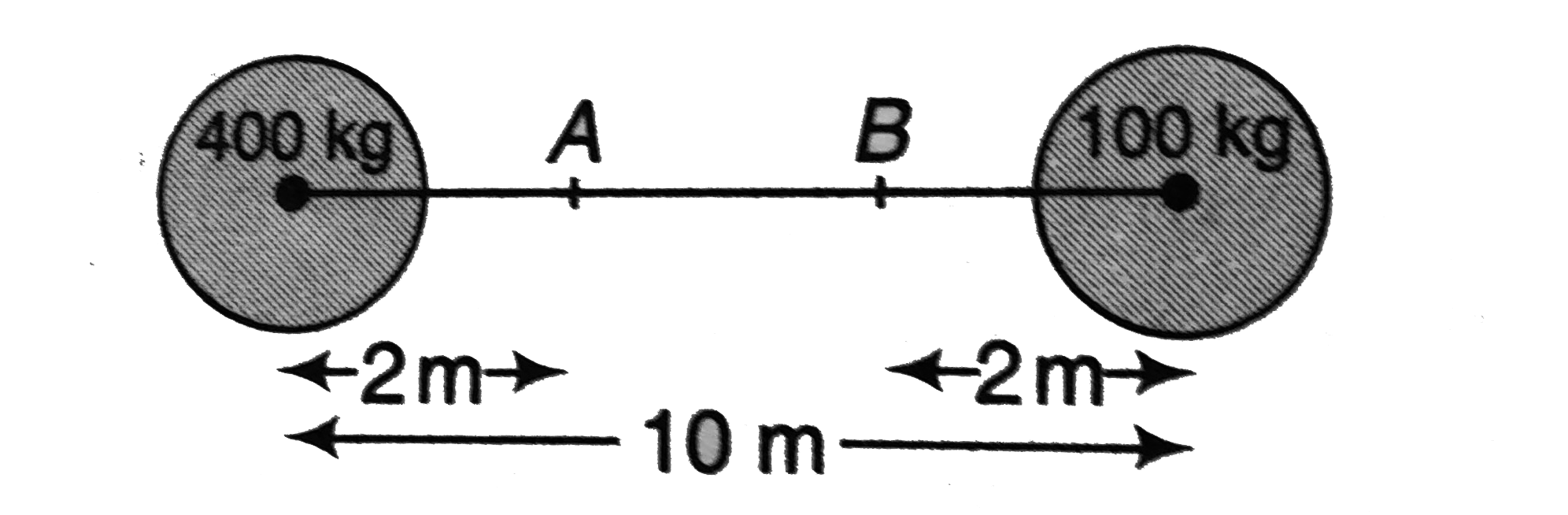
(a) How much work must be done to move a `1 kg` mass from point `A` to point `B`?
(b) What is the minimum kinetic energy with which the `1 kg` mass must be projected from `A` to the right to reach the point `B`?
View SolutionTwo identical stars of mass `M` orbit around their centre of mass. Each orbit is circular and has radius `R`, so that the two stars are always on opposite of the circle.
(a) Find the gravitational force of one star on the other.
(b) Find the orbital speed of each star and the period of the orbit.
(c ) What minimum energy would be required to separate the two stars to infinity?
View SolutionConsider two satellites `A` and `B` of equal mass, moving in the same circular orbit of radius `r` around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy `E_(A) + E_(B)` of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View Solution(a) Does it take more energy to get a satellite upto `1500 km` above earth than to put in circular orbit once it is there.
(b) What about `3185 km` ?
(c ) What about `4500 km`? (Take `R_(e) = 6370 km`)
View Solution
Level 1 Subjective questions and complete solutions for chapter GRAVITATION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples