Complete Solutions to Level 2 Subjective of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY | Level 2 Subjective |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionA man can jump vertically to a height of `1.5 m` on the earth. Calculate the radius of a planet of the same mean density as that of the earth from whose gravitational field he could escape by jumping. Radius of earth is `6.41 xx 10^(5) m`.
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
View SolutionA uniform metal sphere of radius `R` and mass `m` is surrounded by a thin uniform spherical shell of same mass and radius `4R`. The centre of the shell `C` falls on the surface of the inner sphere. Find the gravitational fields at points `A` and `B`.

View SolutionFigure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was `M`. With what gravitational force does the hollowed out lead sphere attract a particle of mass `m` that lies at a distance `d` from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
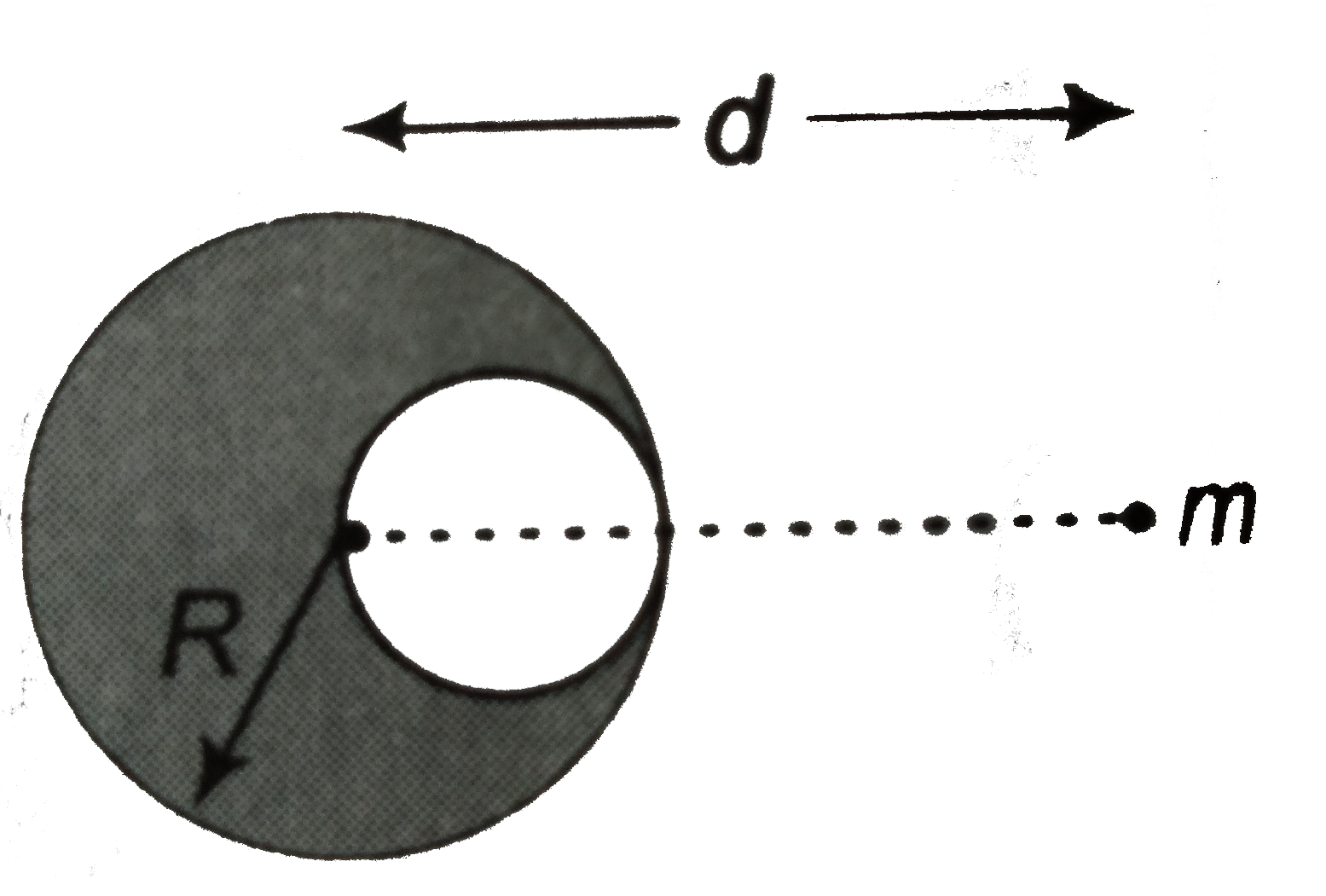
View SolutionThe density of the core a planet is `rho_(1)` and that of the outer shell is `rho_(2)`. The radii of the core and that of the planet are `R` and `2R` respectively. The acceleration due to gravity at the surface of the planet is same as at a depth `R`. Find the radio of `(rho_(1))/(rho_(2))`

View SolutionIf a satellite is revolving around a plenet of mass `M` in an elliptical orbit of semi-major axis `a`. Show that the orbital speed of the satellite when it is a distance `r` from the focus will be given by
`upsilon^(2) = GM[(2)/(r ) - (1)/(a)]`
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance `sqrt3` a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionDistance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` and their radii `a` and `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of `G`, `M` and `a`.
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is `0.5`. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is `M` and radius of the earth is `R`.
View SolutionInside a fixed sphere of radius `R` and uniform density `rho`, there is spherical cavity of radius `(R )/(2)` such that surface of the cavity passes through the centre of the sphere as shows in figure. A particle of mass `m_(0)` is released from rest at centre `B` of the cavity. Caculate velocity with which particle strikes the centre `A` of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.

View SolutionA ring of radius `R = 4m` is made of a highly dense material. Mass of the ring is `m_(1) = 5.4 xx 10^(9) kg` distributed uniformly over its circumference. A highly dense particle of mass `m_(2) = 6 xx 10^(8) kg` is placed on the axis of the ring at a distance `x_(0) = 3 m` from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionTwo planets of equal mass orbit a much massive star (figure). Planet `m_(1)` moves in circular orbit of radius `1 xx 10^(8) km` with period `2 yr`. Planet `m_(2)` moves in an elliptical orbit with closed distance `r_(1) = 1 xx 10^(8) km` and farthest distance `r_(2) = 1.8 xx 10^(8) km`, as shows.
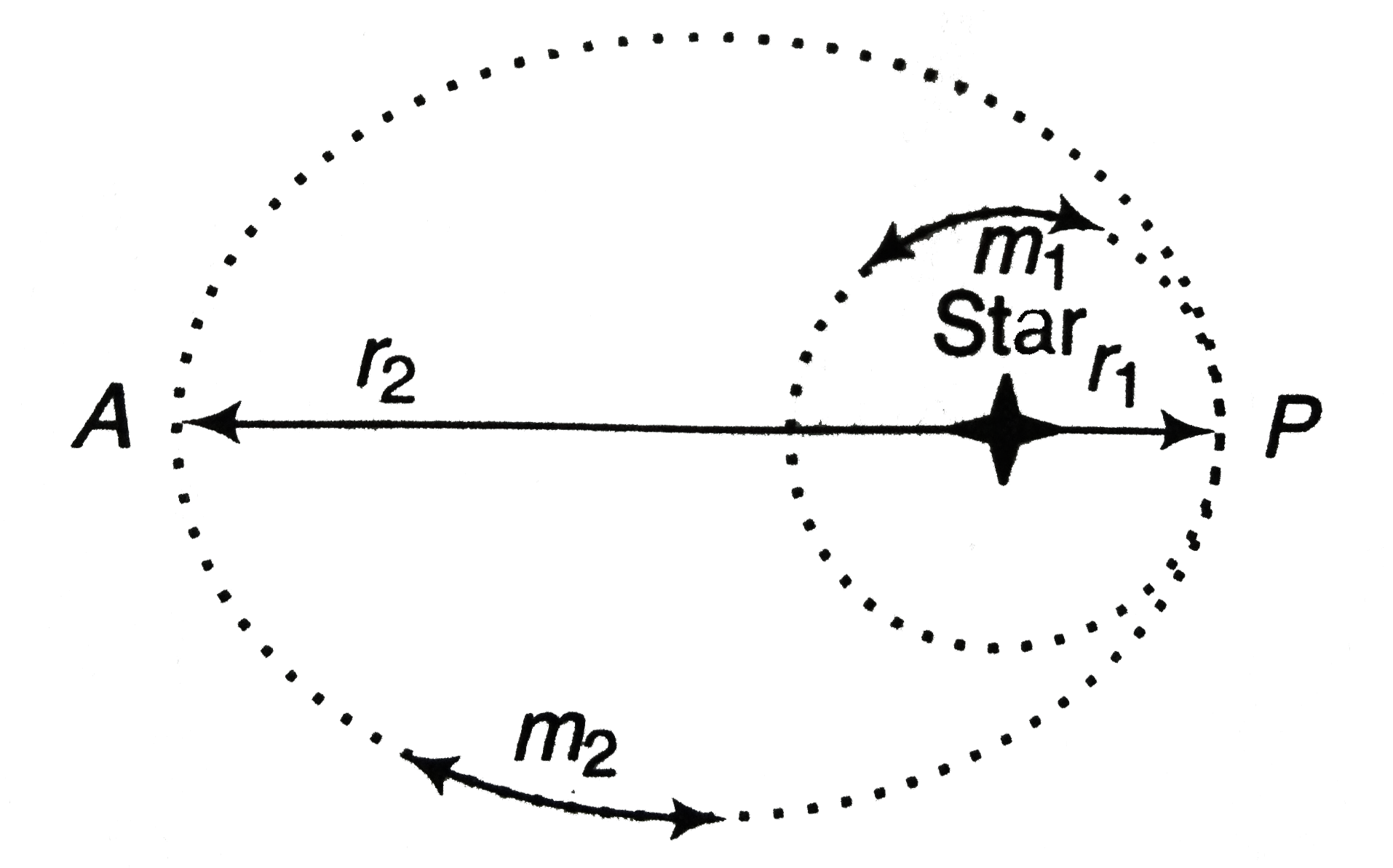
(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of `m_(2)'s` orbit.
(b) Which planet has the greater speed at point `P`? Which has the greater total energy?
(c ) Compare the speed of planet `m_(2)` at `P` with that at `A`.
View SolutionIn a double star, two stars one of mass `m_(1)` and another of mass `m_(2)`, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View Solution
Level 2 Subjective questions and complete solutions for chapter GRAVITATION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples