Complete Solutions to (C) Chapter Exercises of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY NEET | (C) Chapter Exercises |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
Starting from the centre of the earth having radius R, the variation of `g` (acceleration due to gravity) is shown by
View SolutionA satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of `g_(0)`, the value of acceleration due to gravity at the earth's surface is
View SolutionAt what height from the surface of earth the gravitation potential and the value of `g` are `- 5.4 xx 10^(7) J kg^(-2)` and `6.0 ms^(-2)` respectively ? Take the radius of earth as `6400 km`:
View SolutionThe ratio of escape velocity at earth `(V_(e))` to the escape velocity at a planet `(V_(p))` whose radius and mean density are twice as that of earth is
View SolutionKepler's third law states that square of period of revolution (T) of a planet around the sun, is proportional to third power of average distace r between the sun and planet i.e. `T^(2) = Kr^(3)`, here K is constant. If the masses of the sun and planet are M and m respectively, then as per Newton's law of gravitationa force of attraction between them is `F = (GMm)/(r^(2))`, hence G is gravitational constant. The relation between G and K is described as
View SolutionThe reading of a spring balance corresponds to 100 N while situated at the north pole and a body is kept on it. The weight record on the same scale if it is shifted to the equator, is (take, `g = 19 " ms"^(2-)` and radius of the earth, `R = 6.4 xx 10^(6)` m)
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionWhat would be the value of acceleration due to gravity at a point 5 km below the earth's surface ? `(R_(E) = 6400 km, g_(E) = 9.8 "ms"^(-2))`
View SolutionTwo particles of equal mass `m` go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
View SolutionWhat would be the escape velocity from the moon, it the mass of the moon is `7.4 xx 10^(22)` kg and its radius is 1740 km ?
View SolutionTwo spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
View SolutionOrbital velocity of an artificial satellite does not depend upon
View SolutionGravitational potential energy of body of mass `m` at a height of `h` above the surface of earth (M = mass of earth , R = radius of earth) is
View SolutionAccording to Kepler's law of planetary motion, if T represents time period and `r` is orbital radius, then for two planets these are related as
View SolutionIf mass of a body is `M` on the earth surface, then the mass of the same body on the moon surface is
View SolutionTwo spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
View SolutionThe force of gravitation is
View SolutionDependence of intensity of gravitational field `(E)` of earth with distance `(r)` from centre of earth is correctly represented by
View SolutionKeeping the mass of the earth as constant, if its radius is reduced to 1/4th of its initial value, then the period of revolution of the earth about its own axis and passing through the centre, (in hours) is (assume the earth to be a solid sphere and its initial period of rotation as 24 h)
View SolutionA body of mass `m` is raised to a height 10 R from the surface of the earth, where R is the radius of the earth. Find the increase in potential energy. (G = universal constant of gravitational, M = mass of the earth and g= acceleration due to gravity)
View SolutionAn artificial satellite moving in a circular orbit around the earth has a total energy `E_(0)`. Its potential energy is
View SolutionWhat is a period of revolution of the earth satellite ? Ignore the height of satellite above the surface of the earth.
Given,
(i) the value of gravitational acceleration, `g = 10 ms^(-2)`
(ii) radius of the earth, `R_(g) =6400` km (take, `pi = 3.14`)
View SolutionThe time period of the earth's satellite revolving at a height of 35800 km is
View SolutionAt a height H from the surface of earth, the total energy of a satellite is equal to the potential energy of a body of equal mass at a height 3R from the surface of the earth (R = radius of the earth). The value of H is
View SolutionA body of mass `m` taken form the earth's surface to the height is equal to twice the radius `(R)` of the earth. The change in potential energy of body will be
View SolutionInfinite number of bodies, each of mass `2kg`, are situated on `x`-axis at distance `1m,2m,4m,8m.........` respectively, from the origin. The resulting gravitational potential the to this system at the origing will be
View SolutionThe universal law of gravitational is the force law known also as the
View SolutionThe value of acceleration due to gravity at the surface of earth
View SolutionThe escape velocity of a particle of a particle from the surface of the earth is given by
View SolutionIf earth were to rotate on its own axis such that the weight of a person at the equator becomes half the weight at the poles, then its time period of rotation is (g = acceleration due to gravity near the poles and R is the radius of earth) (Ignore equatorial bulge)
View SolutionThe earth moves around the Sun in an elliptical orbit as shown figure. The ratio OA/OB=x. The ratio of the speed of the earth at B to that at A is nearly
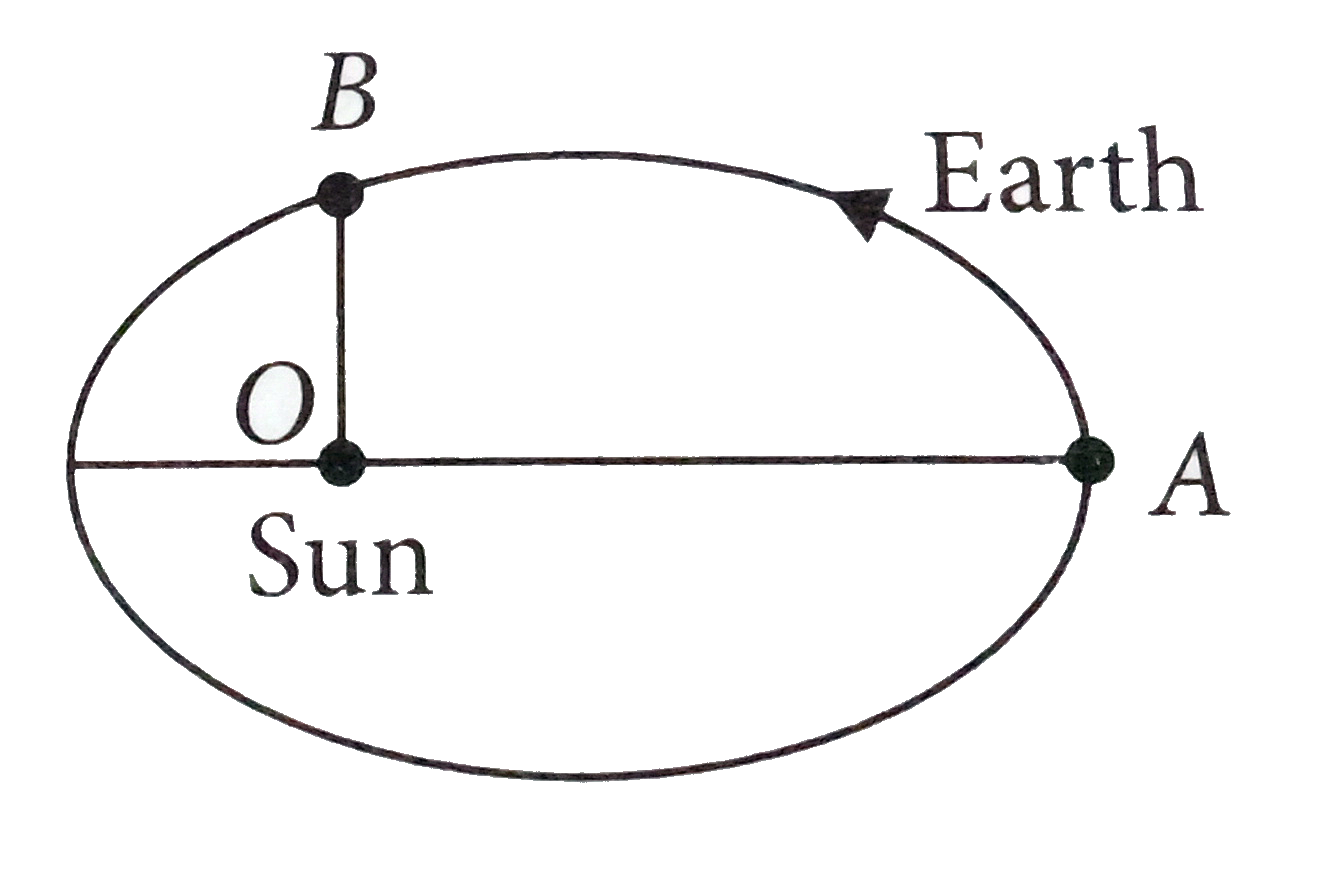
View SolutionThe radii of two planets are respectively `R_1 and R_2` and their densities are respectively `rho_1 and rho_2`. The ratio of the accelerations due to gravity `(g_1//g_2)` at their surfaces is
View SolutionThe weight of an object is 90 kg at the surface of the earth. If it is taken to a height equal to half of the radius of the earth, then its weight will become
View SolutionThe escape velocity from earth is `v_(e)`. A body is projected with velocity `2v_(e)`. With what constant velocity will it move in the inter planetary space ?
View SolutionA satellite of mass `m` is circulating around the earth with constant angular velocity. If the radius is `R_(0)` and mass of earth is M, then the angular momentum about the centre of the earth is
View SolutionTwo identical thin ring each of radius `R` are co-axially placed at a distance `R`. If the ring have a uniform mass distribution and each has mass `m_(1)` and `m_(2)` respectively, then the work done in moving a mass `m` from the centre of one ring to that of the other is :
View SolutionIf r is the distance between the Earth and the Sun. Then, angular momentum of the Earth around the sun is proportional to
View SolutionA spherical planet far out in space has a mass `M_(0)` and diameter `D_(0)`. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
View SolutionA geostationary satellite is orbiting the earth at a height of `5R` above the surface of the earth, `2R` being the radius of the earth. The time period of another satellite in hours at a height of `2R` form the surface of the earth is
View SolutionWhen a satellite is moving around the earth with velocity `v`, then to make the satellite escape, the minimum percentage increase in its velocity should be
View SolutionA lauching vehicle carrying an artificial satellite of mass `m` is set for launch on the surface of the earth of mass `M` and radius `R`. If the satellite intended to move in a circular orbit of radius `7R`, the minimum energy required to be spent by the launching vehicle on the satellite is
View SolutionConsider a satellite orbiting the earth as shown in the figure below. Let `L_(a) and L_(p)` represent the angular momentum of the satellite about the earth when at aphelion and perihelion respectively. Consider the following relations

(i) `L_(a)=L_(p)`
(ii) `L_(a)=-L_(p)`
(iii) `r_(a)xxL_(a) =r_(p)xxL_(p)`
Which of the above relation(s) is/are true ?
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is
View SolutionFind the imaginary angular velocity of the earth for which the effective acceleration due to gravity at the equator shall be zero. (take `g = 10 m//s^(2)` for the acceleration due to gravity, if the earth were at rest and radius of earth equal to 6400 km and `phi = 60^(@)`)
View SolutionThe mass of the moon is (1/8) of the earth but the gravitational pull is (1/6) of the earth. It is due to the fact that
View Solution
(C) Chapter Exercises questions and complete solutions for chapter GRAVITATION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY NEET Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples