Complete Solutions to (A) Chapter Exercises of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DC PANDEY NEET | (A) Chapter Exercises |
| Number Of Questions | 68 |
| Academic Year | 2023-24 |
Weightlessness in satellite is due to
View SolutionThe value of acceleration due to gravity at the surface of earth
View SolutionA satellite of the earth is revolving in a circular orbit with a uniform speed `v`. If gravitational force suddenly disappears, the satellite will
View SolutionThe weight of an object in the coal mine, sea level and at the top of the mountain are `W_(1),W_(2)` and `W_(3)` respectively, then
View SolutionA body is projected from earth's surface to become its satellite, its time period of revolution will not depend upon
View SolutionIf orbit velocity of planet is given by `v = G^(a)M^(b)R^(c)`, then
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet of mass m is in an elliptical orbit about the sun (m << `M_"sun"`) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View SolutionTo required kinetic energy of an object of mass `m`, so that it may escape, will be
View SolutionWhat is the fractional decrease in the value of free-fall acceleration g for a particle when it is lifted from the surface to an elevation `h`? `(h lt lt R)`
View SolutionThe earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity.
View SolutionAs observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed form earth , this would
View SolutionSatellite orbiting the earth have finite life and sometimes debris of satellite fall to the earth. This is because,
View SolutionBoth earth and moon are subjected to the gravitational force of the sun. As observed from the sun, the orbit of the moon
View SolutionIn our solar system, the inter-planetary region has chunks of matter ( much smaller in size compared to planets) called asteroids. They
View SolutionChoose the wrong option
View SolutionDifferent points in the earth are at slightly different distances from the sun and hence experience different forces due to gravitation.
For a rigid body, we know that if various forces act at various points in it, the resulant motion is as if net force acts on the CM (centre of mass) causing translation and a net torque at the CM causing rotation around an axis through the CM. For the earth-sun system (approximating the earth as a uniform density sphere)
View SolutionTwo satellite of same mass are launched in the same orbit of radius `r` around the earth so as to rotate opposite to each other. If they collide inelastically and stick together as wreckage, the total energy of the system just after collision is
View SolutionCompute the additional velocity required by a satellite orbiting around earth with radius 2R to become free from earth's gravitational field. Mass of earth is M.
View SolutionParticles of masses 2M, m and M are respectively at points A, B and C with `sqrt((GM)/(R))(sqrt(2)+1)` is much-much smaller than M and at time `t=0`, they are all at rest as given in figure
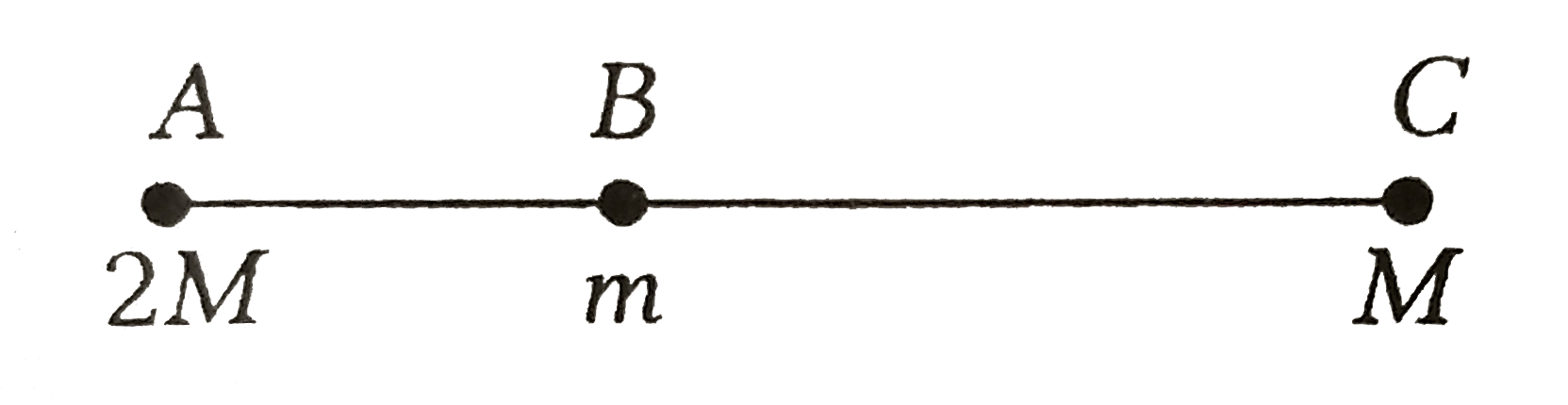
At subsequent time before any collision takes place.
View SolutionEarth orbiting satellite will escape if
View SolutionThe energy required to move a satellite of mass m from an orbit of radius 2R to 3R is (where M is the mass of the earth and R is the radius of the earth)
View SolutionA body attains a height equal to the radius of the earth. The velocity of the body with which it was projected is
View SolutionSuppose the gravitational attraction varies inversely as the distance from the earth. The orbital velocity of a satellite in such a case varies as nth power of distance where `n` is equal to
View SolutionThe rotation of the earth about its axis speeds up such that a man on the equator becomes weightness. In such a situation, what would be the duration of one day ?
View SolutionThe rotation of the earth radius R about its axis speeds upto a value such that a man at latitude angle `60^(@)` feels weightless. The duration of the day in such case will be
View SolutionAssume the radius of the earth to be `6.4xx10^(6)m`
a. Calculate the time period `T` of a satellite on equational orbit at `1.4xx10^(e)m` above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?
View SolutionIf gravitational attraction between two points masses be given by `F=G(m_(1)m_(2))/(r^(n))`. Then the period of a satellite in a circular orbit will be proportional to
View SolutionSuppose the gravitational force varies inversely as the `n^(th) `power of distance. Then the time period of a planet in circular orbit of radius R around the sun will be proportional to-
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If `R` is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA particle takes a time `t_(1)` to move down a straight tunnel from the surface of earth to its centre. If gravity were to remain constant this time would be `t_(2)` calculate the ratio `(t_(1))/(t_(2))`
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View SolutionA body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity on reaching the surface of earth. Take `g=` acceleration due to gravity on the surface of the Earth.
View SolutionA planet of mass `m` moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are `r_(1)` and `r_(2)`, respectively. Find the relation between the time period of the planet in terms of `r_(1)` and `r_(2)`.
View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed `v`. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionSuppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of the earth is uniformly distributed over its volume. Then, which of the following statements are not correct?
View SolutionA satellite is moving in a circular orbit round the earth with a diameter of orbit 2R. At a certain point a rocket fixed to the satellite is fired such that it increases the velocity of the satellite tangentially. The resulting orbit of the satellite would be
View SolutionIf the mass of moon is `(M)/(81)`, where M is the mass of earth, find the distance of the point where gravitational field due to earth and moon cancel each other, from the centre of moon. Given the distance between centres of earth and moon is 60 R where R is the radius of earth
View SolutionWhat is the energy required to launch a `m` kg satellite from earth's surface in a circular orbit at an altitude of 7R ? (R = radius of the earth)
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L . If the distance is increased to 16 r, then the new angular momentum will be
View SolutionTwo spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before collision is
View SolutionTwo spheres of masses `m and 2m` are separated by distance `d`. A particle of mass `(m)/(5)` is projected straight from `2m` towards `m` with a velocity `v_(0)`. Which of the following statements is correct ?
View SolutionA ring of mass `m_(1)` and radius R is fixed in space at some location. An external agent brings a point mass `m_(2)` from infinity to centre of the ring. Work done by the external agent will be
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the surface of earth. (Radius of earth `= 6400 km`)
(a) Dentermine the height of the satellite above the earth's surface.
(b) If the satellite is stopped suddenly in its orbit and allowed to fall freely on the earth, find the speed with which it hits the surface of earth.
View SolutionA person brings a mass of 1 kg from infinity to a point . Initally the mass was at rest but it moves at a speed of 2 `ms^-1` as it reaches A. The work done by the person on the mass is -3J. The potential at A is
View SolutionWhat impulse need to be given to a body of mass `m`, released from the surface of earth along a straight tunnel passing through centre of earth, at the centre of earth, to bring it to rest. (Mass of earth M, radius of earth R)

View SolutionThe figure represents two concentric shells of radii `R_(1)` and `R_(2)` and masses `M_(1)` and `M_(2)` respectively. The gravitational field intensity at the point `A` at distance `a (R_(1) lt a lt R_(2))` is

View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionEnergy of a satellite in circular orbit is `E_(0)`. The energy required to move the satellite to a circular orbit of 3 times the radius of the initial orbit is
View SolutionPertaining to two planets, the ratio of escape velocities from respectivie surfaces is 1:2 , the ratio of the time period of the same simple pendulum at their respective surface is 2:1 (in same order). Then the ratio of their average densities is 1:n. Find the value of n.
View SolutionAn object is released from a height twice the radius of the earth on the surface of earth. Find the speed with which it will collide with group by neglecting effect of air. (Take, R radius of earth and mass of earth as M)
View SolutionA planet of mass `m` revolves in elliptical orbit around the sun of mass `M` so that its maximum and minimum distance from the sun equal to `r_(a)` and `r_(p)` respectively. Find the angular momentum of this planet relative to the sun.
View SolutionThe magnitude of gravitational field at distances `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M`,are `(I_(1))` and `(I_(2))` respectively. Find the ratio of `(I_(1))//(I_(2)))` if `r_(1)gtR` and `r_(2)ltR`.
View SolutionTwo particles of mass `m` and M are initialljy at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when `d` is their separation at any instant
View SolutionThe ratio of the energy required to raise a satellite upto a height h above the earth of radius R to that the kinetic energy of the satellite into that orbit is
View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
View SolutionThe energy required to take a satellite to a height ‘h’ above Earth surface (radius of Earth`=6.4xx10^3` km ) is `E_1` and kinetic energy required for the satellite to be in a circular orbit at this height is `E_2`. The value of h for which `E_1` and `E_2` are equal, is:
View SolutionA satellite is revolving round the earth with orbital speed `v_(0)` if it is imagined to stop suddenly the speed with which it will strike the surface of the earth would be `(v_(e)` - escape speed of a body from earth s surface)
View SolutionFour particles, each of mass `M`, move along a circle of radius `R` under the acting of their mutual graviational attraction. The speed of each particle is
View SolutionThree particle each of mass `m`, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
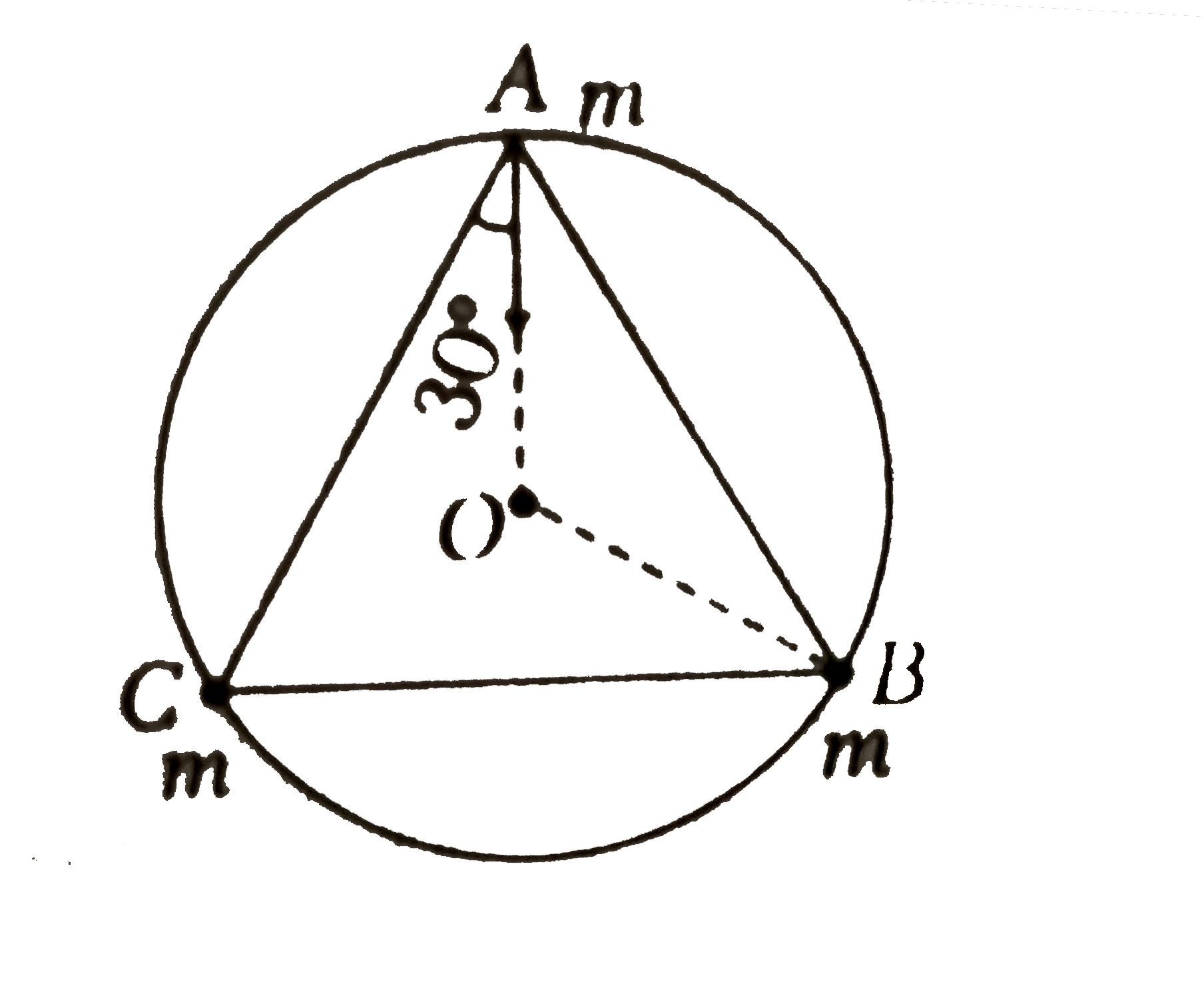
View SolutionThree point masses each of mass `m` rotate in a circle of radius `r` with constant angular velocity `omega` due to their mutual gravitational attraction. If at any instant, the masses are on the vertices of an equilateral triangle of side `a`, then the value of `omega` is
View SolutionTwo identical thin rings each of radius R are coaxially placed at a distance R. If the rings have a uniform mass distribution and each has masses `2m` and `4m` respectively, then the work done in moving a mass `m` from centre of one ring to that of the other is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass `m` is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass `m` is
View SolutionA point `P(R sqrt(3),0,0)` lies on the axis of a ring of mass M and radius R. The ring is located in yx-plane with its centre at origin O. A small particle of mass `m` starts from P and reaches O under gravitational attraction only. Its speed at O will be
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
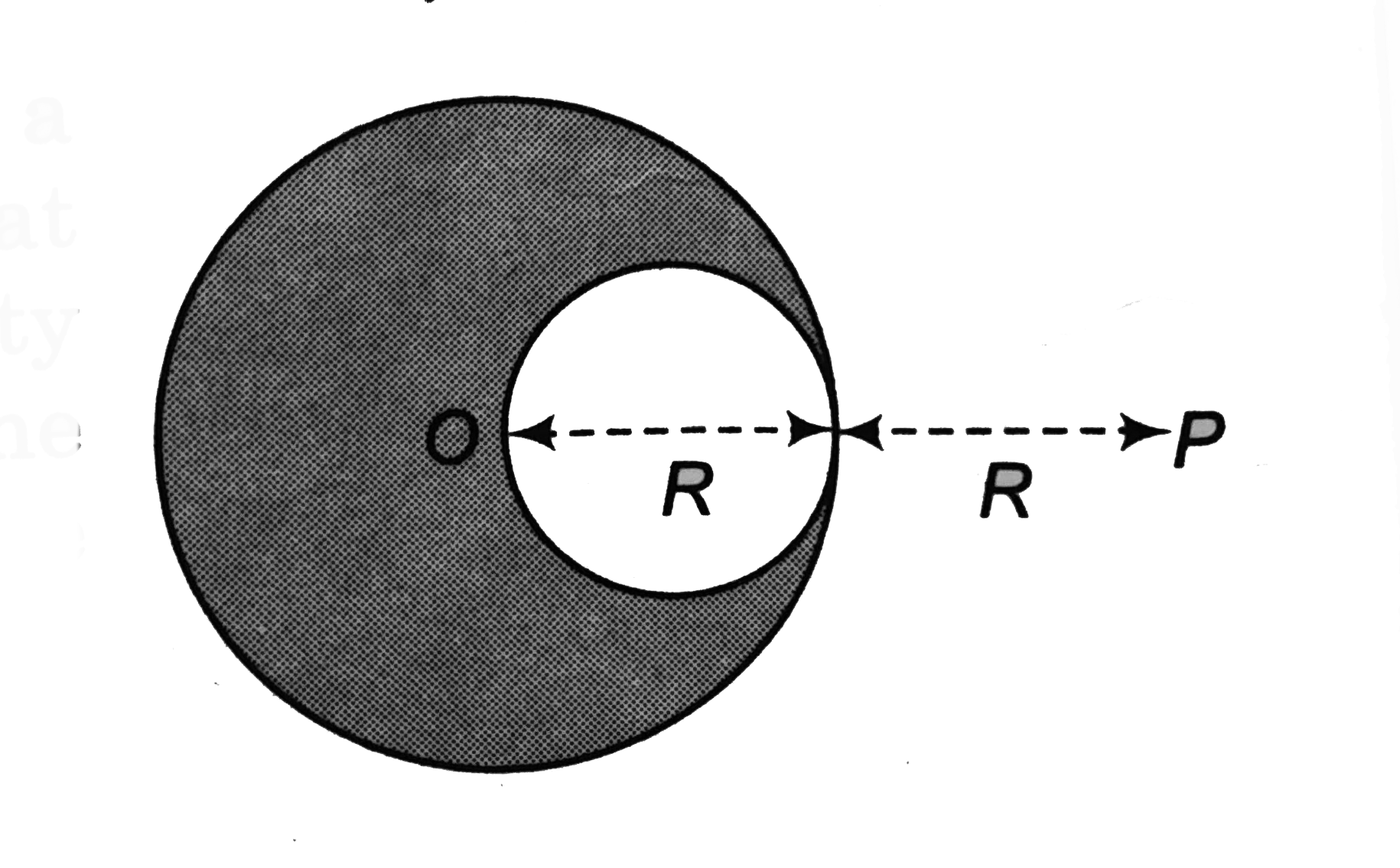
View SolutionSuppose a vertical tunnel is dug along the diameter of earth , which is assumed to be a sphere of uniform mass density `rho`. If a body of mass `m` is thrown in this tunnel, its acceleration at a distance `y` from the centre is given by

View Solution
(A) Chapter Exercises questions and complete solutions for chapter GRAVITATION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY NEET Class 11 PHYSICS GRAVITATION
- (A) Chapter Exercises
- (B) Chapter Exercises
- (C) Chapter Exercises
- Check Point 10.1
- Check Point 10.2
- Check Point 10.3
- Check Point 10.4
- Check Point 10.5
- Check Point 10.6
- Example
- Exercise 13.1
- Exercise 13.2
- Exercise 13.3
- Exercise 13.4
- Exercise 13.5
- Exercise 13.6
- Exercise 13.7
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Examples