Complete Solutions to Comprehension types of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | Comprehension types |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Passage I) In simple harmonic motion force acting on a particle is given as `F=-4x`, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is `-16m/s^(2)`. Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is
View SolutionPassage I) In simple harmonic motion force acting on a particle is given as `F=-4x`, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is `-16m/s^(2)`. Mass of the particle is 0.5 kg.
Displacement time equation equation of the particle is
View SolutionPassage I) In simple harmonic motion force acting on a particle is given as `F=-4x`, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is `-16m/s^(2)`. Mass of the particle is 0.5 kg.
At x=+1m, potential energy and kinetic energy of the particle are
View SolutionPassage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by `A/2` and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
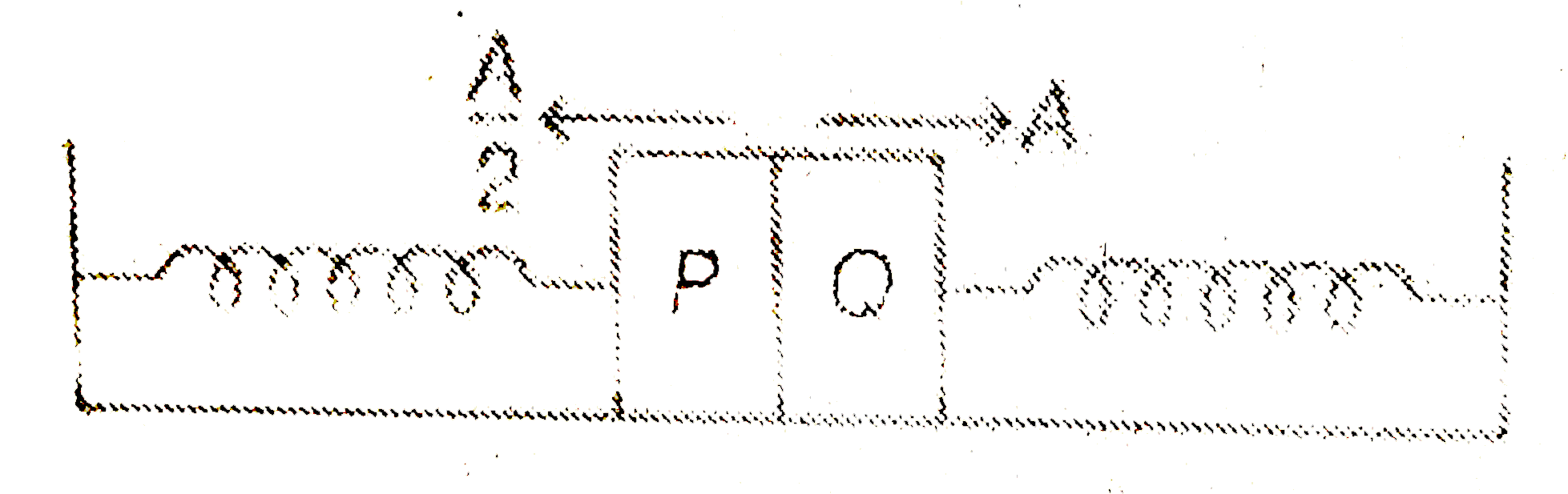
The time period of oscillation of combined mass is
View SolutionPassage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by `A/2` and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
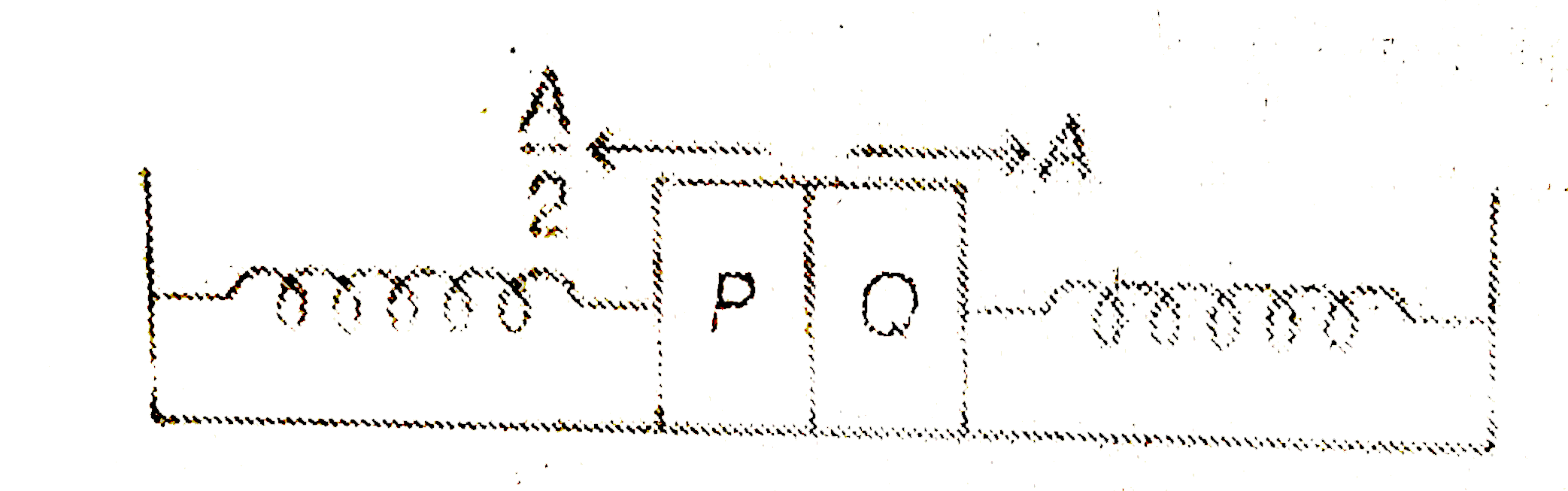
The amplitude of combined mass is
View SolutionPassage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by `A/2` and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
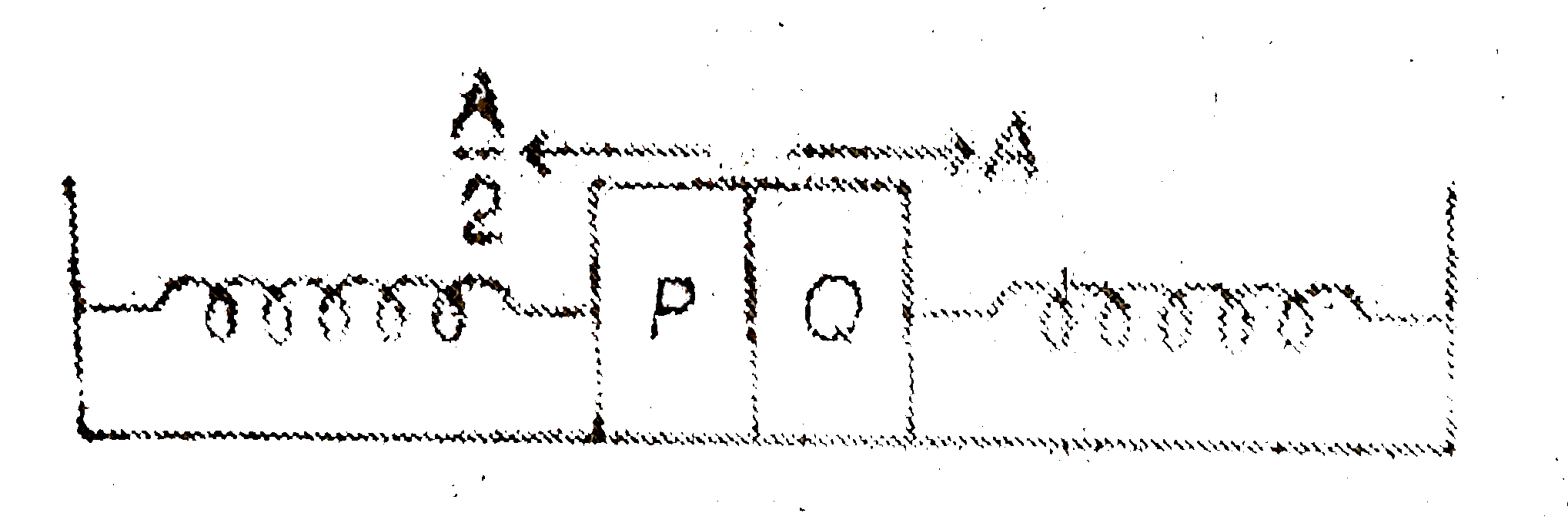
What is energy of osciallation of the combined mass?
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
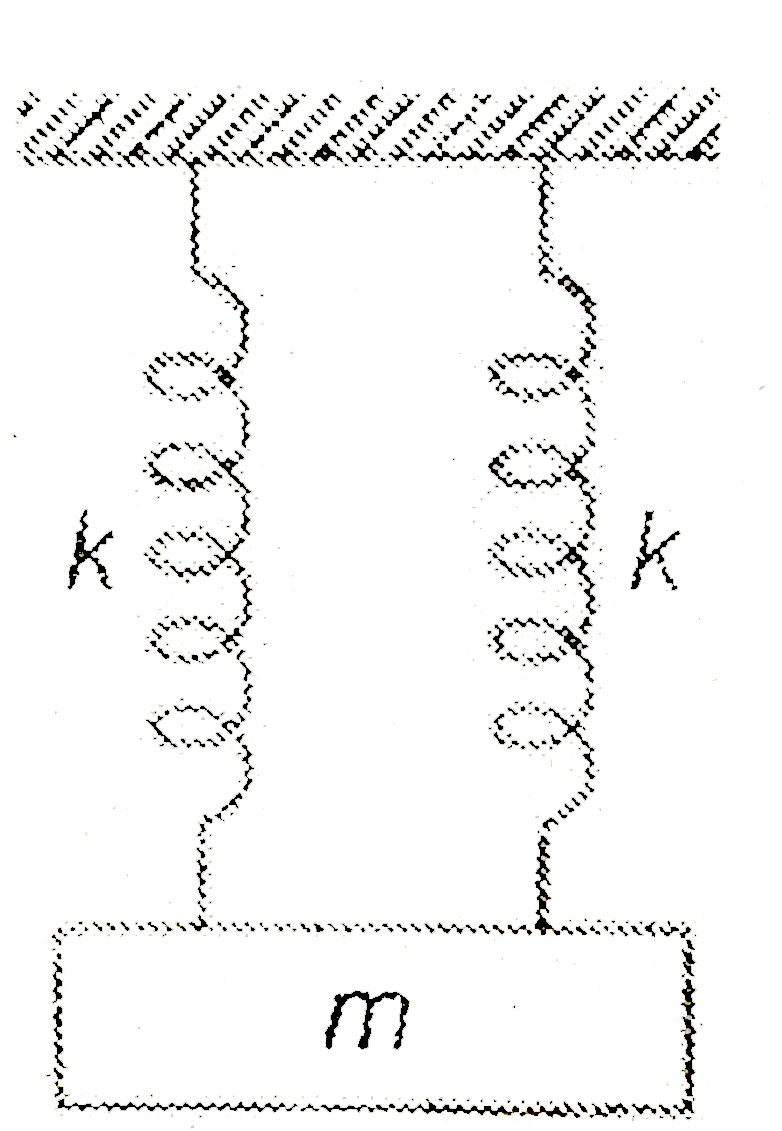
What is the new amplitude of osciallation of the block.
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
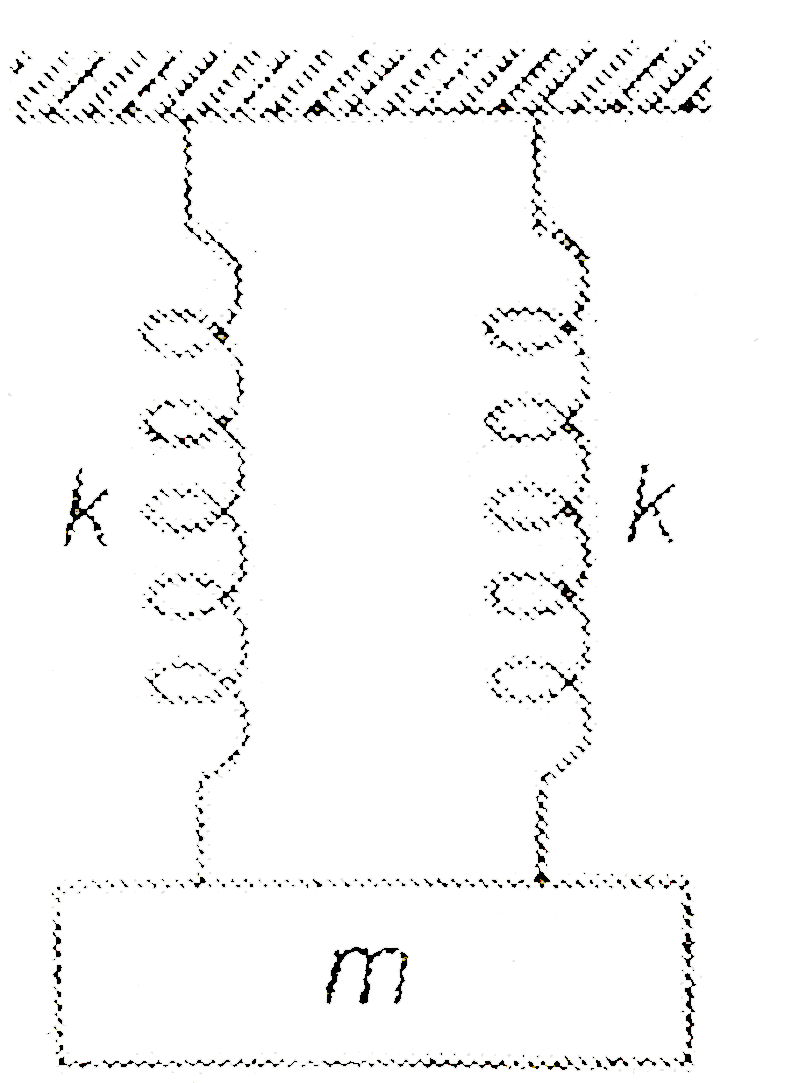
If instead of breaking one spring m/2 mass would have fallen from the block, then what will be the new amplitude?
View SolutionPassage IV) Angular frequency in SHM is given by `omega=sqrt(k/m)`. Maximum acceleration in SHM is `omega^(2)` A and maximum value of friction between two bodies in contact is `muN`, where N is the normal reaction between the bodies.
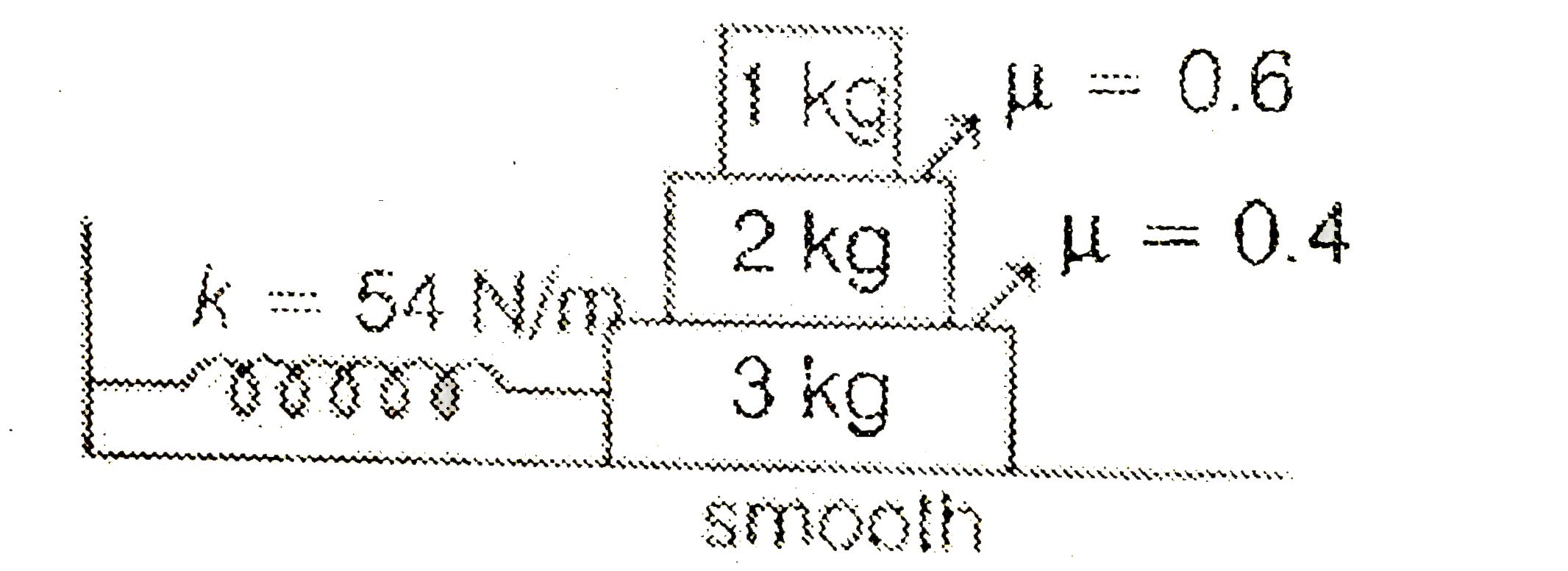
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?
View SolutionAngular frequnecy in SHM is given by `omega = sqrt((k)/(m))`, Maximum acceleration in `SHM` is `omega^(2)A` and maximum value of frication between two bodies in contact is `muN`, where ?N is the normal reaction between the bodies.
Now the value of k, the force constant is increased then the maximum amplitude calculated in above question will :-
View SolutionPassage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency `omega`. Phase difference between any two is `pi/2` except that between displacement and acceleration which is `pi`.
v-t graph of a particle is SHM is as shown in figure Choose the wrong option.

View SolutionPassage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency `omega`. Phase difference between any two is `pi/2` except that between displacement and acceleration which is `pi`.
Displacement -time equation of a particle is given as `x=Asin(omegat+pi/6)-A cos(omegat+pi/6)`, then:
View SolutionPassage VI Two particles collide when they are at same position at same time.
Displacement time equation of two particles moving along x-axis are `x_(1)=(8+3sinomegat)m`
and `x_(2)=(4cosomegat)m`
Here, `omega=pirad/s`
The two particles will collide after time t=...................s.
View SolutionPassage VI Two particles collide when they are at same position at same time.
Displacement time equation of two particles moving along x-axis are `x_(1)=(8+3sinomegat)m`
and `x_(2)=(4cosomegat)m`
Here, `omega=pirad/s`
The two particles will collide after time t=...................s.
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration `a=g/2`
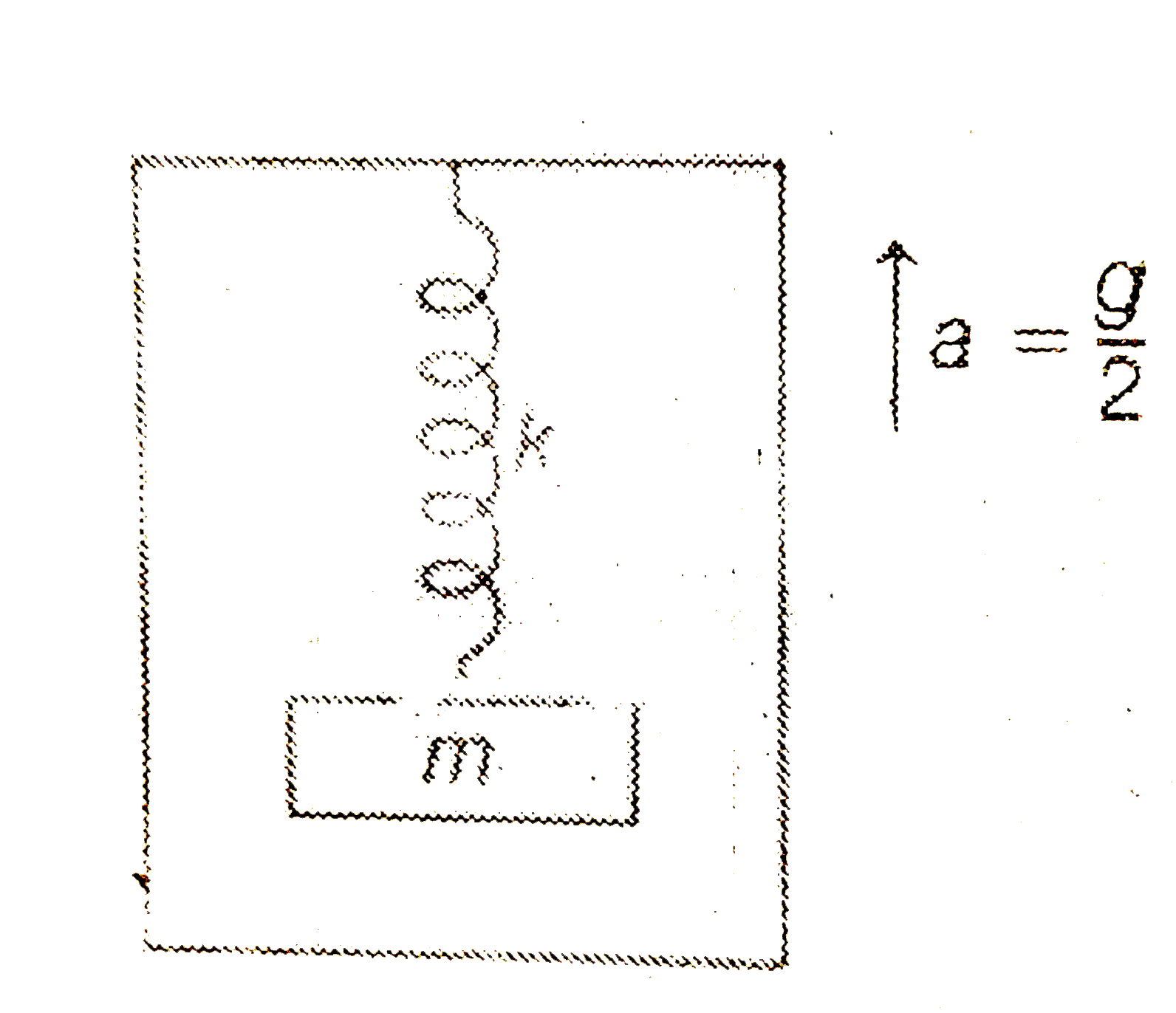
In mean position (of block's oscillations) spring is
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration `a=g/2`

If maximum extension in the spring is `(5mg)/(2k)`, then maximum upward accleration `(a_(1))` and maximum downward acceleration `(a_(2)` of the block are
View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
View SolutionIn the problem if k = 10 N/m, m=2kg, R=1m and A=2m. Find linear speed of the disc at mean position.

View Solution
Comprehension types questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct