Complete Solutions to Level 2 Single Correct of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
A particle of mass `2 kg` moves in simple harmonic motion and its potential energy `U` varies with position `x` as shown. The period of oscillation of the particle is

View SolutionIn the figure shown, a spring mass system is placed on a horizontal smooth surface in between two vertical rigid walls `W_(1)` and `W_(2)`. One end of spring is fixed with wall `W_(1)` and other end is attached with mass `m` which is free to move. Initially, spring is tension free and having natural length `l_(0)`. Mass `m` is compressed through a distance a and released. Taking the collision between wall `W_(2)` and mass `m` as elastic and `K` as spring constant, the average force exerted by mass `m` on wall `W_(2)` in one oscillation of block is

View SolutionTwo simple harmonic motion are represrnted by the following equation `y_(1) = 40 sin omega t` and `y_(2) = 10 (sin omega t + c cos omega t)`. If their displacement amplitudes are equal, then the value of `c` (in appropriate units) is
View SolutionA particle executes simple harmonic motion with frequqncy `2.5Hz` and amplitude `2 m`. The speed of the particle `0.3 s` after crossing, the equilibrium position is
View SolutionA particle oscillates simple harmonic motion with a period of `16 s`. Two second after crossing the equilibrium position its velocity becomes `1 m//s`. The amplitude is
View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of `4 m//s^(2)` . Its period of oscillation is
View SolutionA particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are `a` and `v` respectively, identify the graph which correctly represents the relation between `a` and `v`.
View SolutionIn a vertical `U` - tube a column of mercury oscillates simple harmonically. If the tube contains `1kg` of mercury and `1cm` of mercury column weighs `20 g`, then the period of oscillation is
View SolutionA solid cube of side a and density `rho_(0)` floats on the surface of a liquid of density `rho`. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA uniform stick of length `l` is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance `d` from the centre of mass. The time period of small oscillation has a minimum value when `d//l` is
View SolutionThree arrangements of spring - mass system are shown in figures (A), (B) and ( C). If `T_(1)`, `T_(2)` and `T_(3)` represent the respective periods of oscillation, then correct relation is
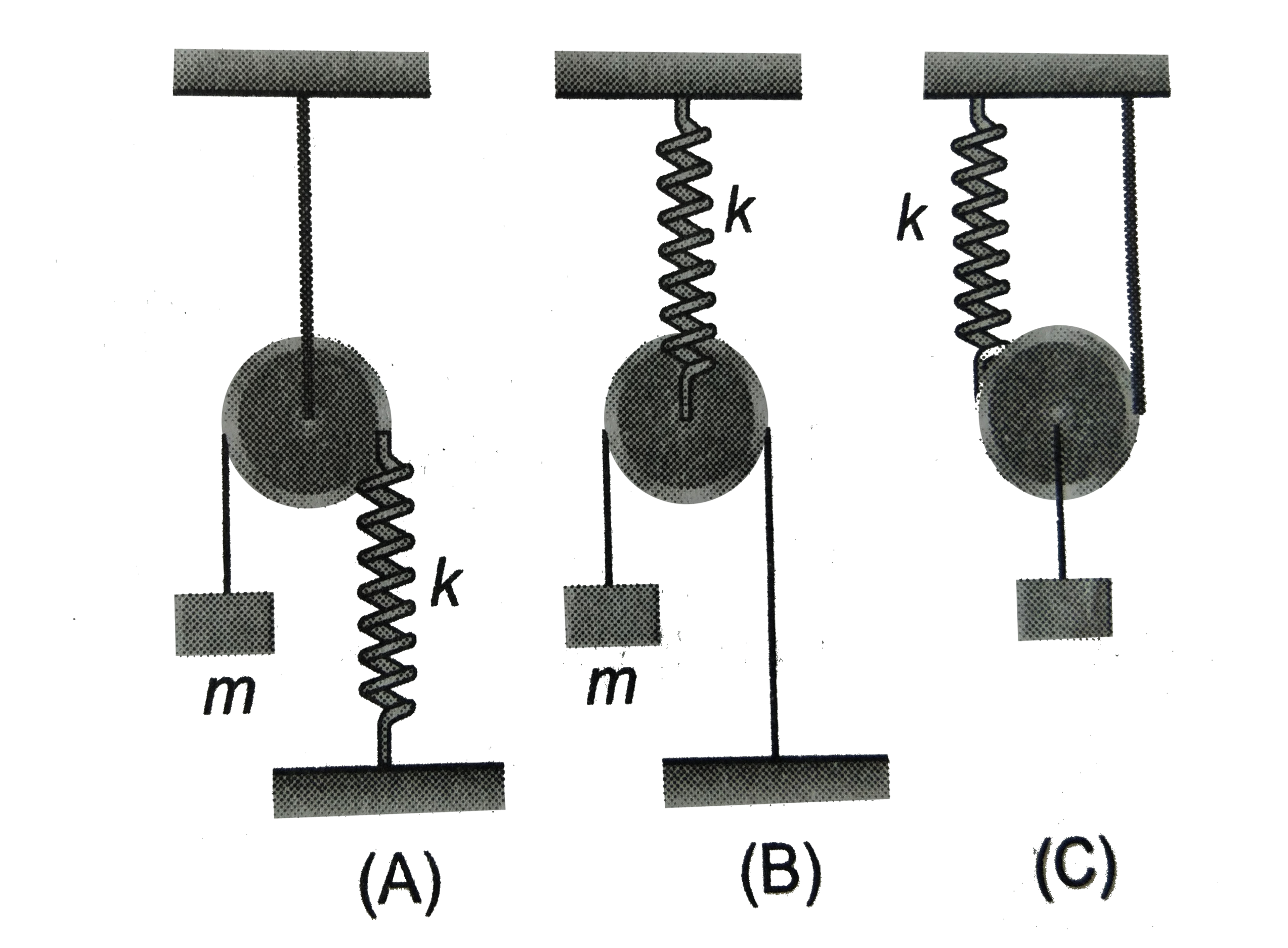
View SolutionThree arrangements are shown in figure.
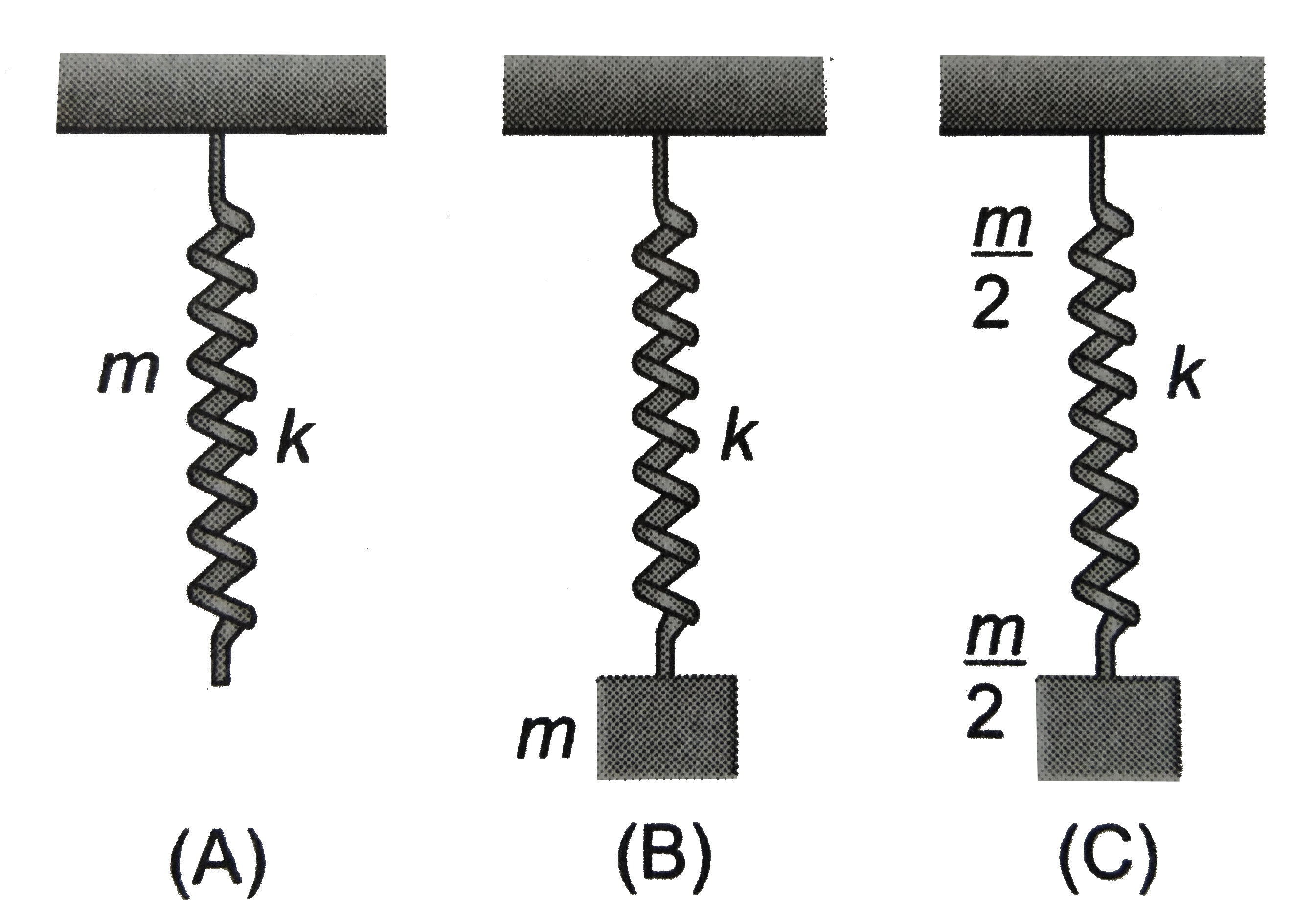
(a) A spring of mass `m` and stiffness `k`
(b) A block of mass `m` attached to massless spring of stiffness `k`
( c) A block of mass `(m)/(2)` attached to a spring of mass `(m)/(2)` and stiffness `k`
If `T_(1)`, `T_(2)` and `T_(3)` represent the period of oscillation in the three cases respectively, then identify the correct relation.
View SolutionA block of mass `M` is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted `(l_(0)//2)` from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

View SolutionA particle moving on x - axis has potential energy `U = 2 - 20x + 5x^(2)` joule along x - axis. The particle is relesed at `x = -3`. The maximum value of `x` will be (`x` is in metre)
View SolutionA block of mass `m`, when attached to a uniform ideal apring with force constant `k` and free length `L` executes SHM. The spring is then cut in two pieces, one with free length n `L` and other with free length `(1 - n)L`. The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency `f_(1)` . The bigger part of the block attached to smaller part of the spring executes SHM with frequency `f_(2)`. The ratio `f_(1)//f_(2)` is
View SolutionA body performs simple harmonic oscillations along the straight line `ABCDE` with `C` as the midpoint of `AE`. Its kinetic energies at `B` and `D` are each one fourth of its maximum value. If `AE = 2R`, the distance between `B` and `D` is

View SolutionIn the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
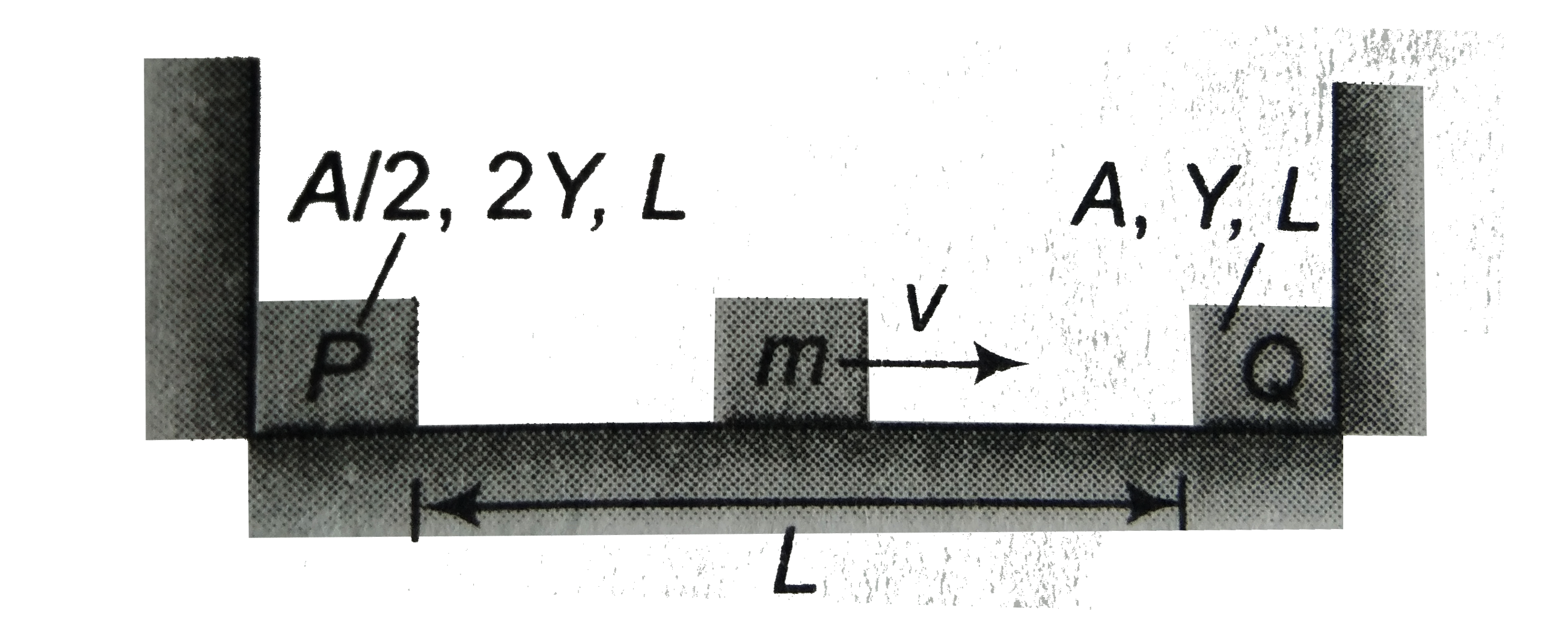
View SolutionA particle executes SHM of period `1.2 s` and amplitude `8cm`. Find the time it takes to travel `3cm` from the positive extremity of its oscillation. `[cos^(-1)(5//8) = 0.9rad]`
View SolutionA wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the `Delta` always remaining vertical. The side of the frame is `1//sqrt(3)m`. The time period in seconds of small oscillations of the frame will be-
View SolutionA particle moves along the x - axis according to `x = A[1 + sin omega t]`. What distance does is travel in time interval from `t = 0` to `t = 2.5pi//omega` ?
View SolutionA small bob attached to a light inextensible thread of length `l` has a periodic time `T` when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end `O` of a vertical rigid rod of length `3l//4`. If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be

View SolutionA stone is swinging in a horizontal circle of diameter `0.8m` at `30 rev//min`. A distant light causes a shadow of the stone on a nearly wall. The amplitude and period of the SHM for the shadow of the stone are
View SolutionPart of SHM is graphed in the figure. Here, `y` is displacement from mean position. The correct equation describing the SHM is
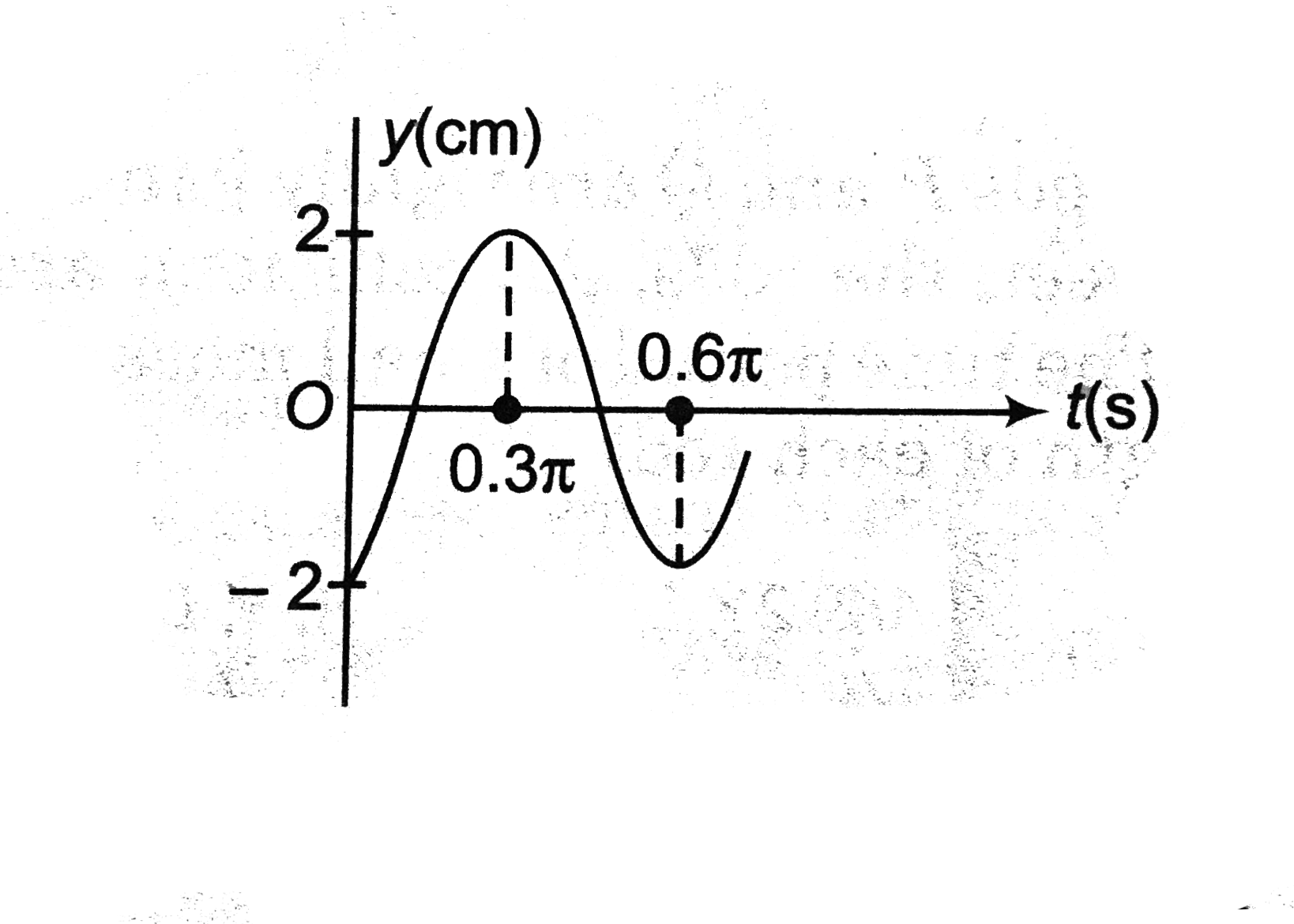
View SolutionA particle performs SHM with a period `T` and amplitude a. The mean velocity of particle over the time interval during which it travels `a//2` from the extreme position is
View SolutionA man of mass `60kg` is standing on a platform executing SHM in the vertical plane. The displacement from the mean position varies as `y = 0.5sin(2pift)`. The value of `f`, for which the man will feel weightlessness at the highest point, is (`y` in metre)
View SolutionA particle performs SHM on a straight line with time period `T` and amplitude`A`. The average speed of the particle between two successive instants, when potential energy and kinetic energy become same is
View SolutionThe time taken by a particle performing SHM to pass from point `A` to `B` where its velocities are same is `2 s`. After another `2 s` it returns to `B`. The ratio of distance `OB` to its a amplitude (where `O` is the mean position) is
View SolutionA particle is executing SHM according to the equation `x = A cos omega t`. Average speed of the particle during the interval `0 le t le (pi)/(6omega)` is
View Solution
Level 2 Single Correct questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct