Complete Solutions to Level 1 Single Correct of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Level 1 Single Correct |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A simple harmonic oscillation has an amplitude `A` and time period `T`. The time required to travel from `x = A` to ` x= (A)/(2)` is
View SolutionThe potential energy of a particle executing SHM varies sinusoidally with frequency `f`. The frequency of oscillation of the particle will be
View SolutionFor a particle undergoing simple harmonic motion, the velocity is plotted against displacement. The curve will be
View SolutionA simple pendulum is made of bob which is a hollow sphere full of sand suspended by means of a wire. If all the sand is drained out, the period of the pendulum will
View SolutionTwo simple harmonic motions are given by `y_(1) = a sin [((pi)/(2))t + phi]` and `y_(2) = b sin [((2pi)/( 3))t + phi]`. The phase difference between these after `1 s` is
View SolutionA particle starts performing simple harmonic motion. Its amplitude is `A`. At one time its speed is half that of the maximum speed. At this moment the displacement is
View SolutionWhich of the following is not simple harmonic function ?
View SolutionThe displacement of a particle varies according to the relation `x=4 (cos pit+ sinpit)`. The amplitude of the particle is.
View SolutionTwo pendulums `X` and `Y` of time periods `4 s` and `4.2s` are made to vibrate simultaneously. They are initially in same phase. After how many vibration of `X`, they will be in the same phase again ?
View SolutionA mass `M` is suspended from a massless spring. An additional mass `m` stretches the spring further by a distance `x`. The combined mass will oscillate with a period
View SolutionTwo bodies `P` and `Q` of equal masses are suspended from two separate massless springs of force constants `k_(1)` and `k_(2)` respectively. If the two bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitude of `P` to that of `Q` is
View SolutionA disc of radius `R` is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
View SolutionIdentify the correct variation of potential energy `U` as a function of displacement `x` from mean position (or `x^(2)`) of a harmonic oscillator (`U` at mean position `= 0`)
View SolutionIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
View SolutionThe displacement - time `(x - t)` graph of a particle executing simple harmonic motion is shown in figure. The correct variation of net force F action on the particle as a function of time is
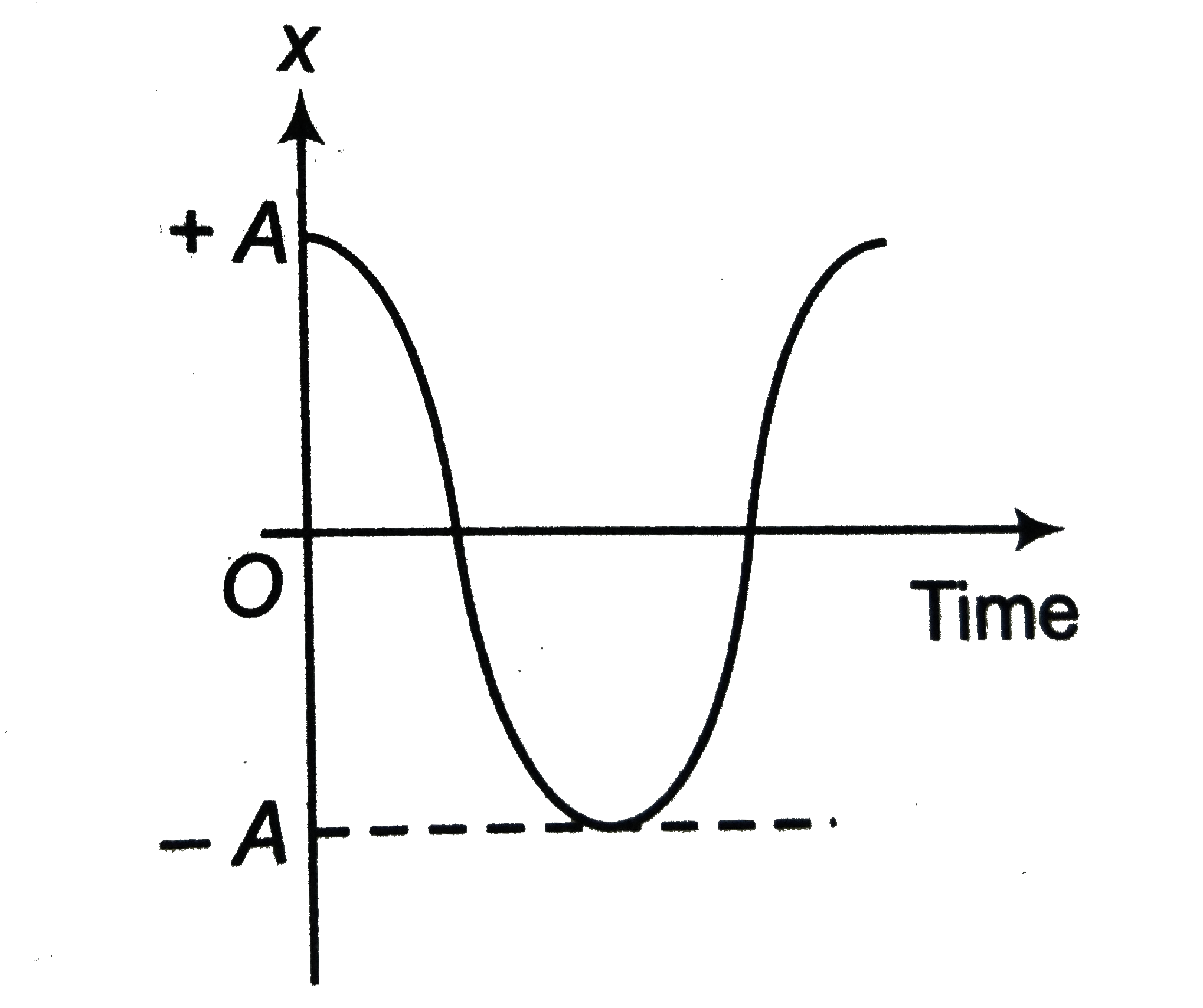
View SolutionIn the figure shown the time period and the amplitude respectively, when `m` is left from rest when spring is relaxed are (the inclined plane is smooth)

View SolutionThe equation of motion of a particle of mass `1g` is `(d^(2)x)/(dt^(2)) + pi^(2)x = 0`, where `x` is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
View SolutionThe spring as shown in figure is kept in a stretched position with extension `x` when the system is relesed. Assuming the horizontal surface to be frictionless, the frequency of oscillation is

View SolutionThe mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this plenet. If is a second's pendulum on earth?
View SolutionThe resultant amplitude due to superposition of three simple harmonic motions `x_(1) = 3sin omega t`,
`x_(2) = 5sin (omega t + 37^(@))` and `x_(3) = - 15cos omega t` is
View SolutionTwo SHMs `s_(1) = a sin omega t` and `s_(2) = b sin omega t` are superimposed on a particle. The `s_(1)` and `s_(2)` are along the direction which makes `37^(@)` to each other
View SolutionThe amplitude of a particle executing SHM about `O` is `10 cm`. Then
View SolutionA particle is attached to a vertical spring and is pulled down a distance `4 cm` below its equilibrium and is released from rest. The initial upward acceleration is `0.5ms^(-2)`. The angular frequency of oscillation is
View SolutionA block of mass `1kg` is kept on smooth floor of a truck. One end of a spring of force constant `100 N//m` is attached to the block and other end is attached to the body of truck as shown in the figure. At `t = 0`, truck begins to move with constant acceleration `2 m//s^(2)`. The amplitude of oscillation of block relative to the floor of truck is
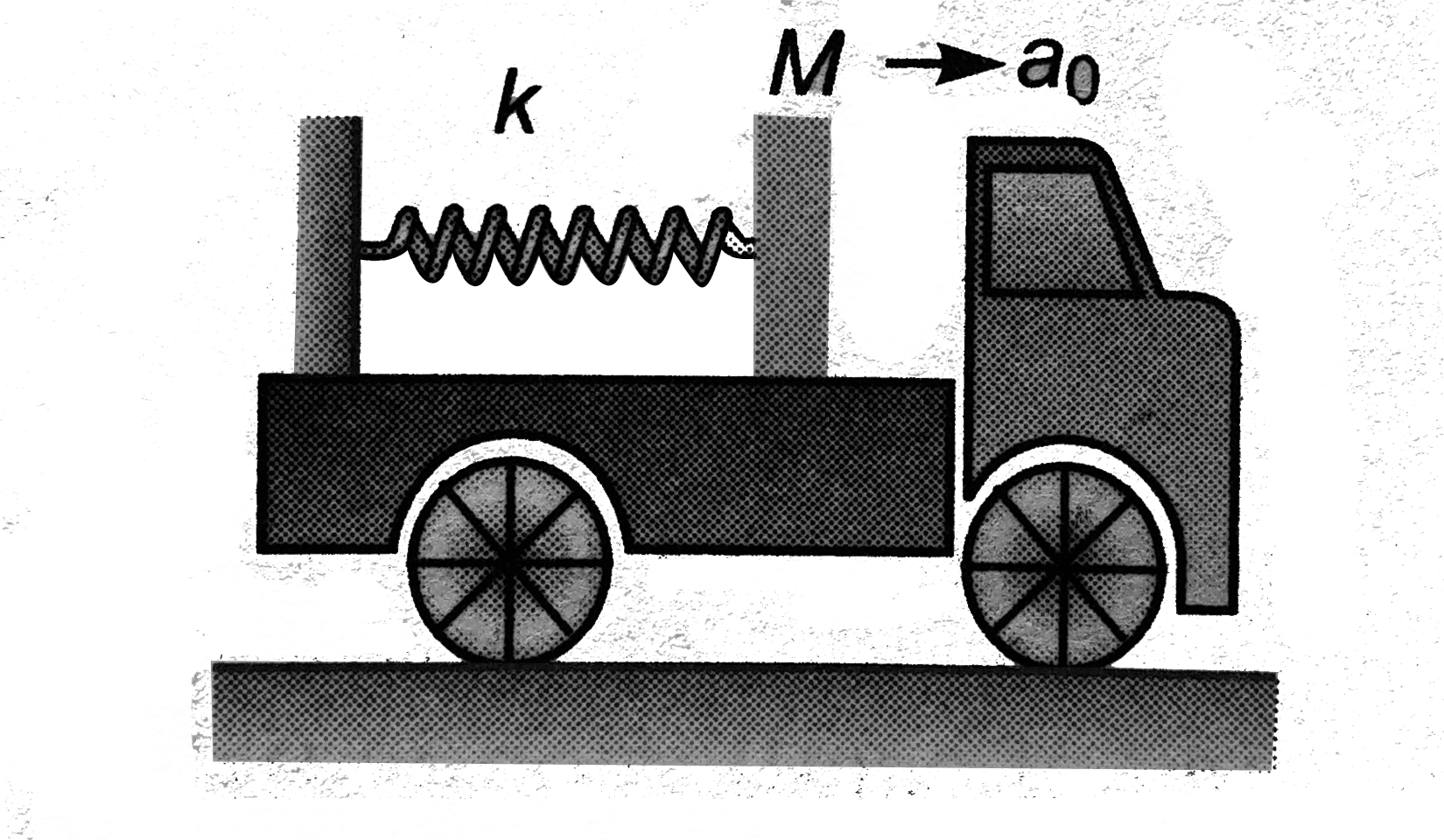
View Solution
Level 1 Single Correct questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct