Complete Solutions to Integer type questions of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | Integer type questions |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Two particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is `sqrt(3)` times their amplitude, the phase difference between them is `(2pi)/n`. Find value of n
View SolutionA particle executes SHM with a frequency of 25 vib/s and has an amplitude of 0.02m. The speed of the particle 0.30 seconds after it is in the equilibrium position is (n`pi`)m/s. Find value of n
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks `mu`=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionForce constant of a weightless spring is 16 N/m. A body of mass 1.0 kg suspended from it is pulled down through 5 cm from its mean position and the released. The maximum kinetic energy of the system (spring+body) will be (0.0x) J. Find value of x.
View SolutionA solid cube floats in water half immersed and has small vertical oscillations of time period `(pi)/(5)` s . Its mass (in kg) is (take , `g=10 ms^(-2)`)
View SolutionA particle under the action of one SHM has a period of 3 s and under the effect of another it has a period 4s. Its time period under the combined action of both the SHM's in the same direction is (0.4x)second. Find value of x?
View SolutionA cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take `pi^(2)`=10 and g=10m/`s^(2)`)
View SolutionA spring has a natural length of 50 cm and a force constant of `2.0 xx 10^(3)` N`m^(-1)`. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/`s^(2)`)
View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction. The amplitude of oscillation is `4 xx 10^(-3)`m. The least period of these oscillations, so that the object is not detached from the platform is `pi/(5x)` second. Find value of x. Take g=10m/`s^(2)`
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is `(npi)/5` second. Find value of n.
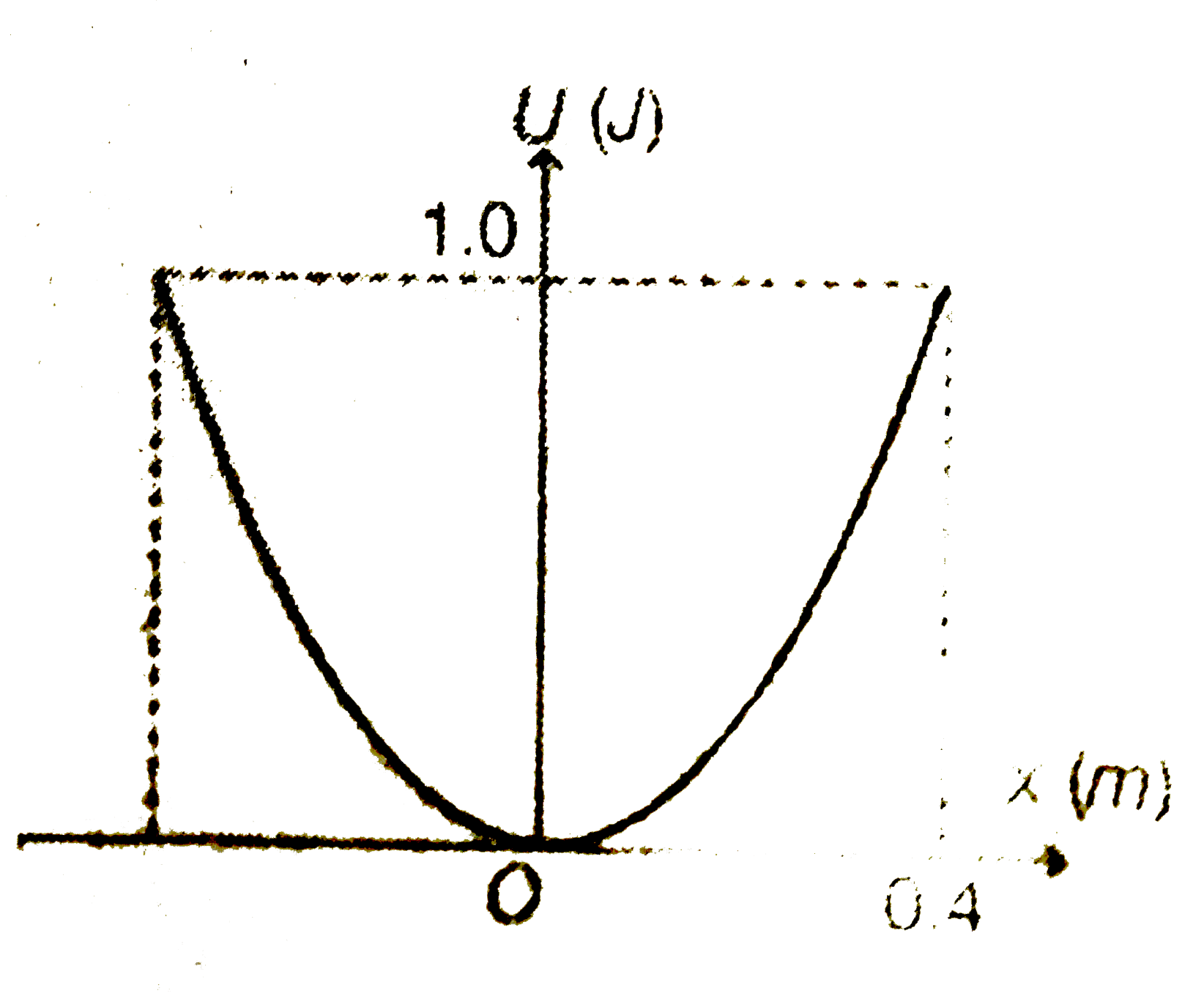
View SolutionA particle performs SHM with a period T and amplitude a. The mean velocity of the particle over the time interval during which it travels a distance `a/2` from the extreme position is `(xa)/(2T)`. Find the value of x.
View SolutionTwo springs of spring constant `(mg)/l` each are attached to the end of a uniform rod of mass m and length `l=5/3`m which is hinged in vertical plane as shown in figure. As the rod is rotated slightly about the hinge, it undergoes SHM with angular frequency `omega`. Find `omega` in rad/s.) Take g`=10m/s^(2)`.
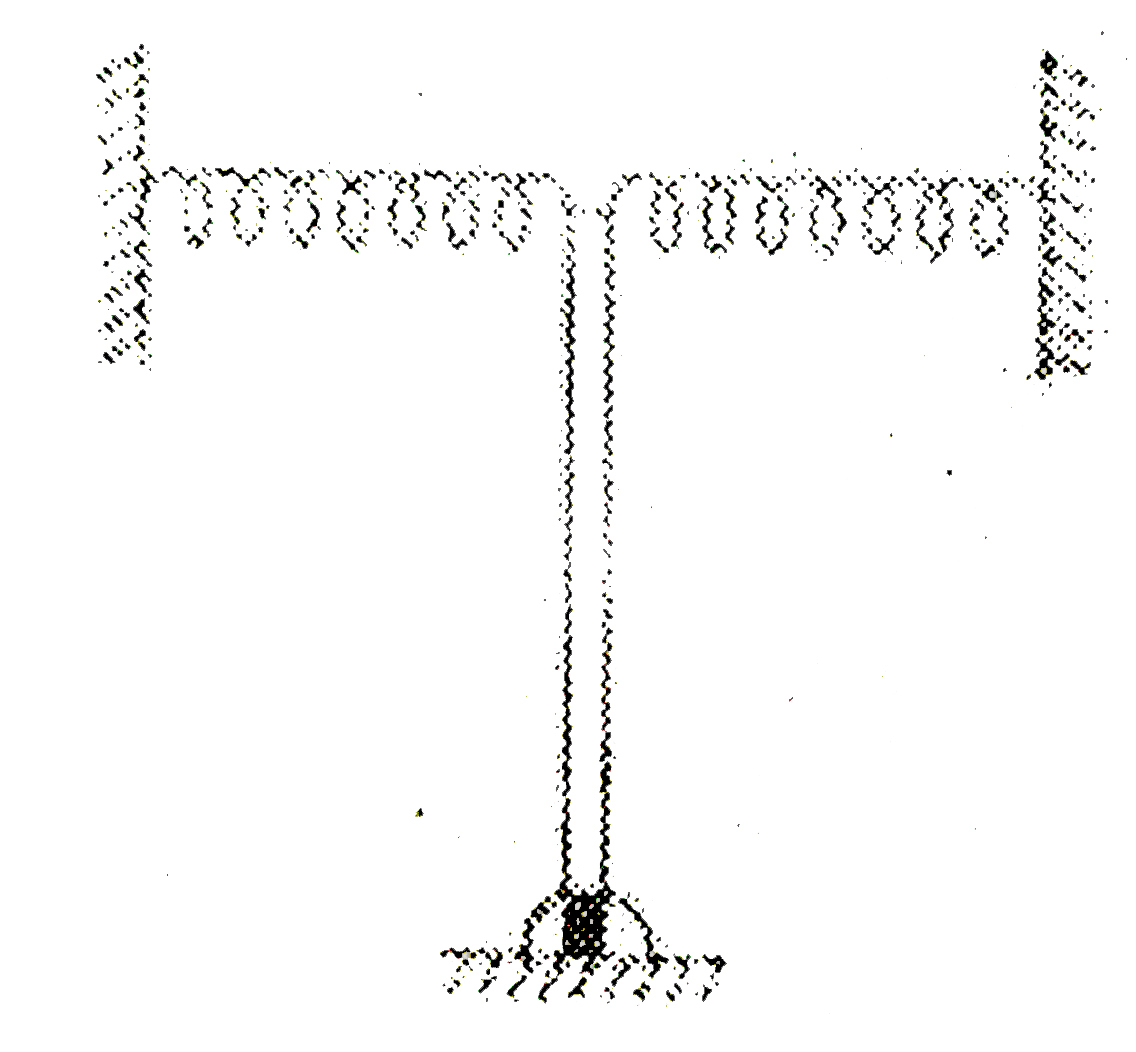
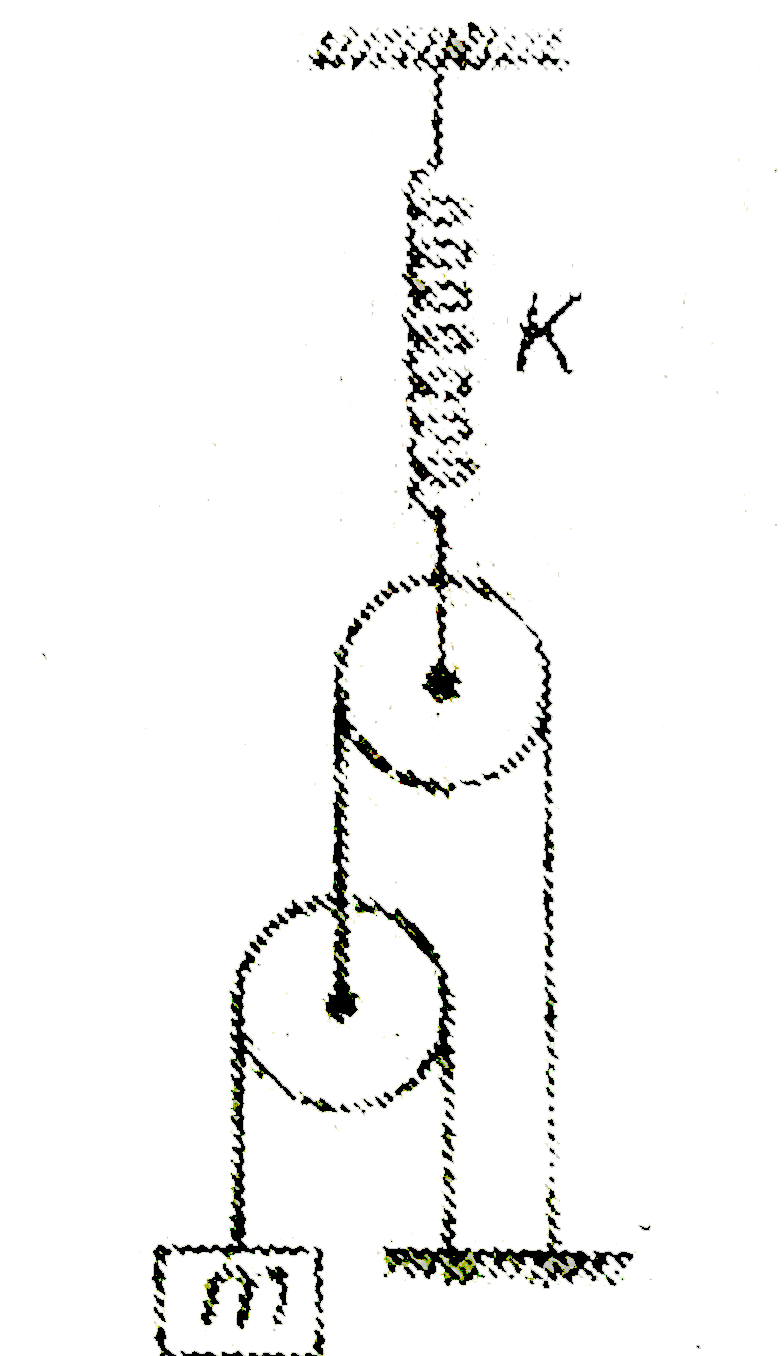
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is `mupisqrt(m/K)`. Then find the value of `mu`.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is `2pisqrt((n(R-r))/(3g))` then find the value of n.

View Solution
Integer type questions questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct