Complete Solutions to Example Type 5 of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Example Type 5 |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
A mass is suspended separately by two springs and the time periods in the two cases are `T_(1)` and `T_(2)`. Now the same mass is connected in parallel `(K = K_(1) + K_(2))` with the springs and the time is suppose `T_(P)`. Similarly time period in series is `T_(S)`, then find the relation between `T_(1),T_(2)` and `T_(P)` in the first case and `T_(1),T_(2)` and `T_(S)` in the second case.
View SolutionTime period of a block with a spring is `T_(0)`. Now ,the spring is cut in two parts in the ratio `2 : 3`. Now find the time period of same block with the smaller part of the spring.
View SolutionWith the assumption of no slipping, determine the mass m of the block which must be placed on the top of a `6 kg` cart in order that the system period is `0.75s`. What is the minimum coefficient of static friction `mu_(s)` for which the block will not slip relative to the cart is displaced `50 mm` from the equilibrium position and released? Take `(g = 9.8 m//s^(2))`.

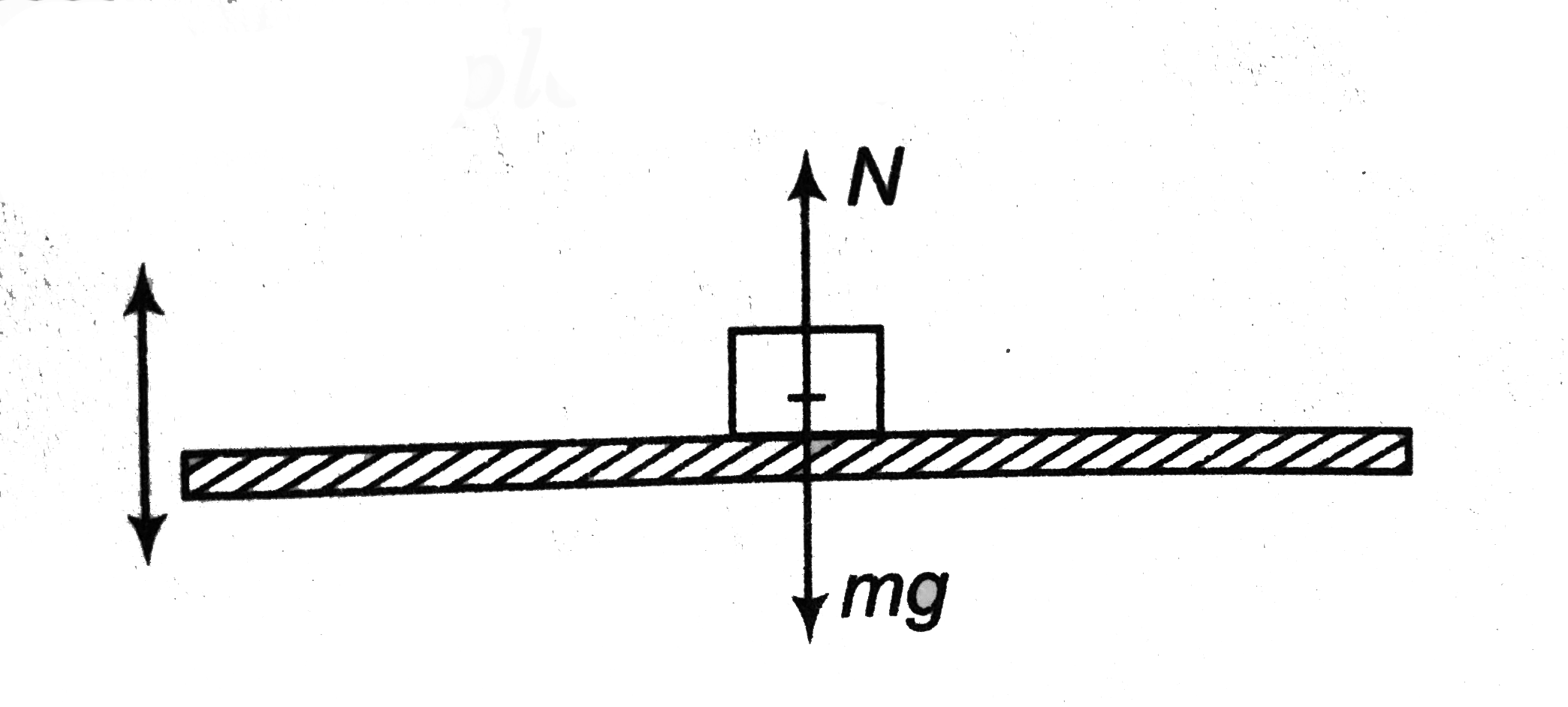
View SolutionA block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency `omega`. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
View SolutionA particle of mass `m` is attached with three springs `A,B` and `C` of equal force constancts `k` as shown in figure. The particle is pushed slightly against the spring `C` and released. Find the time period of oscillation.
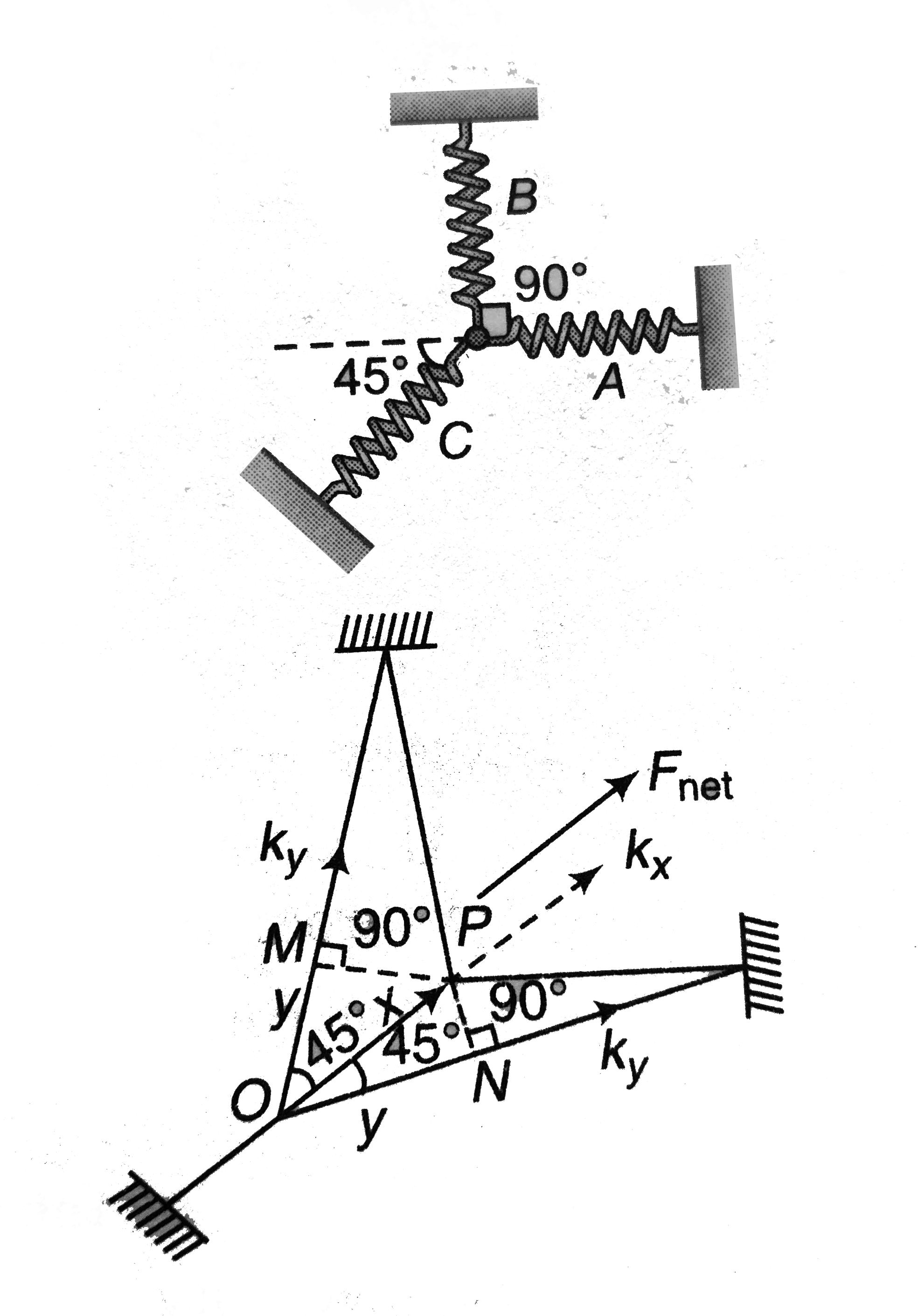 .
.
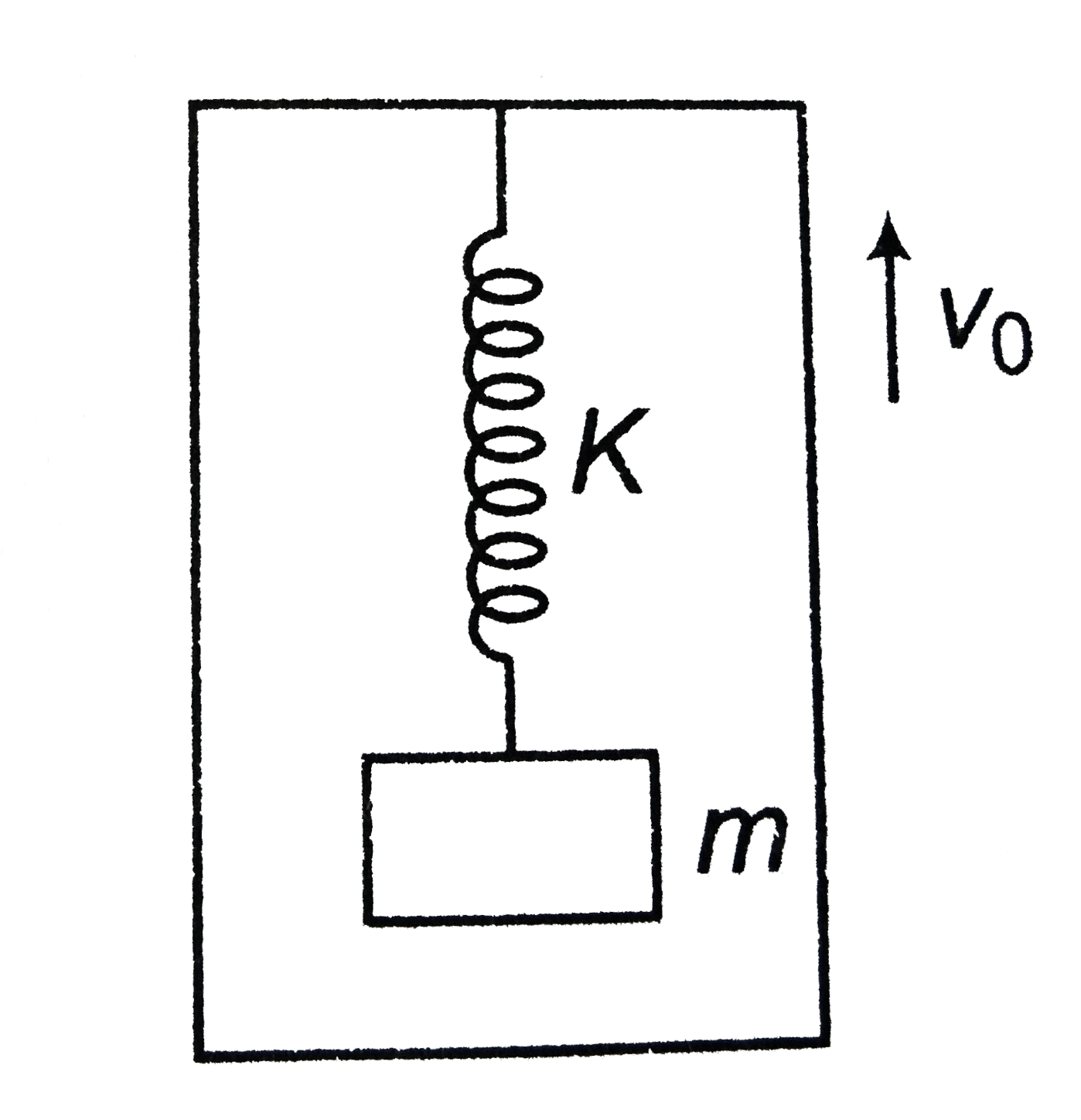
View SolutionA spring block system is kept inside a lift moving with a constant velocity `v_(0)` as shown in figure. Block is in equilibrium and at rest with respect to lift. The lift is suddenly stopped at time `t = 0`. Taking upward direction as the positive direction, write `x - t` equation of the block.
View SolutionOne end of an ideal spring is fixed to a wall at origin `O` and axis of spring is parallel to x-axis. A block of mass `m = 1kg` is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is `x = 10 + 3 sin (10t)`. Here, t is in second and `x` in `cm`. Another block of mass `M = 3kg`, moving towards the origin with velocity `30 cm//s` collides with the block performing SHM at `t = 0` and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View Solution
Example Type 5 questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct