Complete Solutions to More than one option is correct of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | More than one option is correct |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
A particle is executing SHM with amplitude A. At displacement `x=(-A/4)`, force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude `30^(@)`. Then (g=`9.8m//s^(2)`
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionVelocity-time graph of a particle executing SHM is shown in figure. Select the correct alternative(s).

View SolutionAccleration-time graph of a particle executing SHM is as shown in figure. Select the correct alternatives(s).
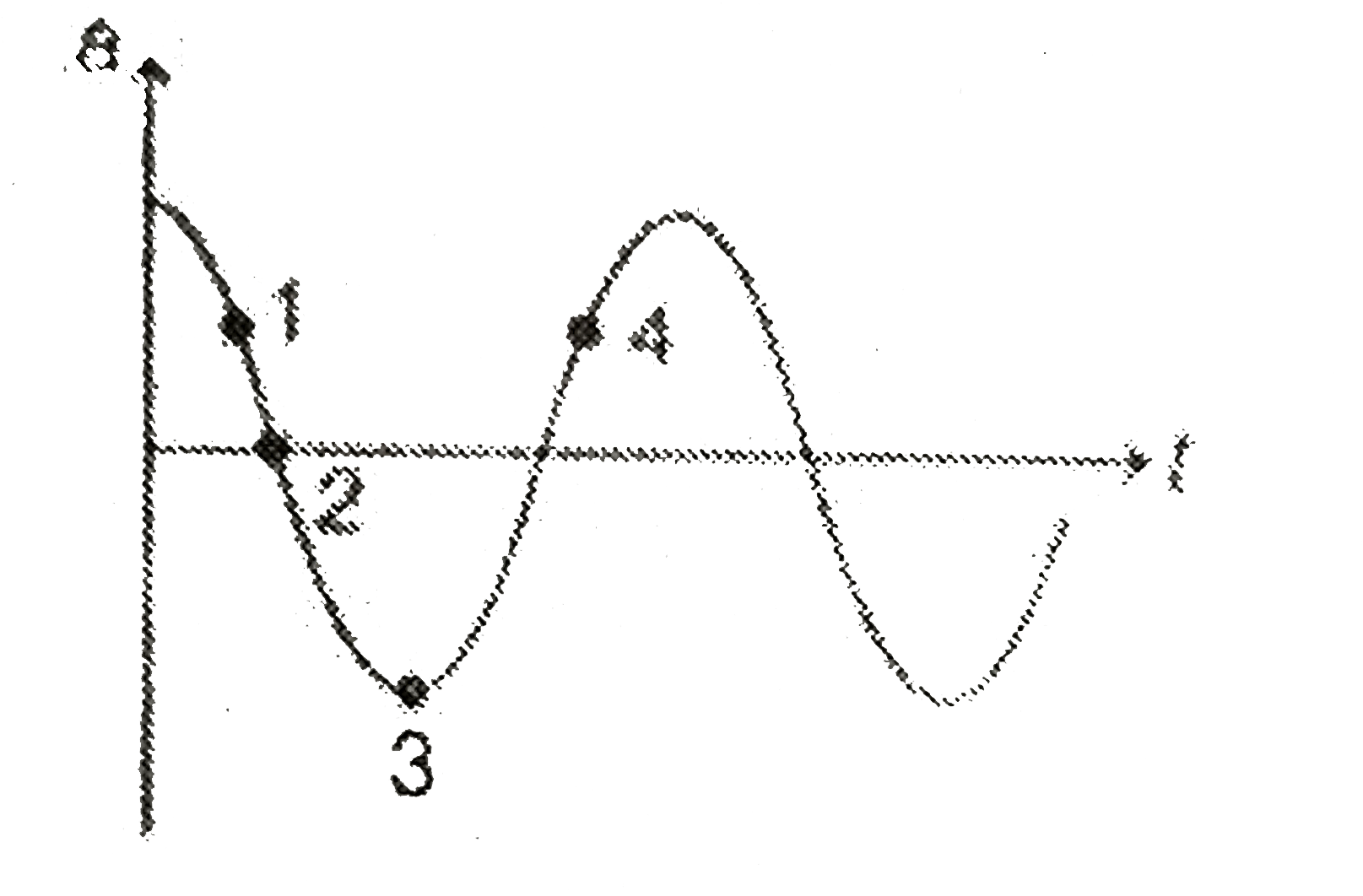
View SolutionDensity of a liquid varies with depth as `rho=alpha`h. A small ball of density `rho_(0)` is released from the free surface of the liquid. Then
View SolutionA particle stars SHM at time t=0. Its amplitude is A and angular frequency is `omega.` At time t=0 its kinetic energy is `E/4`. Assuming potential energy to be zero and the particle can be written as (E=total mechanical energy of oscillation).
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is `v^(2)=144-9x^(2)`. Select the correct alternatives
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=`x_(0) + a sinomegat`. An identical block B moving towards negative x -axis with velocity `v_(0)` collides elastically with block A at time t=0. Then
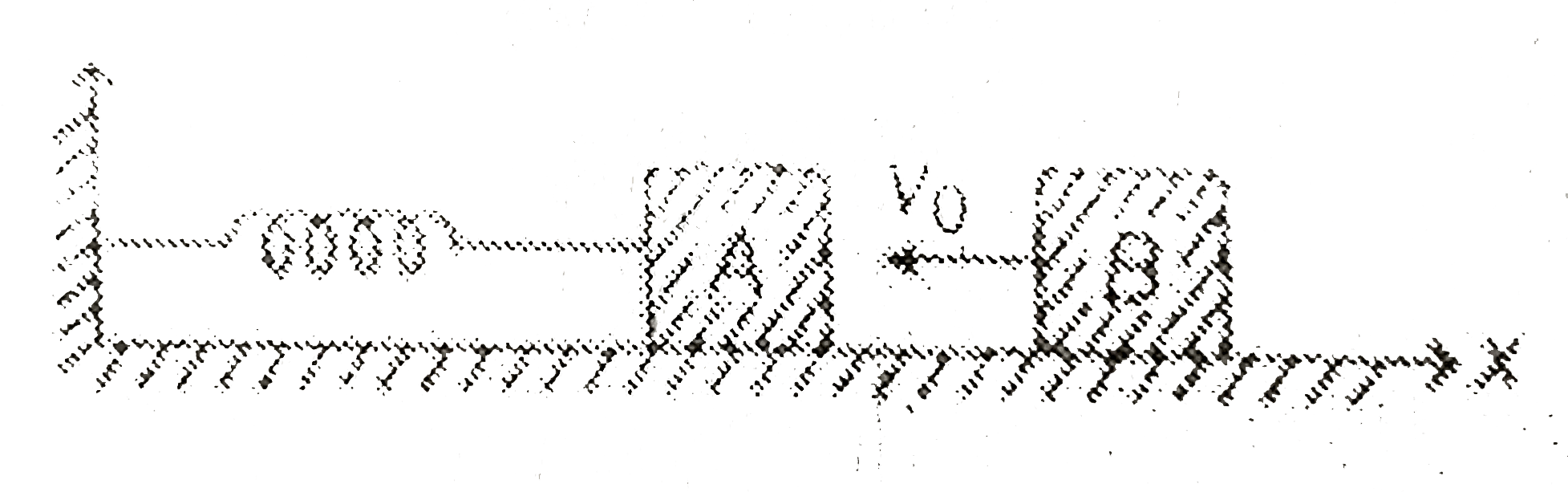
View SolutionA particle moves along the x-axis according to the equation `x=4+3sin(2pit)`
Hence, x in cm and t in seconds. Select the correct alternatives
View SolutionIn simple harmonic motion
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration `a_(0).` As seen from the truck

View SolutionA particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point P(APltBP) at successive intervals of 0.5s and 1.5 s with a speed of 3m/s.
View SolutionTwo particles undergo `SHM` along the same line with the same time period `(T)` and equal amplitude `(A)`. At a particular instant one is at `x =- A` and the other is at `x =0`. If they start moving in the same direction then they will cross each other at

(i) `t = (4T)/(3)` (ii) `t = (3T)/(8)` (iii) `x = (A)/(2)` (iv) `x = (A)/(sqrt(2))`
View SolutionA particle of mass m is moving in a potential well, for which the potential energy is given by `U(x) = U_(0)(1-cosax)` where `U_(0)` and a are positive constants. Then (for the small value of x)
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View Solutionx-t equation of a particle moving along x-axis is given as
`x=A+A(1-cosomegat)`
View SolutionIn simple harmonic motion of a particle, maximum kinetic energy is 40 J and maximum potential energy is 60 J. then
View SolutionTwo particles are in SHM with same amplitude A and same regualr frequency `omega`. At time t=0, one is at x =`+A/2` and the other is at `x=-A/2`. Both are moving in the same direction.
View SolutionTime period of spring-block system on surface of earth is `T_(1)` and that of a simple pendulum is `T_(2)`. At height h = R (the radius of earth) the corresponding values are `T'_(1)` and `T'_(2)` then
View SolutionA linear harmonic oscillator of force constant `2 xx 10^6 N//m` and amplitude (0.01 m) has a total mechanical energy of (160 J). Its.
View SolutionThree simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by `45^(@)`, then
View SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionThe time period of a particle in simple harmonic motion is T. Assume potential energy at mean position to be zero. After a time of `(T)/(6)` it passes its mean position ,then at t=0 its,
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing `SHM`:
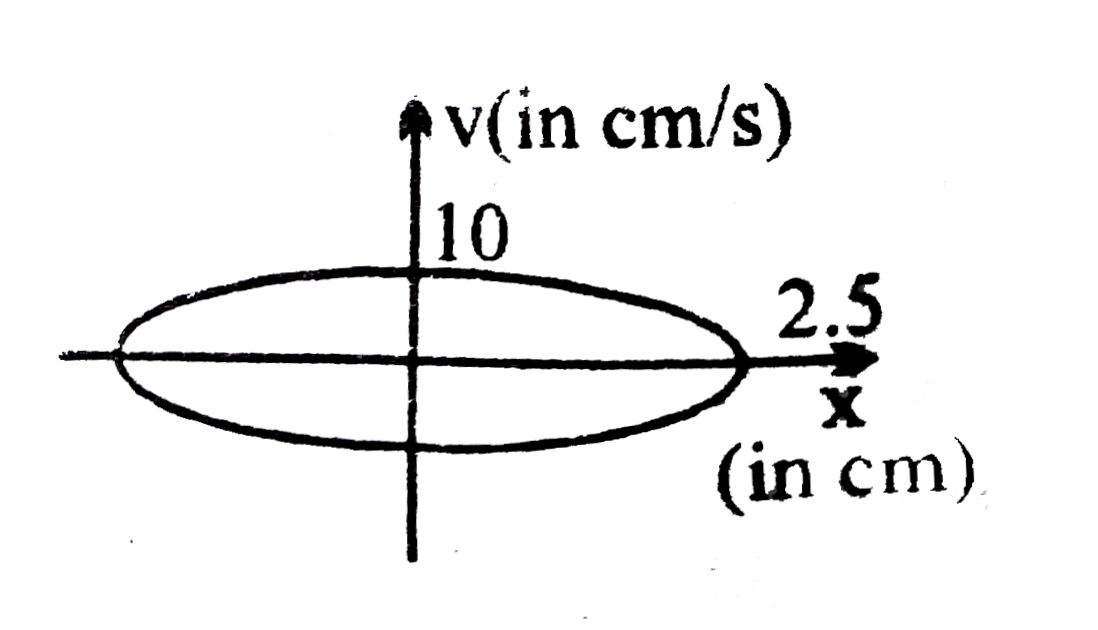
View SolutionTwo blocks of masses 3 kg and 6kg rest on horizontal smooth surface. The 3 kg block is attached to a spring with a force constant `k=900Nm^(-1)` which is compressed 2m from beyond the equilibrium position. The 6 kg mass is at rest at 1m from mean position. 3kg mass strikes the 6 kg mass and the two stick together.

View SolutionTwo springs with negligible massess and force constant of `k_(1)= 200 Nm^(-1)` and `k_(2)=160Nm^(-1)` are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position nor compressed. At time t=0, sharp impulse of 50 N-s is given to the block.
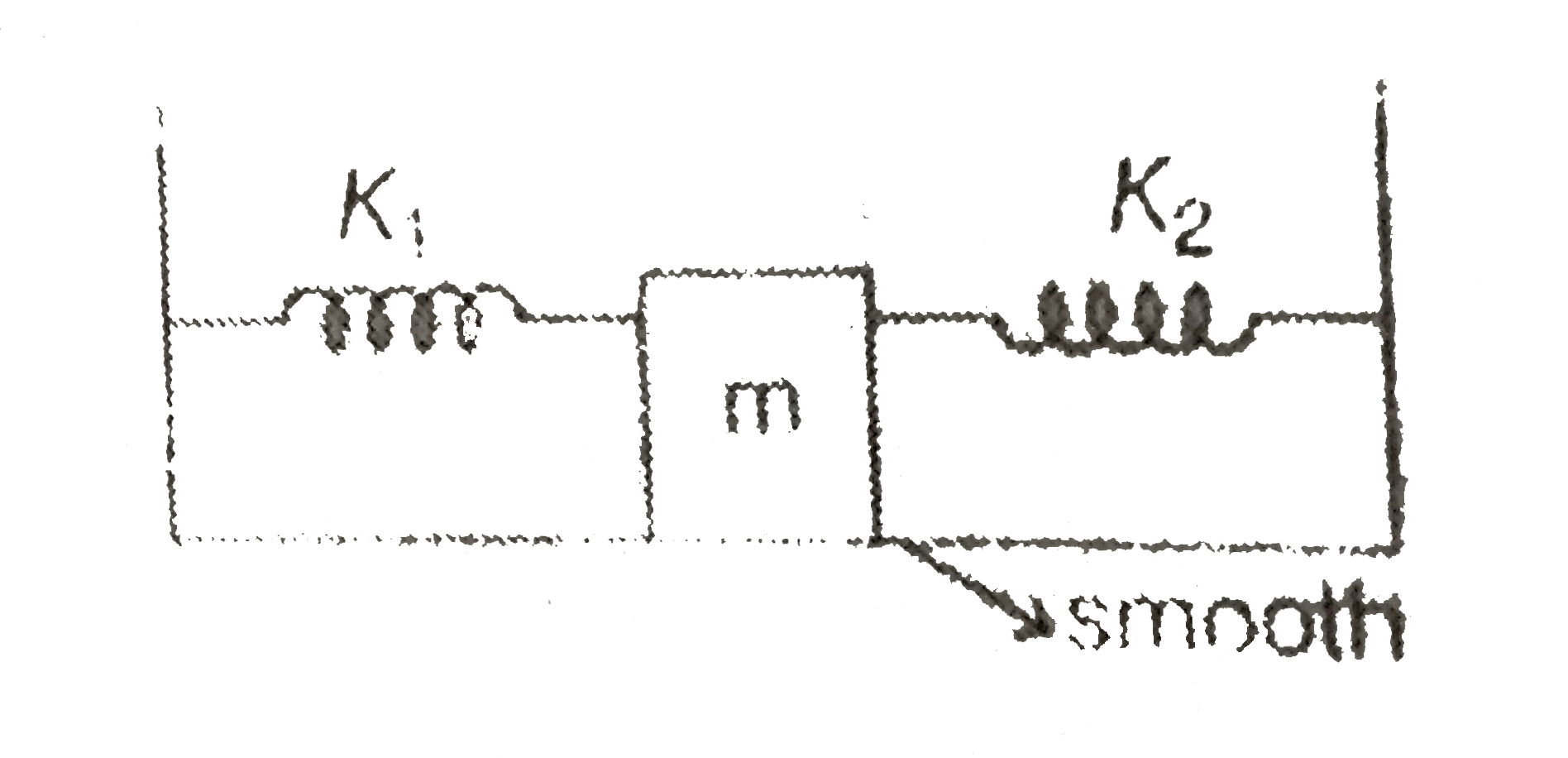
View SolutionInitially spring is compressed by `x_(0)` and blocks are in contact when system is released, then block starts moving and after some time contact between blocks, then
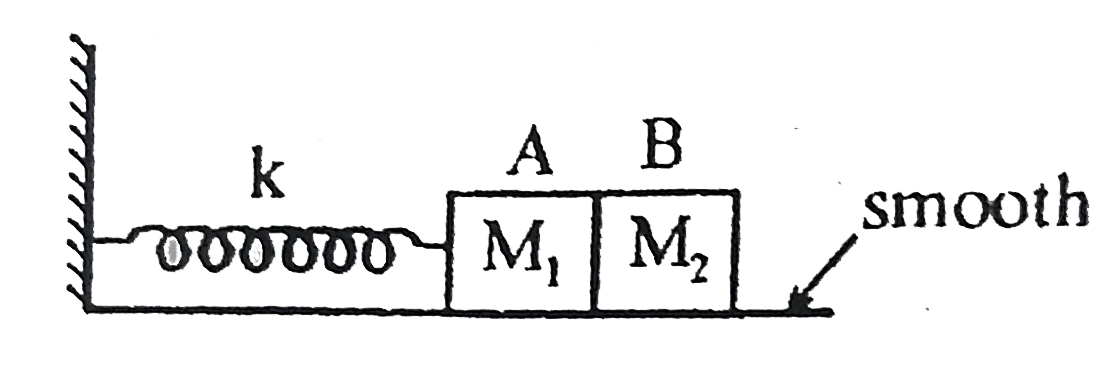
View SolutionA block suspended from a spring is released when the spring is unstretched. Then choose the correct options.

View SolutionTwo smooth tunnels are dug from one side of earth's surface to the other side, one along a diameter are dropped from one end of each of the tunnels. Both particles oscillate simple harmonically along the tunnels. Let `T_(1)` and `T_(2)` be the time period of particles along the diameter and along the chord respectively. Then:
View SolutionTotal energy of a particle executing oscillating motionis 3 joule and given by
`E=x^(2)+2x +v^(2)-2v`
Where x is the displacement from origin at x=0 and v is velocity of particle at x. Then choose the correct statements)
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionIn the figure shown, a block A of mass m is rigidy attached to a light spring of stiffness k and suspended from a fixed support. Another block B of same mass is just placed on it and blocks are in equilibrium. Suddenly the block B is removed. Choose the correct options (s) afterward.
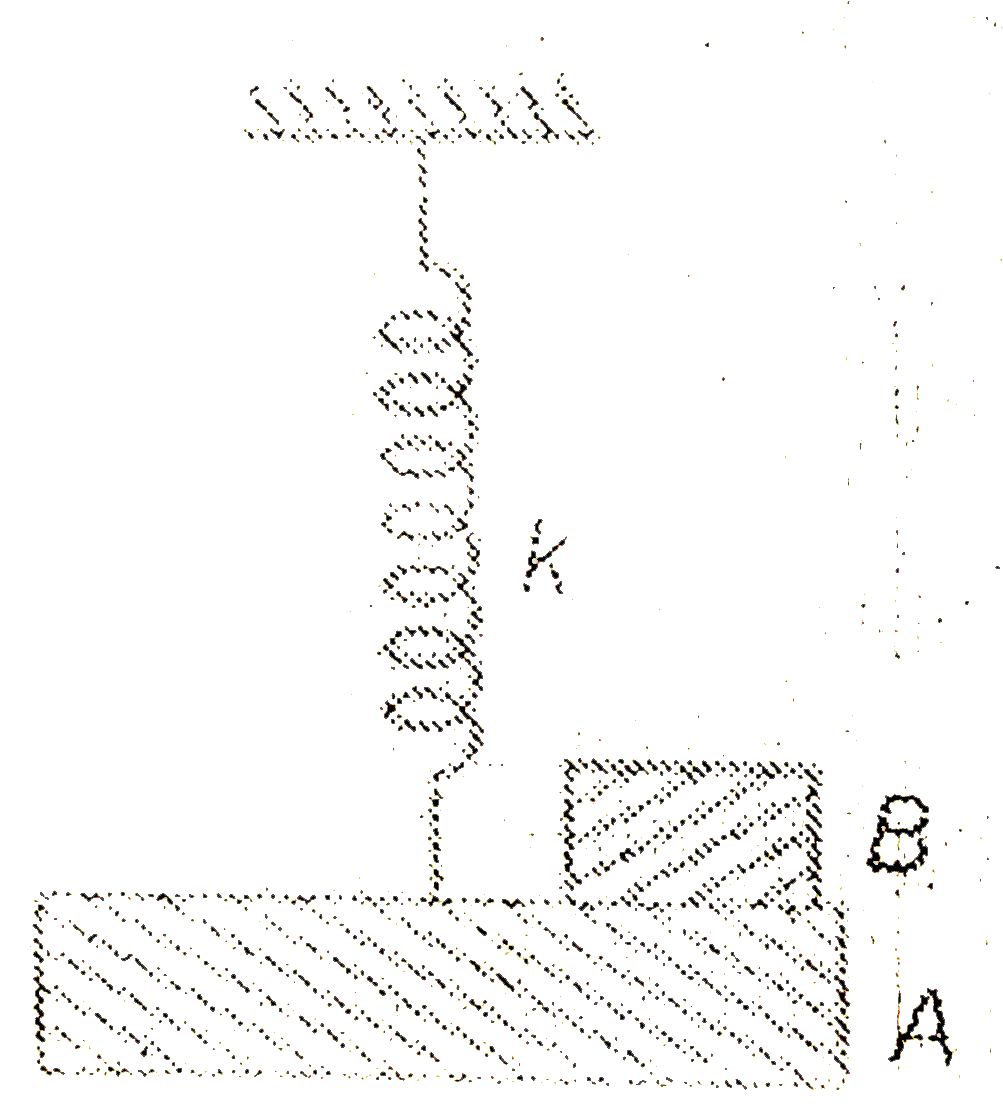
View SolutionPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is `1/2`k`A^(2)`
Force acting on a block is `F=(-4x +8)`. Here F is in Newton and x the position of block on x-axis in meter
View SolutionPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is `1/2`k`A^(2)`
Force acting on a block is F = ( − 4 x + 8 ) .
Here F is in Newton and x the position of block on x-axis in meter If energy of osciallation is 18 J, between what points the block will oscillate?
View SolutionPassage X) A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400 N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of `5m/s^(2)` when the acceleration suddenly ceases at t=0 and the car moves upward with constant speed. (g=10m/`s^(2)`)
What is the angular frequency of oscillation of the block after the acceleration ceases?
View SolutionPassage X) A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400 N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of `5m/s^(2)` when the acceleration suddenly ceases at t=0 and the car moves upward with constant speed. (g=10m/`s^(2)`)
The amplitude of the oscillations is
View SolutionA 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5m/s2 when the acceleration suddenly ceases at time t=0 and the car moves upward with constant speed (g=10m/s2 The amplitude of the oscillation is
View SolutionPassage XI) The differential equation of a particle undergoing SHM is given by `a(d^(2)x)/(dt^(2))`+bx = 0. The particle starts from the extreme position.
The time period of osciallation is given by
View SolutionPassage XI) The differential equation of a particle undergoing SHM is given by `a(d^(2)x)/(dt^(2))`+bx = 0. The particle starts from the extreme position.
The ratio of the maximum acceleration to the maximum velocity of the particle is
View SolutionThe equation of motion may be given by
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
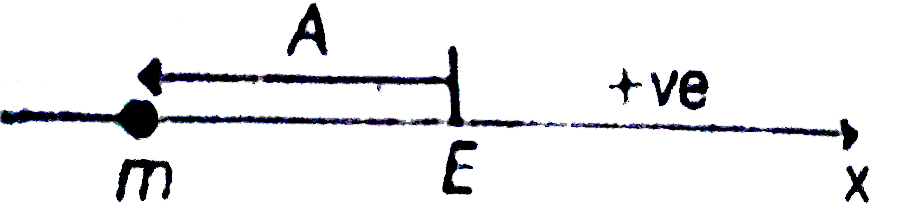
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
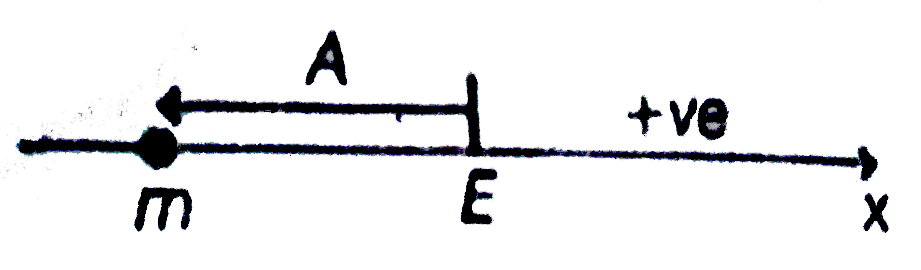
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Find minimum time it will take to reach from x`=-A/2` to 0

View SolutionPassage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 `sec^(-1)` and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take `(pi^(2))` = 10 and g = 10 `m//s^(2)`. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
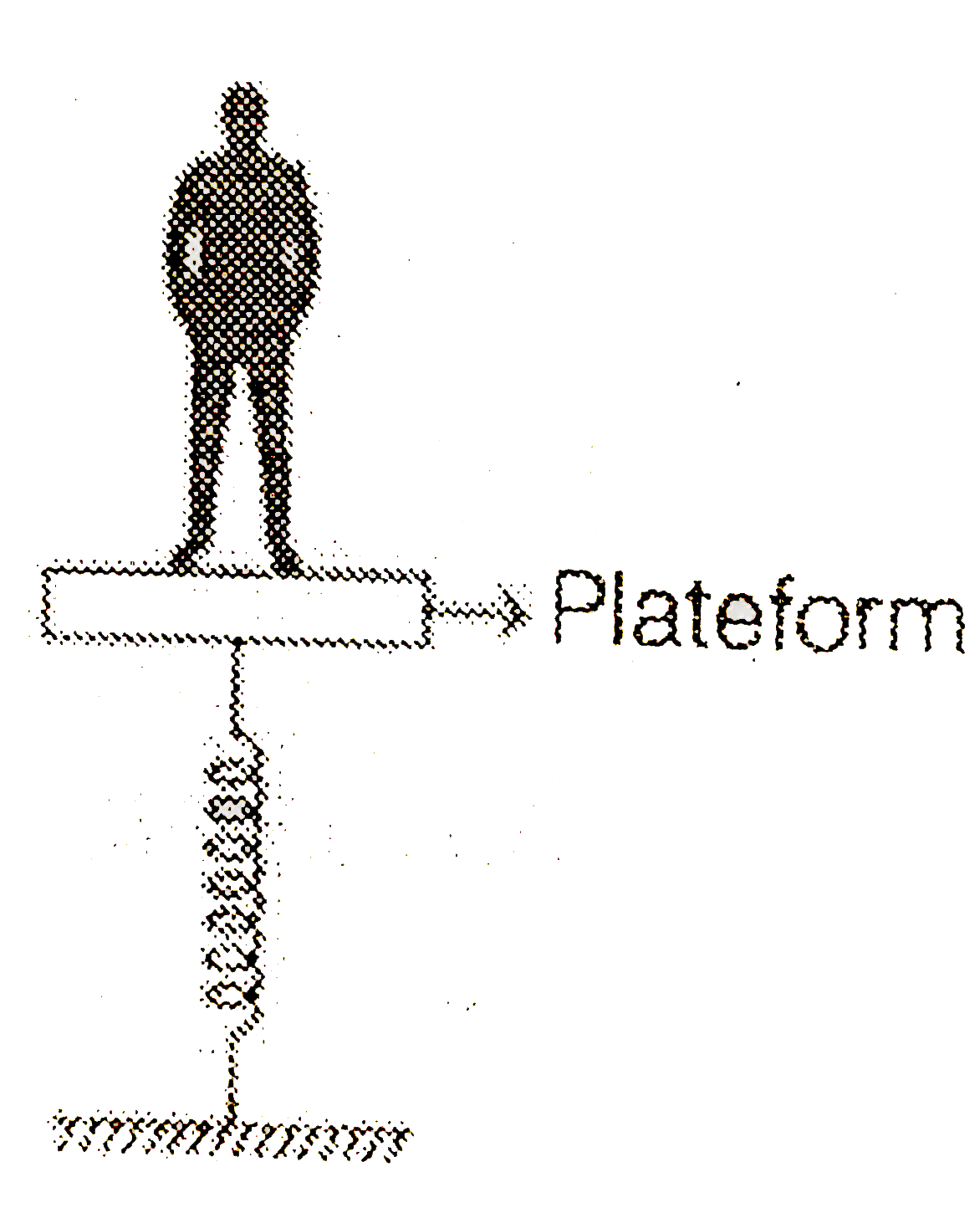
Which of the following will be correct for reading of weighting machine
View SolutionPassage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 `sec^(-1)` and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take `(pi^(2))` = 10 and g = 10 `m//s^(2)`. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
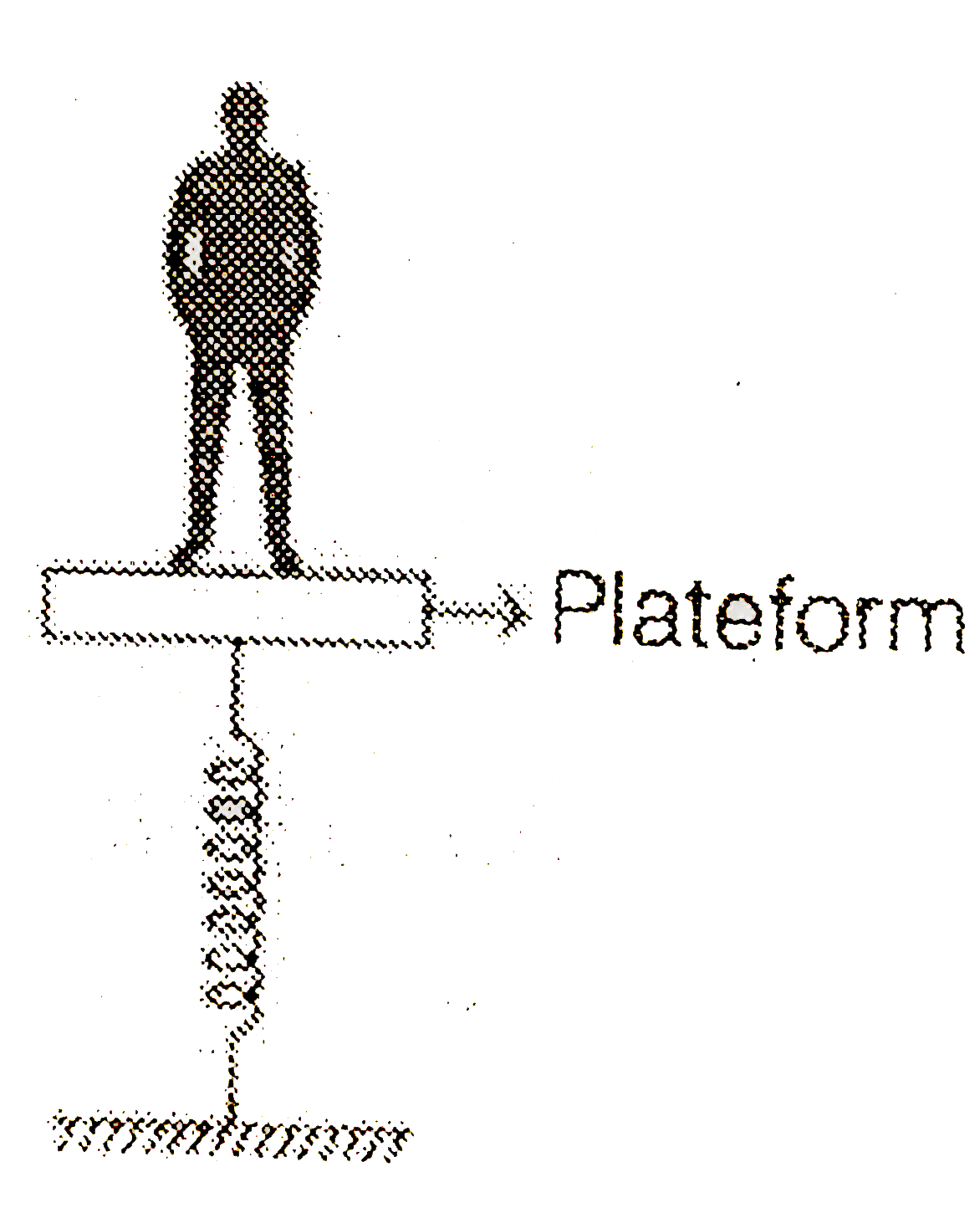
Which of the following will be correct for reading of weighting machine
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density `rho`, density of the material of the cylinder is `3rho`. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
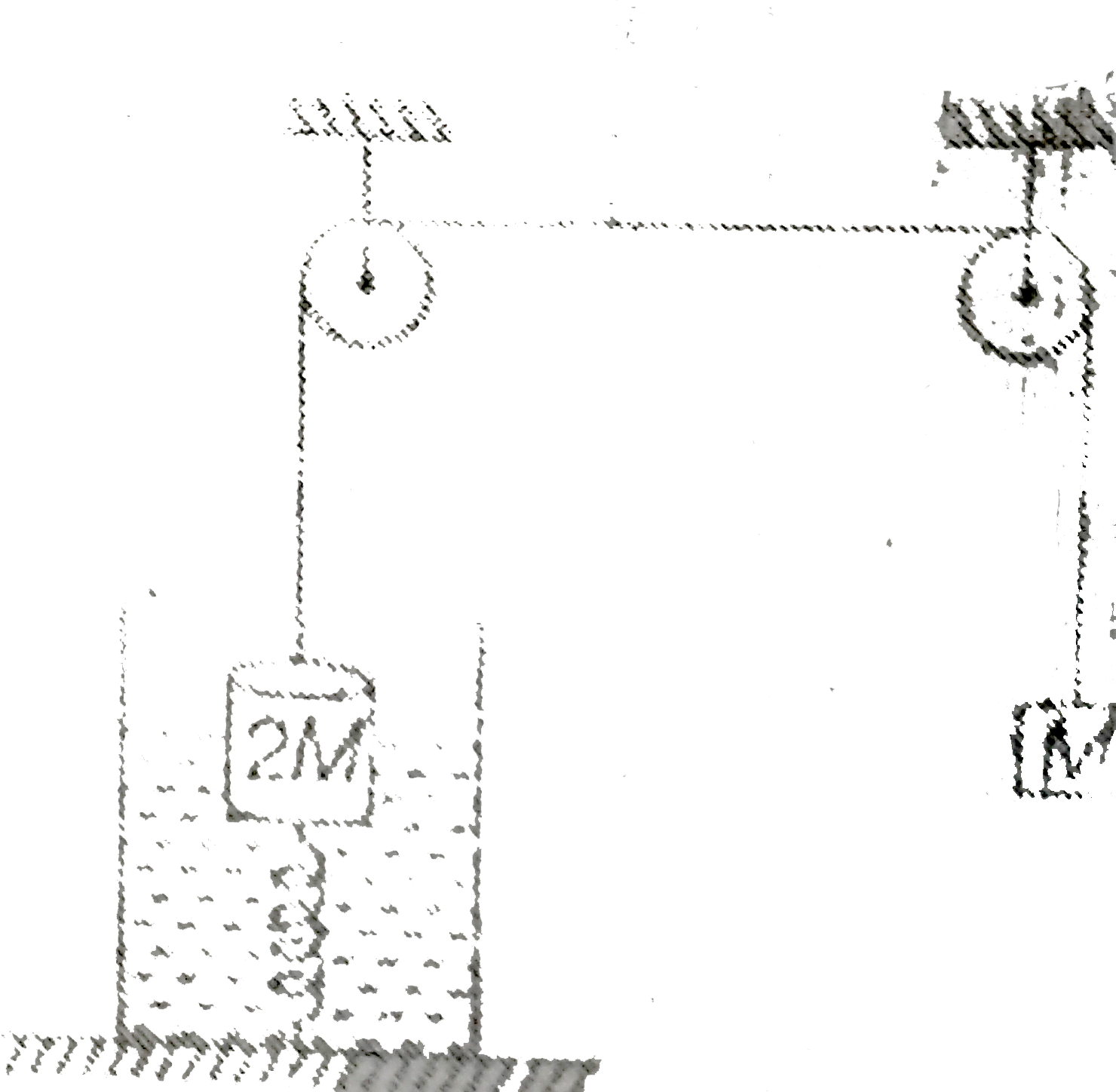
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density `rho`, density of the material of the cylinder is `3rho`. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density `rho`, density of the material of the cylinder is `3rho`. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
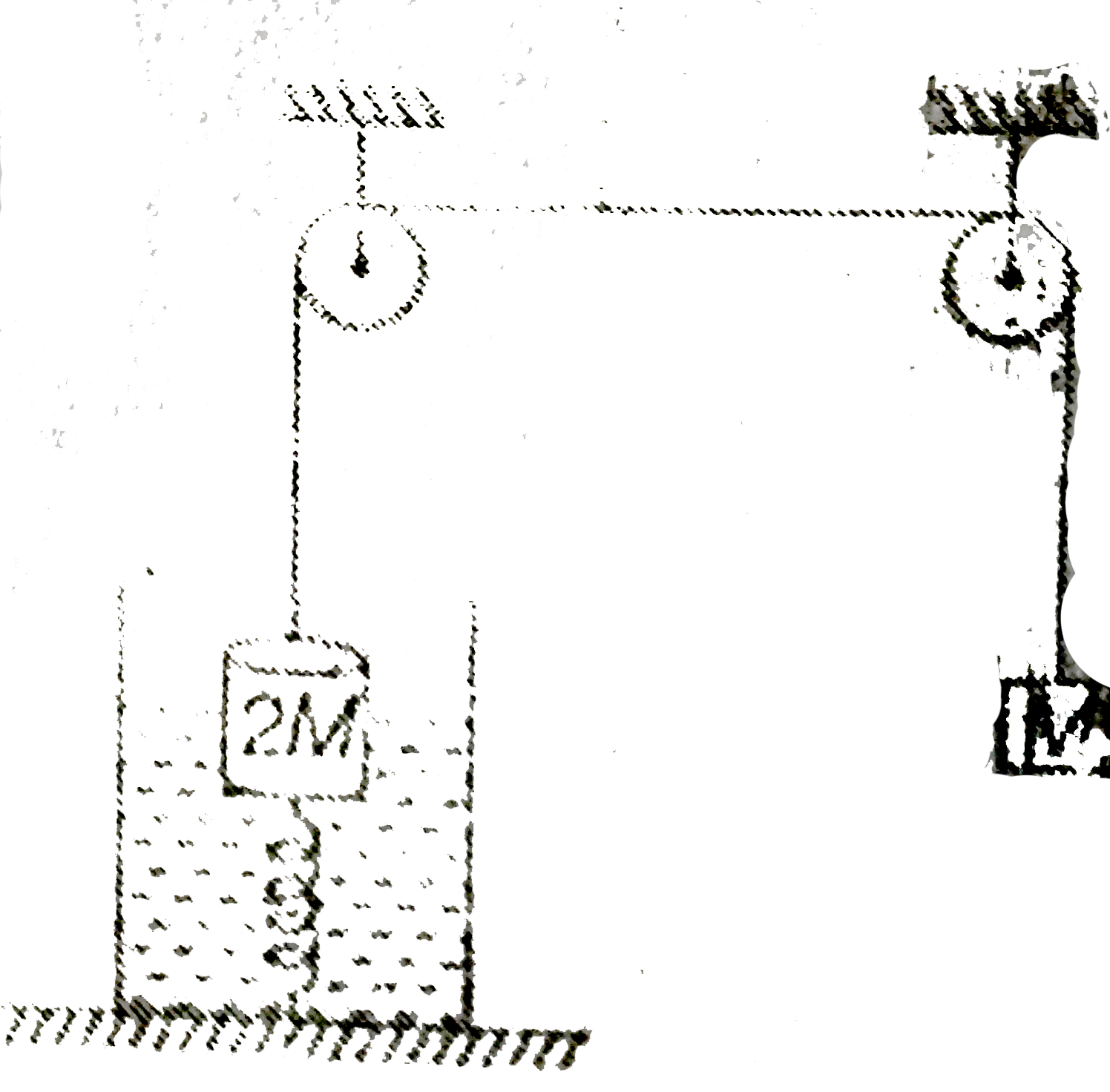
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.
View Solution
More than one option is correct questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct