Complete Solutions to Exercise 14.3 of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Exercise 14.3 |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
`a - x` equation of a body in SHM is `a + 16 x = 0`. Here, `x` is in `cm` and a in `cm//s^(2)`. Find time period of oscillations.
View Solution`A` mass `M`, attached to a spring, oscillates with a period of `2 s`. If the mass is increased by `4kg`, the time period increases by one second. Assuming that Hooke's law is obeyed, find the initial mass `M`.
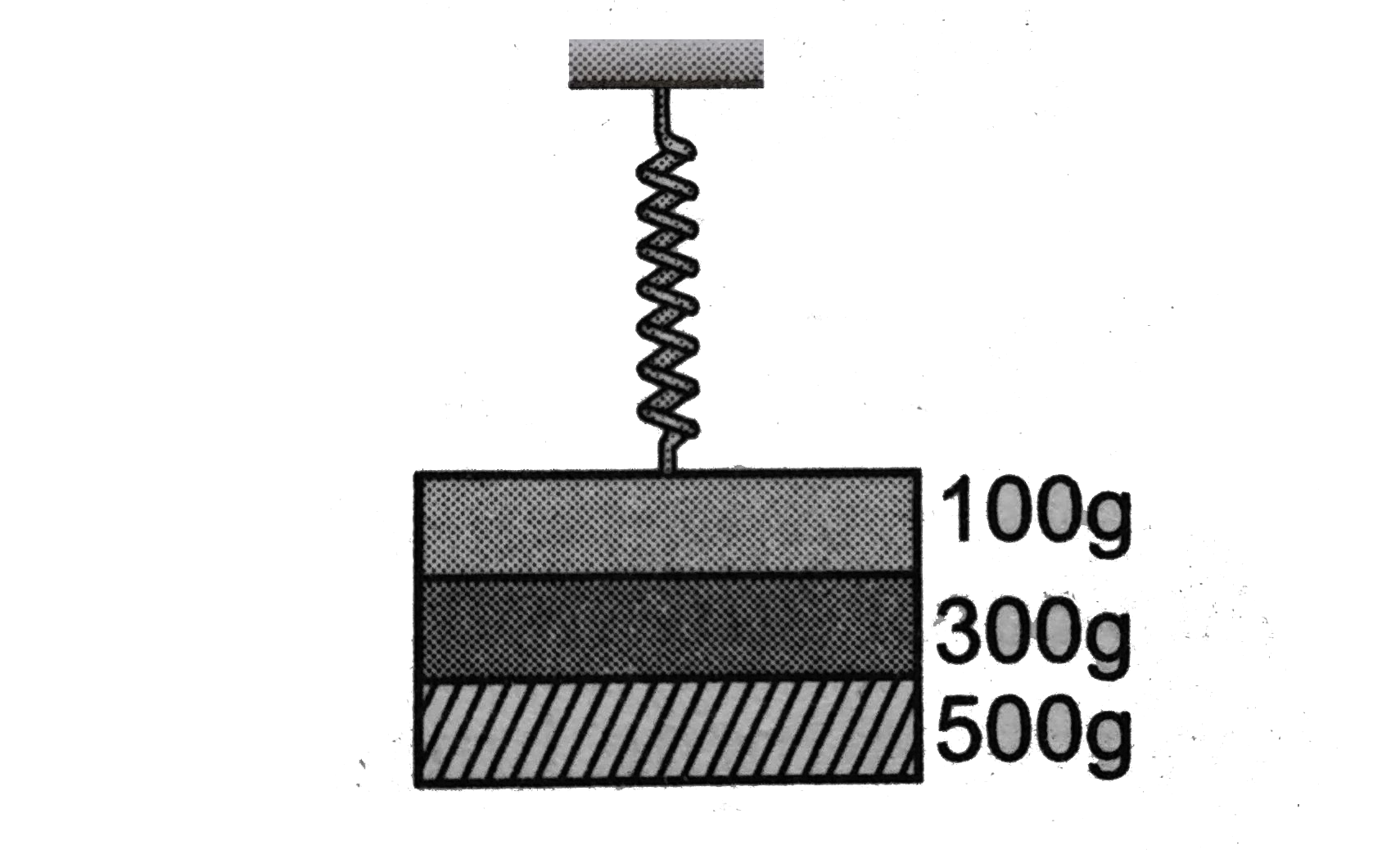
View SolutionThree masses of `500 g`, `300 g` and `100 g` are suspended at the end of a spring as shown and are in equilibrium. When the `500 g` mass is removed suddenly, the system oscillates with a period of `2 s`. When the `300 g` mass is also removed, it will oscillate with period `T`. Find the value of `T`.
View SolutionA particle executes simple harmonic motion. Its instantaneous acceleration is given by `a = - px`, where `p` is a positive constant and `x` is the displacement from the mean position. Find angular frequency of oscillation.
View Solution`A` mass `M` is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period `T`. If the mass is increased by `m`, the time period becomes `(5T)/(3)`. Find the ratio of `m//M`.
View SolutionThe length of a simple pendulum is decreased by `21%`. Find the percentage change in its time period.
View SolutionA particle executes SHM on a straight line path. The amplitude of oscillation is `2cm`. When the displacement of the particle from the mean position is `1cm`, the numerical value of magnitude of acceleration is equal to the mumerical value of velocity. Find the frequency of SHM (in `Hz`).
View Solution
Exercise 14.3 questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct