Complete Solutions to SOLVED EXAMPLES of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| S CHAND | SOLVED EXAMPLES |
| Number Of Questions | 72 |
| Academic Year | 2023-24 |
A race car negotiates a curve of radius 50.0 m on a flat road. What is its angular displacement when it covers a linear distance of 78.5 m?
View SolutionEarth completes one revolution round the sun in 365.25 days. What is the angular velocity ?
View SolutionA satellite moving in a circular orbit at an altitude of 1000 km completes one revolution round the earth in 105 minutes. What is (z) its angular velocity and speed? Radius of the earth `=6.4 xx 10^(6)`m.
View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA pilot of mass 70 kg in a jet aircraft moves in a vertical circle while executing the loop-the-loop at a constant speed of 200 m/s. If the radius of the circle is 2.5 km what is the force exerted by the seat on the pilot at (a) the top of the loop and (b) the bottom of the loop.
View SolutionWhat is the maximum speed with which a cylist can turn around curved path of radius 10.0 m, if the coefficient of friction between the tyre and the road is 0.5 ? If the cyclist wants to avoid overturning by what angle the cyclist must lean from the vertical ?
View SolutionA small toy car moves round a circular track of radius 4 m. The car makes one revolution in 10 s. Calculate (a) the speed of the car, (b) its centripetal acceleration, (c) the centripetal force exerted,by the track if the.mass of the car is 200 g, (d) the safe speed with which the car can move around without toppling, if the distance between the wheels is 4 cm and the height of the centre of gravity of the car from the horizontal is 2 cm.
View SolutionA pick up van negotiates an unbanked curve of radius 40 m with a crate of eggs in the middle of its flat bed. If the coefficient of static friction between the crate and the truck, is 0.55 what is the maximum speed the van can take, so that the crate does not slide ?
View SolutionThe radius of the bump on a road is r. What force does the road exert on a car of mass m when the car passes the highest point on the bump ? Calculate the maximum speed with which the car can pass the highest point before losing contact wtih the road ?
View SolutionAt what angle must a railway track with a level of 300 m radius be banked for safe running of trains at a speed of `90 km h^(-1)` ?
View SolutionA cyclist riding at a speed, of `24.25 ms^(-1)` takes a round a circular road of radius 34.64 m. What is his inclination to the vertical ?
View SolutionAn aeroplane travelling at a speed of 500 km/hr tilts at an angle of 30° as it makes a turn. What is the radius of the curve ?
View SolutionThe distance between the inner and outer wheels of a car is 1.75 m and its centre of gravity is 0-50 m above the ground. What is the maximum speed with which the car can negotiate a curve of radius of 40 m without overturning ?
View SolutionA bend in a level road has a radius of 100 m. What is the maximum speed which a car turning this bend may have without skidding if the coefficient of friction between the road and the tyres in 0.3. If the centripetal force is provided by 'banking' what is the angle of banking?
View SolutionThe bob of a pendulum is released from a horizontal position. If the lenght of the pendulum is 1.5 m what is the speed with which the bob arrives at the lowermost point, given that it dissipated `5%` of its initial energy against air resistance?
View SolutionA small ball `B` of mass `m` is suspended with light inelastic string of length `L` from a block `A` of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle `theta` from equilibrium position and then released.
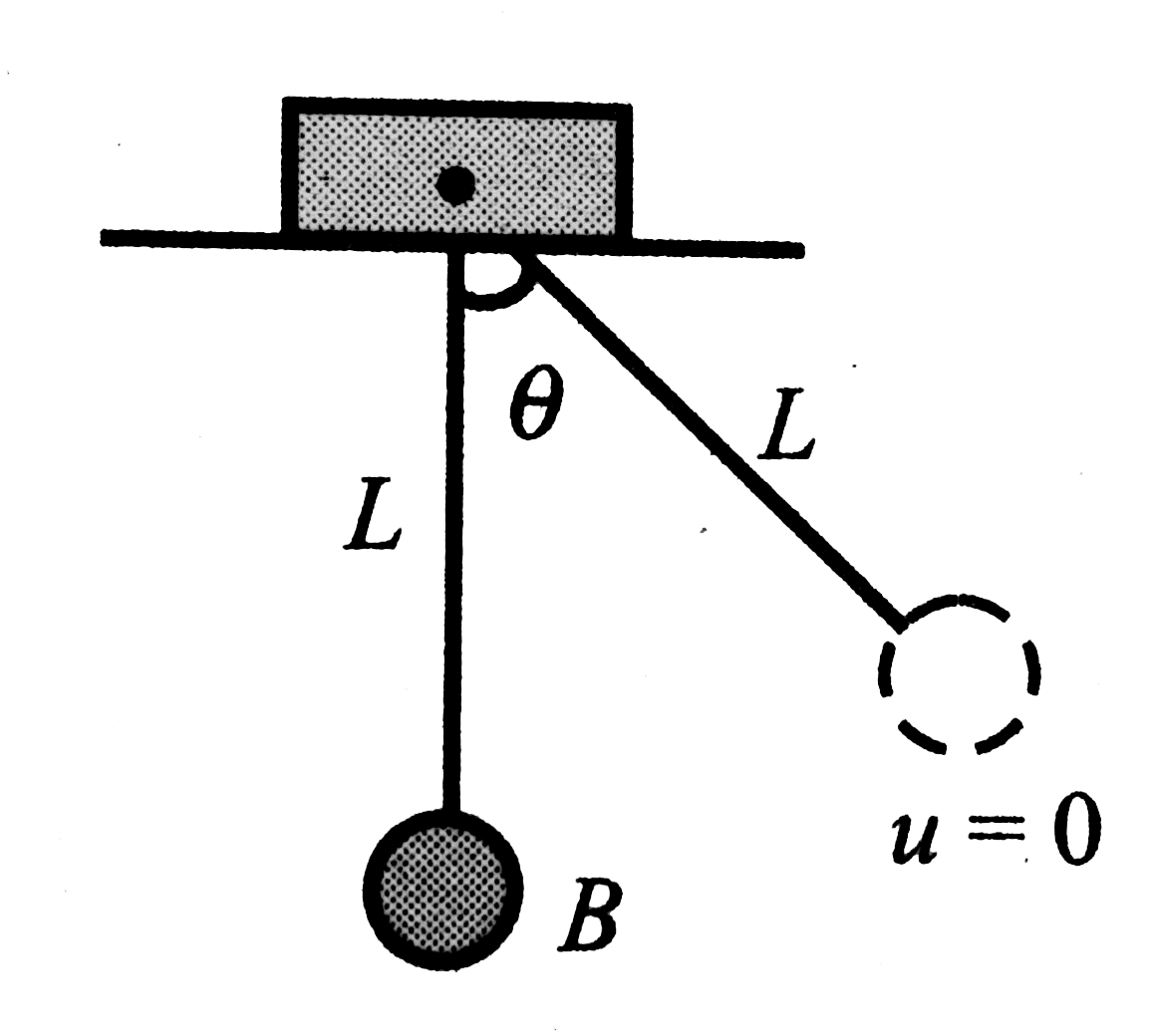 The displacement of centre of mass of `A + B` system till the string becomes vertical is
The displacement of centre of mass of `A + B` system till the string becomes vertical is
View SolutionOne end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA broad gauge train runs at a speed of 72 km/h on a curved track of radius of curvature 1 km. Find the elevation of the outer rail above the inner rail so that there may be side-pressure on the rails ? Distance between the rails is 1.7 m.
View SolutionA cylclist is riding with a speed of `27 km h^-1`. As he approaches a circular turn on the road of radius `80 m`, he applies brakes and reduces his speed at the constant rate of `0.5 ms^-2`. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionA string 1 m long can just support a weight of 16 kg. A mass of 1 kg is attached to one of its ends. The body is revolved in a horizontal circle about the other fixed end of the stringy Find the greatest number of revolutions made by the mass per seconds ? (Take `g=10 ms^(-2)`)
The maximum tension the string can withstand = weight of 16 kg.
View SolutionFig. show a conical pendulum. If the length of the pendulum is `l`, mass of die bob is m and `theta` is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
`L = sqrt((m^(2)gl^(3) sin^(4)theta)/(cos theta))`
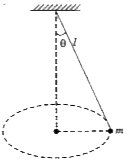
View SolutionFig. show a conical pendulum. If the length of the pendulum is `l`, mass of die bob is m and `theta` is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
`L = sqrt((m^(2)gl^(3) sin^(4)theta)/(cos theta))`

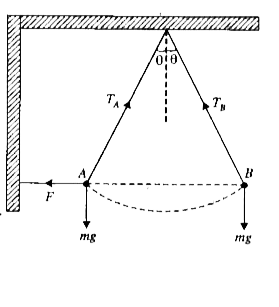
View SolutionUsing two light cords a bob is held in equilibrium at A. The horizontal cord is cut and the bob is allowed to swing as a pendulum. Calculate the ratio of the tension in the supporting cord in position B to that in position A.
View SolutionIn all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
`{:((A) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q01##) "Conical pendulum", (P)T= mg cos theta) ,((B) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q02##)"Pendulum is swinging. Angular position is the extreme position". "T is tension in extreme position", (Q) T cos theta = mg) ,((C) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q03##) "The car is moving with constant acceleration." "The ball is at rest with respect to car",(R) "Speed of ball with respect to ground is constant"),((D) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q04##) "The car is moving with constant velocity"." The ball is at rest with respect to car", (S) "Velocity of ball with respect to ground is changing continuously"):}`
View SolutionA sphere of radius `10 cm` and mass `25` kg is attached to the lower end of a steel wire of length `5 m ` and diameter `4 mm ` which is suspended from the ceiling of a room . The point of support is `521 cm ` above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position `(Y_(steel) = 2xx10^(11) N//m^(2))`.
View SolutionA racing car travelling at `35 ms^(-1)` along a circular path of radius 700 m, starts picking up speed at the rate of `2 ms^(-2)` What is its total acceleration ?
View SolutionWhat is the magnitude and direction of total linears acceleration of a particle moving in a circular path of radius 0.7 m having an instantaneous angular velocity of `3.5 rad s^(-1)` and angular acceleration of `4.2 rad s^(-2)`.
View SolutionThe shaft of a motor rotates at a constant speed of 1800 rpm. What is the angle in radians it has turned through in one second ?
View SolutionThe blades of an aeroplane propeller are 2 m long and rotate at 300 rpm. Calculate (i) the frequency, (ii) period of rotation, (iii) the angular velocity, (iv) linear velocity of point 0.5 m from the top of the blades.
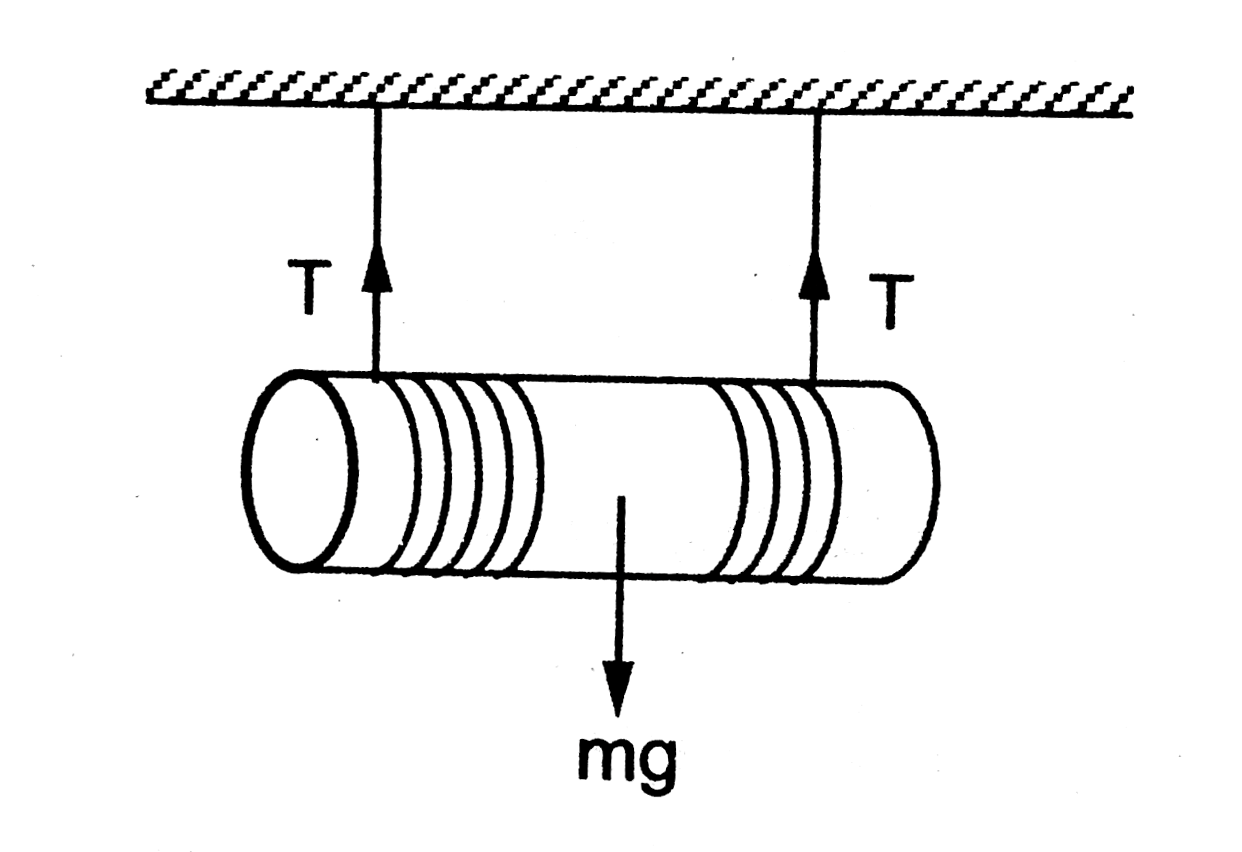
View SolutionA uniform round object of mass `M`, radius `R` and moment of inertia about its centre of mass `I_(cm)` has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take `(I_(cm))/(MR^(2))=k`]
View SolutionA flywheel requires 3 s to rotate through 234 radian. If its angular velocity at 3 s is 108 rad/s, find the initial velocity and uniform acceleration.
View SolutionA flywheel starts rotating from rest when a torque is applied on it, with a uniform angular acceleration of `5 "rad"//s^(2)`. What is the angular displacement of the flywheel in the 5th Second ?
View SolutionA block is released from A on a frictionless track as shown in Fig. 7.2.6. What is the magnitude of radial acceleration and the total acceleration of the block at B ?
View SolutionIn the HCl molecule, the separation between the nuclei of two atoms is about 1.27 A (`1 A = 10^(-10)`m). Find the approximate location of the CM. of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.

View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionTwo particles of masses 100 gm and 300 gm have at a given time, position `2hati + 5hatj + 13hatk` and `-6hati + 4hatj -2hatk` respectively and velocities `10hati - 7hatj - 3hatk` and `-7hati - 9hatj - 6hatk` m/s respectively. Deduce the instantaneous position and velocity of the Centre of mass.
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is `(g = 10 m/s^2)`
View SolutionThe distance between the two atoms in a diatomic molecule `O_(2)` is `1.21 xx 10^(-10)` m. The mass of each oxygen atom is `2.66 xx 10^(-26)` kg. Treating the atoms as point masses find the m moment of inertia of the molecule about an axis passing perpendicular to the line joining the centres of the atoms.
View SolutionThe mass of a disc is 700 gm and its radius of gyration is 20 cm. What is its moment of inertia if it rotates about an axis passing through its centre and perpendicular to the face of the disc?
View SolutionA cross-section of a solid cylinder is shown in Fig. 7.2.20, with the core section protruding from the larger drum. A rope wrapped around the drum of radius `r_(1) = 80` cm exerts a force 10.0 N to the right on the cylinder. The cylinder can rotate freely around the central axis. A rope wrapped around the core of radius `r_2 = 40 cm` exerts a force of 15.0 N downwards on the cylinder, (a) Calculate the net torque acting on the cylinder about the axis of rotation ?
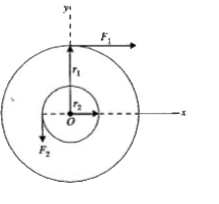
View SolutionA particle of mass 50 gm moving in a circle at 5 cm radius with a constant speed of 10 cm/s. What is its angular momentum about (i) centre of the circle, (ii) a point on the axis of the circle at 4 cm distance from its centre ? Which of these will be always in the same direction ? [Fig.]
View SolutionA bob of mass 200 gm is attached to a string of length 100 cm and is revolved at the rate of 2 revolutions per second. What is its angular momentum ? If after 10 s it makes only on revolutions per second calculate the mean torque.
View SolutionA torque of 10 Nm is applied to a flywheel of mass 5 kg and radius of gyration 0.6 m. What is the resultant angular acceleration ?
View SolutionThe earth is rotating with an angular velocity of `7.3 xx 10^(-5)` rad/s. What is the tangential force needed to stop the earth in one year ? Given moment of inertia of the earth about the axis of rotation = `9.3 xx 10^(37) m^(2)`. Radius of the earth = `6.4 xx 10^(6)` m
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View SolutionIn all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
`{:((A) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q01##) "Conical pendulum", (P)T= mg cos theta) ,((B) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q02##)"Pendulum is swinging. Angular position is the extreme position". "T is tension in extreme position", (Q) T cos theta = mg) ,((C) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q03##) "The car is moving with constant acceleration." "The ball is at rest with respect to car",(R) "Speed of ball with respect to ground is constant"),((D) (##VMC_PHY_XI_WOR_BOK_01_C04_E03_050_Q04##) "The car is moving with constant velocity"." The ball is at rest with respect to car", (S) "Velocity of ball with respect to ground is changing continuously"):}`
View SolutionA flywheel of mass 100 kg and radius 1 m is rotating at the rate of 420 rev/min. Find the constant retarding torque to stop the wheel in 14 revolutions, the mass is concentrated at the rim. M.I. of the flywheel about its axis of rotation `I = mr^(2)`.
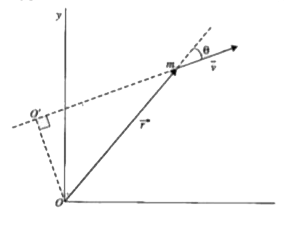
View SolutionA point mass 10 g moves in the xy plane with a velocity `2 ms^(-1)` along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector `vecr` is 0.5 m and the angle `theta = 30^(@)`.
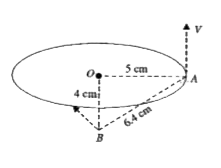
View SolutionA particle is tied to the end of a string of length 20 cm and makes 5 rps. How many revolutions will it make in one second when the string is shortened to 10 cm ?
View SolutionA horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
View SolutionA circular disc of 49 kg and radius 50 cm is rotating at a speed of 120 rotations per minute. Calculate its kinetic energy if is moment of inertia about the axis of rotation is `1/2 mr^(2)`.
View SolutionA sphere of mass 50 gm and diameter 2 cm rolls without slipping with a velocfty of 5 cm/s. Calculate the total energy.
View SolutionCalculate the work done in increasing the angular velocity of a wheel of moment of inertia 200 kg `m_2` from 20 rev/s to 40 rev/s.
View SolutionThe flywheel of an engine, acted upon by a constant torque at the rate of 3000 rev/ min and develops a power of 10 kW. Find the torque acting on the wheel.
View SolutionThe rotational kinetic energy of a disc is 450 J and its moment of inertia is 100 kg `m^2`. What is its angular momentum ?
View SolutionOne end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.
View SolutionCalculate'the final speed acquired by the softd cylinder shown in Fig.2.48 when it rolls down and reaches the bottom of the inclined plane' without slipping. Assume that the inclined plane is frictionless.
View SolutionA solid sphere of radius `2.45m` is rotating with an angular speed of `10 rad//s`. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA thin meter scale is kept vertical by placing its one end on floor, keeping the end in contact stationary, it is allowed to fall. Calculate the velocity of its upper end when it hit the floor.
View SolutionA rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. If the rope is pulled with a force of 30 N, then the angular acceleration produced in the cylinder is
View SolutionA flywheel of mass 140 kg and radius of gyration 3.5 m is rotated with a speed of 240 rpm. Find the torque required to stop it in 3.5 rotations ?
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
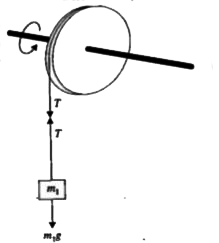
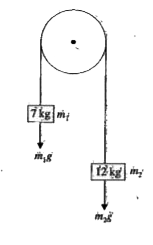
View SolutionIn the Atwood's machine shown in Fig. `m_1 = 7` kg and `m_2 = 12` kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley of radius 5 cm. When the system is released from rest the heavier mass is found to fall 1 m in 2 s. Calculate the moment of inertia of the pulley ?
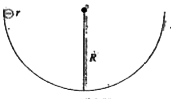
View SolutionThe radius of a large hemisphere whose" axis of symmetry is vertical is R = 50 cm. A small sphere of radius r= 5cm rolls without slipping with a speed of 2cm/s. The mass of the sphere is 100 gm. If it start's at the top from rest (i) what is the kinetic energy at the bottom? (ii) What fraction is rotational ? (iii) What fraction is translational?
View SolutionThe mass of a spool of wire in the form of a uniform solid cylinder is m and its radius is r. The wire is unwound under a constant force F. Assume that the cylinder does not slip, find (i) the acceleration of the centre of mass, (ii) the force of friction, (iii) what is the speed attained by the centre of mass after the cylinder has rolled through a distance, assume that the cylinder starts from rest and it rolls without slipping ?
View SolutionA uniform thin rod of mass `m` and length `l` is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle `theta` with horizontal.
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
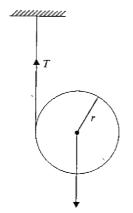
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find (a). the tension T in the string and (b). the speed o the cylinder as it falls through a distance h.
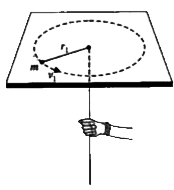
View SolutionA mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity `v_(1)` in a circle of radius `r_(1)` The string is then slowly pulled from below, decreasing the radius of the circles to `r_2` (i) What is the speed of the mass when the radius is `r_2` ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from `r_(1)` to `r_(2)`?
View SolutionDerive an expression for the moment of inertia of a thin spherical shell about a diameter.
View SolutionDerive an expression for the moment of inertia of a thin spherical shell about a diameter.
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter CIRCULAR MOTION of S CHAND PHYSICS (ENGLISH) of Class 11
All Exercises from S CHAND Class 11 PHYSICS CIRCULAR MOTION
- MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
- MODULE 1 (FROM ANGULAR VELOCITY)
- MODULE 1 (FROM BANKING OR RAILS AND ROADS)
- MODULE 1 (FROM CENTRIPETAL FORCE)
- MODULE 1 (LONG ANSWER QUESTIONS)
- MODULE 1 (SHORT ANSWER QUESTIONS)
- MODULE 1 (VERY SHORT ANSWER QUESTIONS)
- MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
- MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)
- MODULE 2 (FROM CENTRE OF MASS)
- MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
- MODULE 2 (FROM MOMENT OF INERTIA, TORQUE)
- MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
- MODULE 2 (LONG ANSWER QUESTIONS)
- MODULE 2 (SHORT ANSWER QUESTIONS)
- MODULE 2 (VERY SHORT ANSWER QUESTIONS)
- SOLVED EXAMPLES