Complete Solutions to Level-III of chapter SYSTEM OF PARTICLES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES |
| NARAYANA | Level-III |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
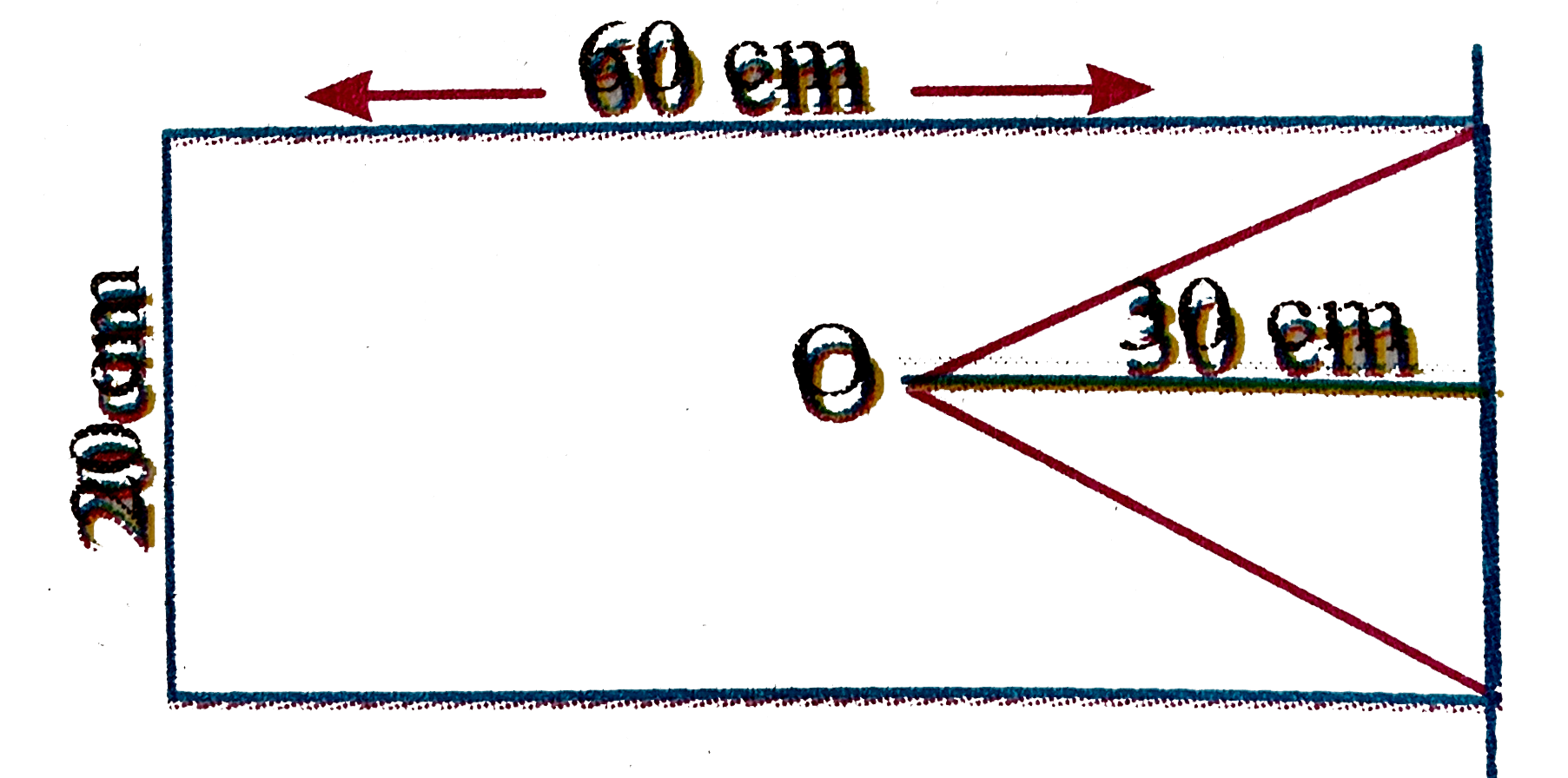
Seven homogeneous bricks, each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by `L/10`. Find the x-coordinate of the centre of mass relative to the origin shown.

View SolutionThe centre of mass of a non uniform rod of length L, whose mass per unit length varies as `rho=(k.x^2)/(L)` where k is a constant and x is the distance of any point from one end is (from the same end)
View SolutionA rope of length `30cm` is on a horizontal table with maximum length hanging from edge `A` of the table. The coefficient of friction between the rope and table is `0.5`. The distance of centre of mass of the rope from `A` is
View SolutionAs shown in figure from a uniform rectangular sheet a triangular sheet is removed from one edge. The shift of centre of mass is
View SolutionA circular disc of radius `R` is removed from a bigger circular disc of radius `2 R` such that the circumferences of the discs coincide. The center of mass of new disc is `alpha R` from the center of the bigger disc. The value of `alpha` is
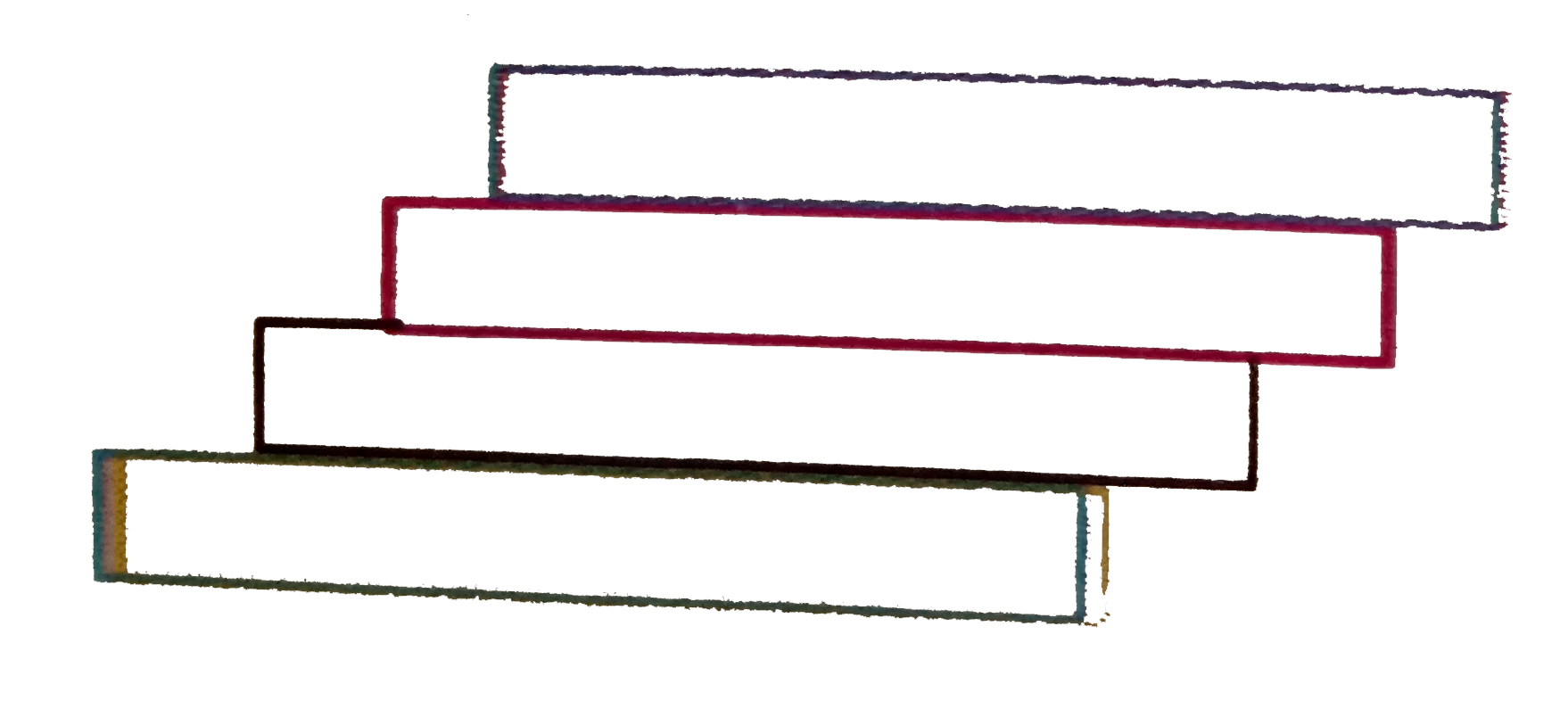
View SolutionIdentical blocks each of mass `M` and length `L` are placed one above the other such that each extends out by a maximum length as shown in figure. Find the maximum extension of the `n^(th)` block from the top, so that the blocks will not fall.
View SolutionTwo bodies with masses `m_1` and `m_2(m_1gtm_2)` are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system `(m_1+m_2)` is
View SolutionTwo bodies of masses `m_1` and `m_2` are moving with velocity `v_1` and `v_2` respectively in the same direction. The total momentum of the system in the frame of reference attached to the centre of mass is (`v` is relative velocity between the masses)
View SolutionA shell in flight explodes into `n` equal fragments `k` of the fragments reach the ground earlier than the other fragments. The acceleration of their centre of mass subsequently will be
View SolutionA body of mass `m` is dropped and another body of mass `M` is projected vertically up with speed `u` simultaneously from the top of a tower of height `H`. If the body reaches the highest piont before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionA rope thrown over a pulley has a ladder with a man of mass `m` on one of its ends and a counter balancing mass `M` on its other end. The man climbs with a velocity `v_r` relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionTwo particles of masses `2kg` and `3kg` are projected horizontally in opposite directions from the top of a tower of height `39.2m` with velocities `5m//s` and `10m//s` respectively. The horizontal range of the centre of mass of two particles is
View SolutionTwo particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds `u_A=200m//s` and `u_B=50m//s`. Initially they were `90m` apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
`(g=10m//s^2)`

View SolutionAt a given instant of time the position vector of a particle moving in a circle with a velocity `3hat i - 4 hat j + 5 hat k` is `hat i + 9 hat j - 8 hat k`. Its angular velocity at that time is:
View Solution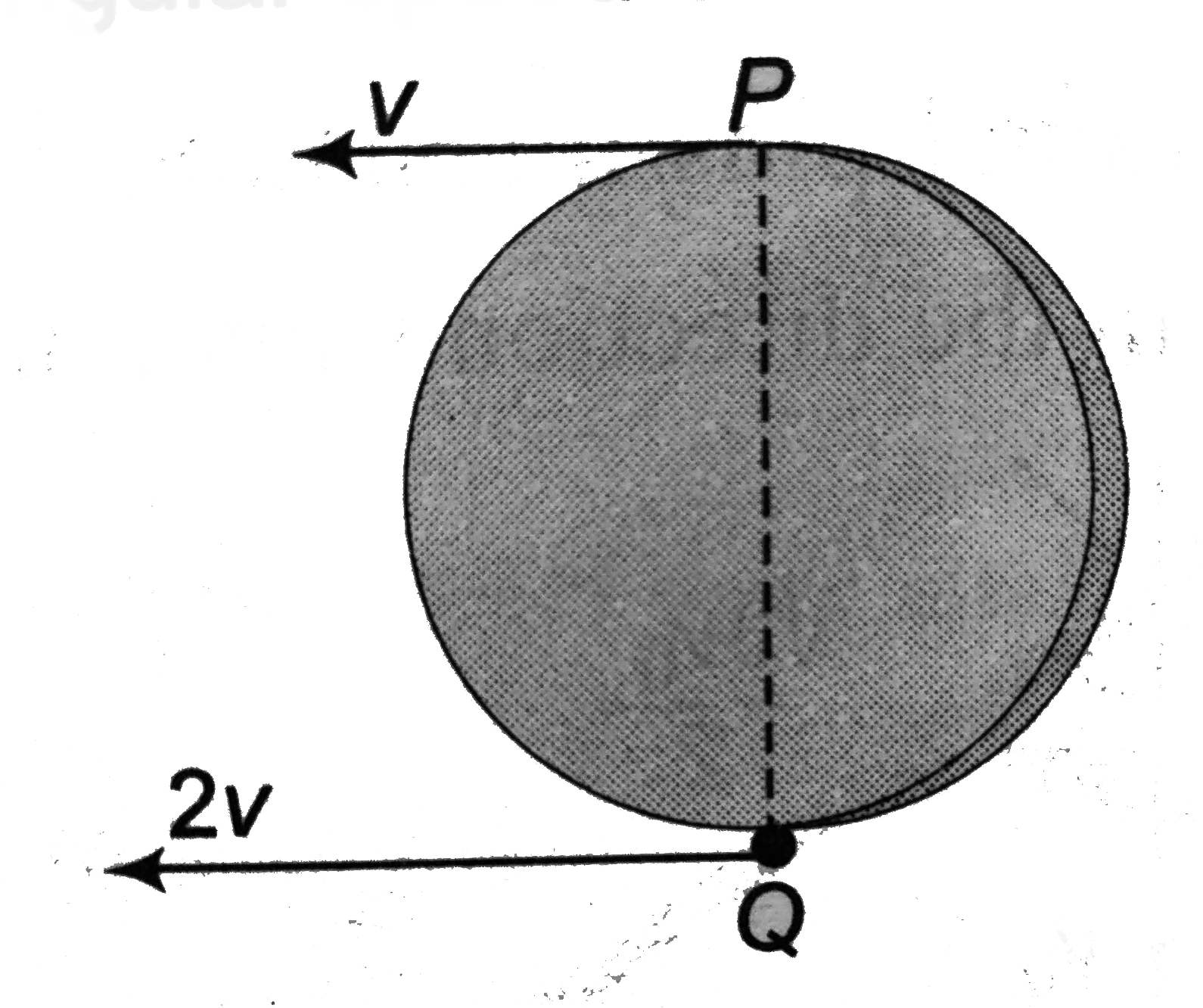
Two point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
View SolutionPoint `A` of rod `AB(l=2m)` is moved upwards against a wall with velocity `v=2m//s`. Find angular speed of the rod at an instant when `theta =60^@.`

View SolutionA uniform circular disc of radius `R` lies in the `XY` plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance `x=2R` and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a point on the Y-axis at a distance `y=d` and parallel to the X-axis in the X-Y plane. The value of `d` is
View SolutionA wheel rotating with uniform angular acceleration covers 50 revolutions in the first five seconds after the start. Find the angular acceleration and the angular velocity at the end of five seconds.
View Solution
A square is made by joining four rods each of mass `M` and length `L`. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is
View SolutionA shaft is turning at `65rad//s` at time zero. Thereafter, angular acceleration is given by `alpha=-10rad//s^(2)-5trad//s^(2)`
Where `t` is the elapsed time
(a). Find its angular speed at `t=3.0` s
(b). How much angle does it turn in these `3s`?
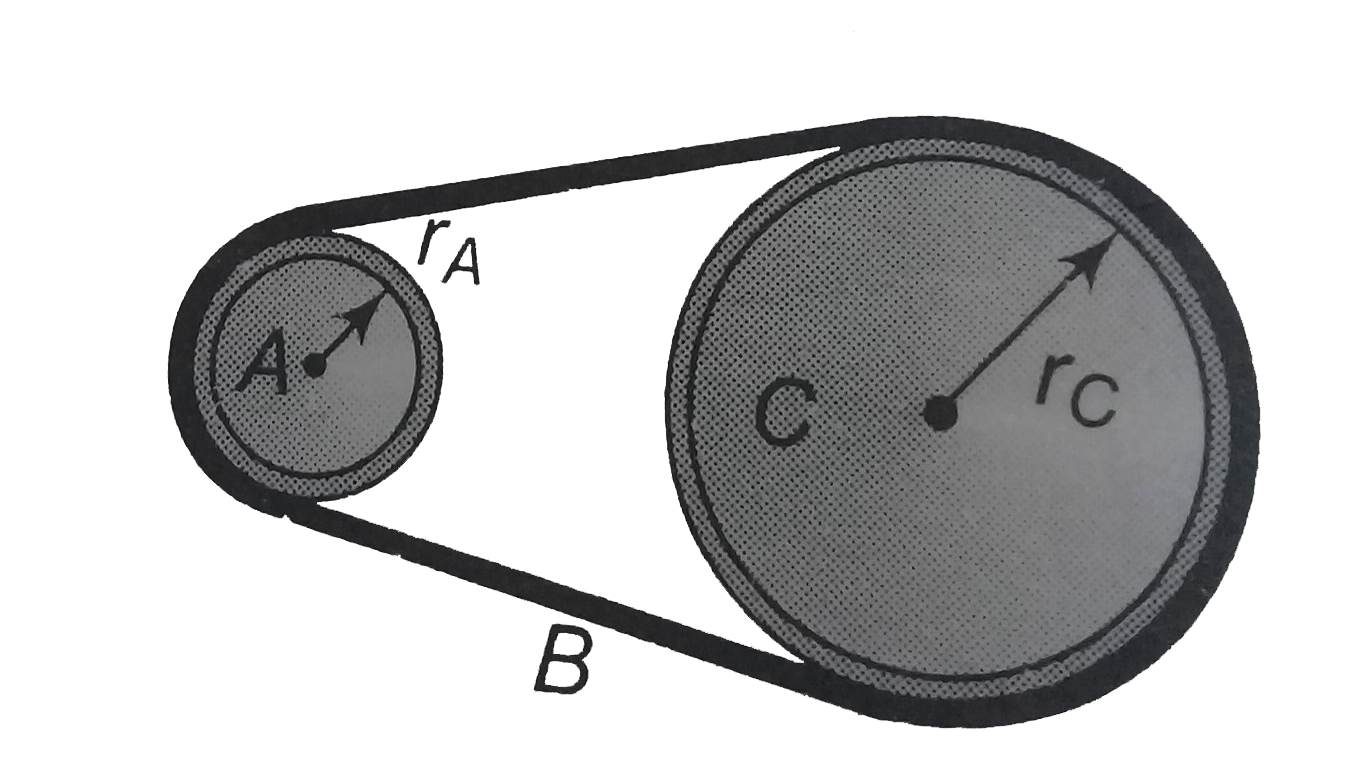
View SolutionIn figure wheel `A` of radius `r_A = 10 cm` is coupled by belt `B` to wheel `C` of radius `r_C = 25 cm`. The angular speed of wheel `A` is increased from rest at a constant rate of `1.6 rad//s^2`. Find the time needed for wheel `C` to reach an angular speed of `12.8 rad//s`, assuming the belt does not slip.
 .
.
View SolutionAn equilateral prism of mass `m` rests on a rough horizontal surface with coefficient of friction `mu`. A horizontal force `F` is applied on the prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is

View SolutionThe mass of a metallic beam of uniform thickness and of length `6m` is `60kg`. The beam is horizontally and symmetrically lies on two vertical pillars which are separated by a distance `3m`. A person of mass `75kg` is walking on this beam. The closest distance to which the person can approach one end of the beam so that the beam does not tilt down is (neglect thickness of pillars)
View SolutionTwo persons `P` and `Q` of same height are carrying a uniform beam of length `3m`. If `Q` is at end, the distane of `P` from the other end so that `P,Q` receive loads in the ratio `5:3` is
View SolutionA uniform meter scale of mass `1kg` is placed on table such that a part of the scale is beyond the edge. If a body of mass `0.25kg` is hung at the end of the scale then the minimum length of scale that sould lie on the table so that it does not tilt is
View SolutionA metallic cube of side length `1.5m` and of mass `3.2` metric ton is on horizontal rough sloor. The minimum horizontal force that should be applied on the cube at a height `1.2m` from that floor to turn the cube about its lower edge is
View SolutionA cubical block of side `L` rests on a rough horizontal surface with coefficient of friction `mu`. A horizontal force `F` is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 .
.
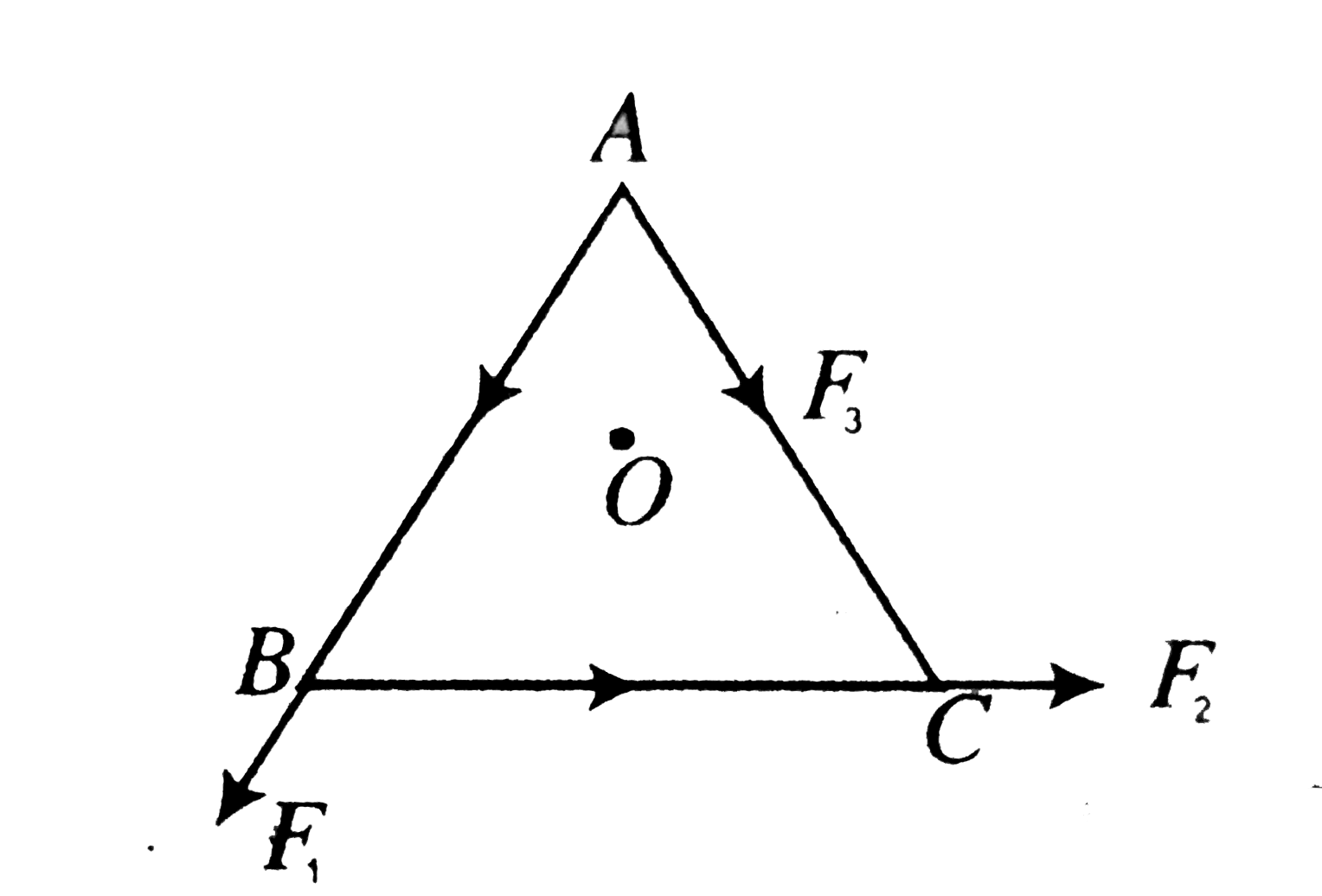
View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
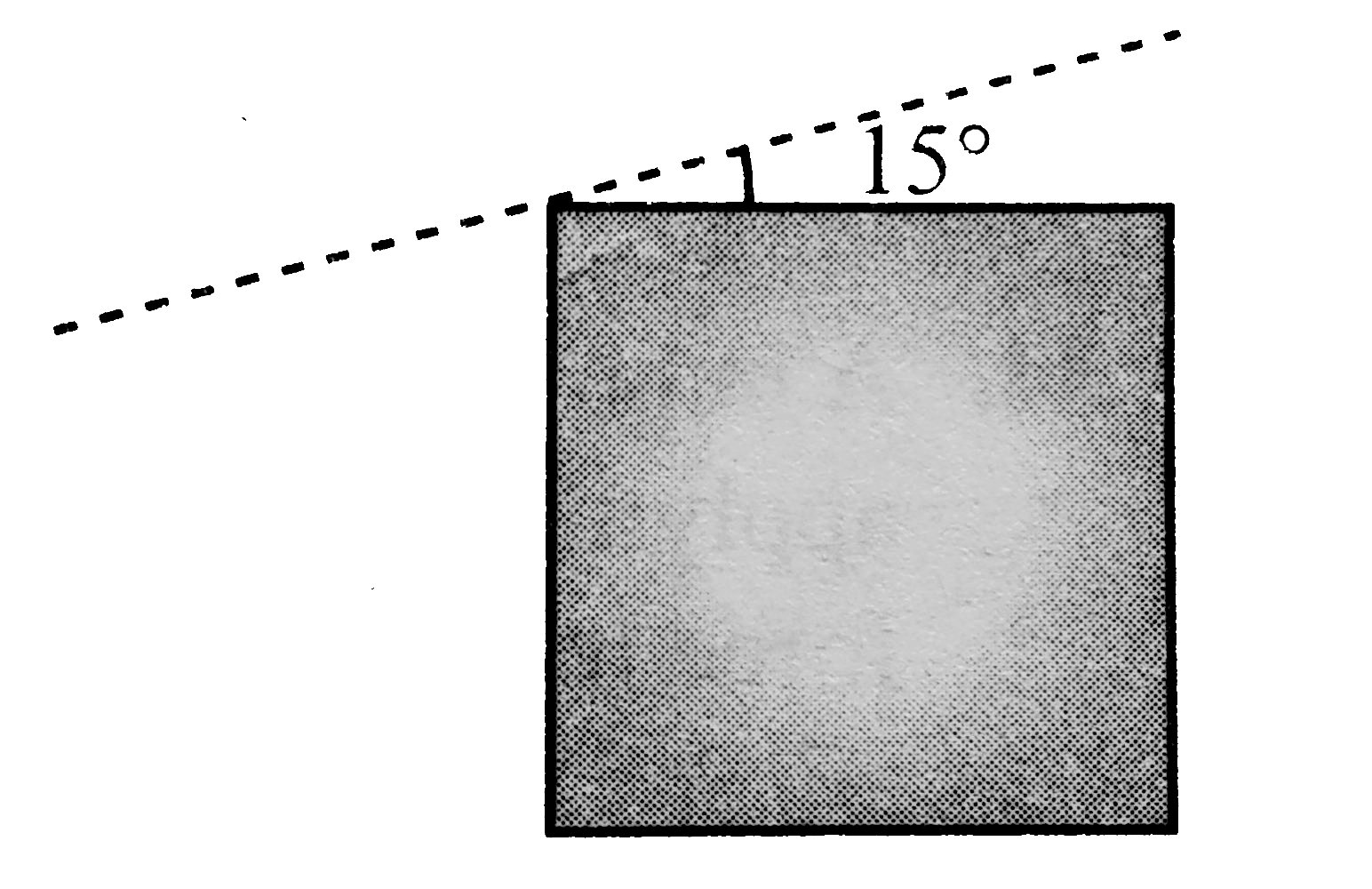
View SolutionA square plate of mass `M` and edge `L` is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle `15^@` horizontal is `
View SolutionA thin rod of length `L` of mass `M` is bent at the middle point `O` at an angle of `60^@`. The moment of inertia of the rod about an axis passing through `O` and perpendicular to the plane of the rod will be

View SolutionFour identical solid spheres each of mass `M` and radius `R` are fixed at four corners of a light square frame of side length `4R` such that centres of spheres coincides with corners of square. The moment of inertia of `4` spheres about an axis perpendicular to the plane to frame and passing through its centre is
View SolutionFour identical solid spheres each of mass `M` and radius `R` are fixed at four corners of a light square frame of side length `4R` such that centres of spheres coincides with corners of square, moment of inertia of `4` spheres about an axis passing through any side of square is
View SolutionThickness of a wooden circular plate is same as the thickness of a metal circular plate but density of metal plate is `8` times density of wooden plate. If moment of inertia of wooden plate is twice the moment of inertia of metal plate about their natural axes, then the ratio of radii of wooden plate to metal plate is
View SolutionA uniform circular disc of radius `R` lies in the `XY` plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance `x=2R` and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a pint on the Y-axis at a distance `y=d` and parallel to the X-axis in the X-Y plane. The value of `d` is
View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
View SolutionTwo rings of the same radius `R` and `M` are placed such that their centres coincide and their planes are perpendicular to each other, the moment of inertia of the system about an axis passing through the diameters of both rings is
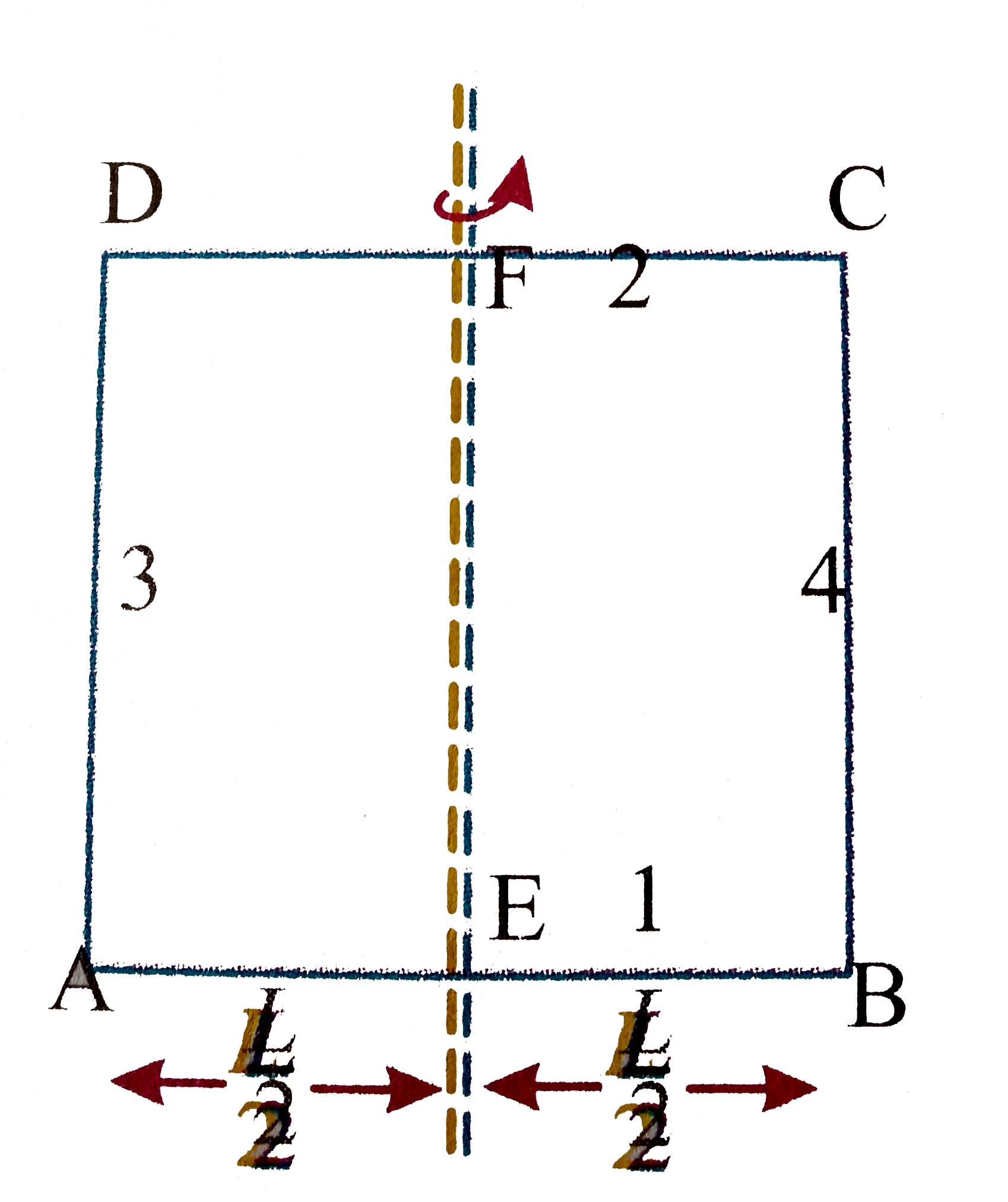
View SolutionFour thin metal rods, each of mass `M` and length `L`, are welded to form a square `ABCD` as shown in figure. The moment of inertia of composite structure about a line which bisects rods `AB` and `CD` is
View SolutionTwo circular loops `A` and `B` are made of the same wire and their radii are in the ratio `1:n`. Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio `1:m`. The relation between `m` and `n` is
View SolutionThe moment of inertia of a hollow sphere of mass `M` having internal and external radii `R` and `2R` about an axis passing through its centre and perpendicular to its plane is
View SolutionFind moment of inertia of half disc of radius `R_2` and mass `M` about its centre. A smaller half disc of radius `R_1` is cut from this disc

View SolutionA uniform smooth rod (mass `m` and length `l`) placed on a smooth horizontal floor is it by a particle (mass `m`) moving on the floor, at a distance `l/4` from one end elastically `(e = 1)`. The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
View SolutionA bullet of mass `m` is fired upward in a direction of angle of projection `60^@` with an initial velocity `u`. The angular momentum of this vullet when it is crossing highest point with respect to point of projection is
View SolutionA particle of mass `5g` is moving with a uniform speed of `3sqrt2 cm//s` in the `x-y` plane along the line `y=x+4`. The magnitude of its angular momentum about the origin in `g cm^(2)//s` is
View SolutionA ballot dancer is rotating about hyis own vertical axis on smooth horizontal floor with a time period `0.5 sec`. The dancer flods himself close to his axis of rotation due to which his radius of gyration decreases by `20%`, then his new time period is
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity `omega_0` about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA uniform circular disc of mass `M` and radius `R` rolls without slipping on a horizontal surface. If the velocity of its centre is `v_0`, then the total angular momentum of the disc about a fixed point `P` at a height `(3R)//2` above the centre `C`.

View SolutionA disc of mass `m` and radius `R` moves in the `x-y` plane as shown in Fig. The angular momentum of the disc about the origin `O` at the instant shown is

View SolutionA uniform sphere of mass `m` radius `r` and moment of inertia `I` about its centre moves along the `x`-axis as shown in Fig. Its centre of mass moves with velocity `= v_(0)`, and it rotates about its centre of mass with angular velocity `=omega_(0)`. Let `vecL=(Iomega_(0)+mv_(0)r)(-k)`. The angular momentum of the body about the origin `O` is

View SolutionIn the figure shown, a ring `A` is initially rolling without sliding with a velocity `1`, on the horizontal surface of the body `B` (of same mass as `A`). All surfaces arc smooth. `B` has no initial velocity. What will be the maximum height reached by `A` on `B`?

View SolutionIn figure calculate the linear acceleration of the blocks.
Mass of block A = 10 kg. Mass of block `B= 8kg`
mass of disc shaped pulley `=2kg`. (take `g=10m//s^(2)`)
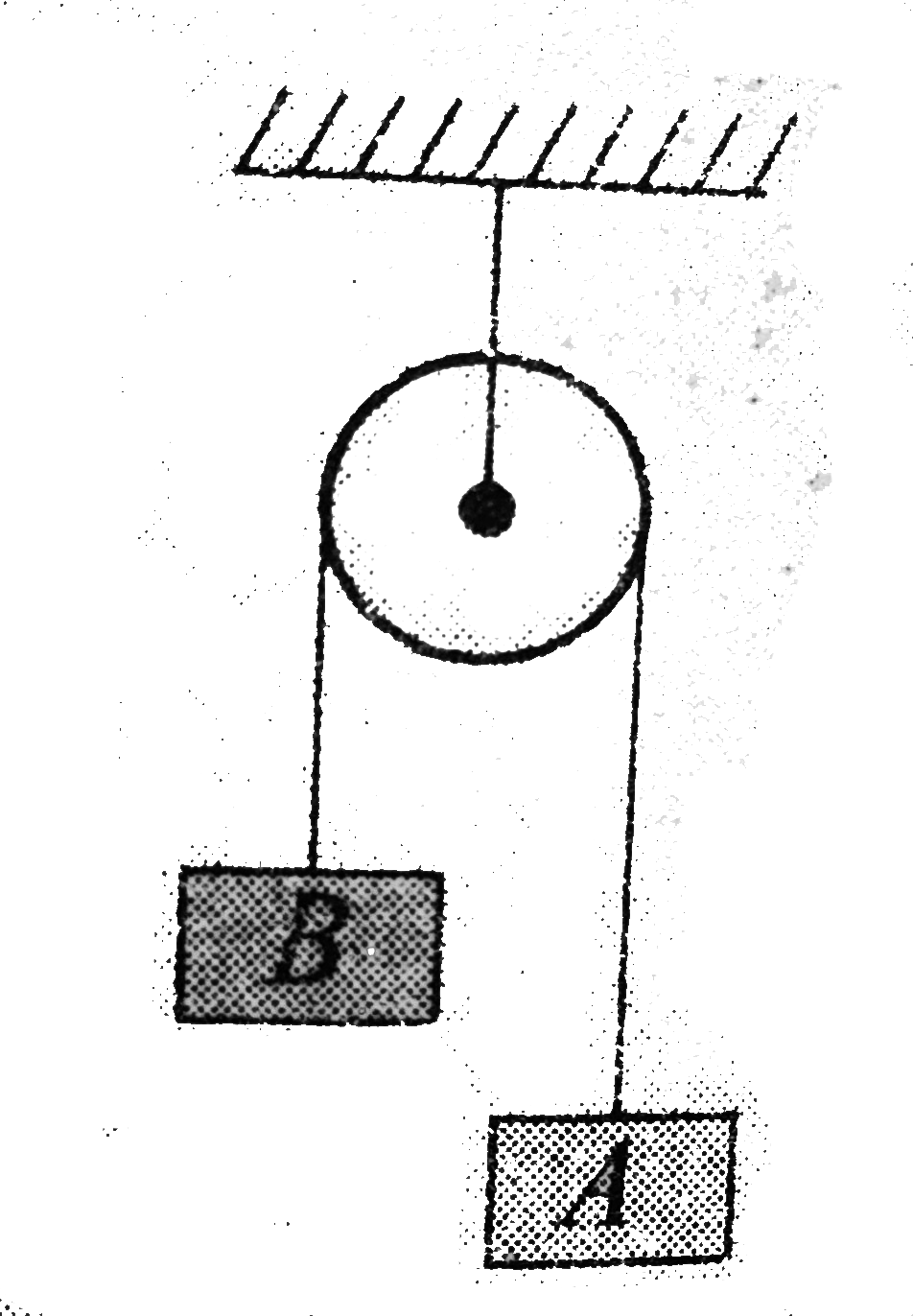
View SolutionA block of mass `m` is attached at the end of an inextensible string which is wound over a rough pulley of mass `M` and radius `R` figure a. Assume the stirng does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA uniform rod of length `L` and mass `M` is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle `theta` with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View SolutionThe arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass `m`, on which two light theads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

View SolutionThe top is figure has moment of inertia equal to `4.00xx10^(-4) kgm^(2)` and is initially at rest. It is free to rotate about the stationary axis `"AA"'`. A string wrapped around a ped alonng the axis of the top is pulled in such a manners as to maintain a constant tension of `5.57N`.If the string does not slip while it is unwound from the peg, what is the angular speed of the top after `80.0 CM` of string has been pulled of the peg?

View SolutionA solid cylinder of mass `m=4kg` and radius `R=10cm` has two ropes wrapped around it, one near each end. The cylinder is held horizontally by fixing the two free ends of he cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the tension along the strings.
View SolutionAssume the earth's orbit around the sun as circular and the distance between their centres as `D` Mass of the earth is `M` and its radius is `R` if earth has an angular velocity `omega_0` with respect to its centre and `omega` with respect to the centre of the sun, the total kinetic energy of the earth is:
View SolutionA cylinder of mass `10 kg` is rolling perfectly on a plane of inclination `30^(@)`. Find the force of friction between the cylinder and the surface of inclined plane.
View SolutionIn Fig. the velocities are in ground frame and the cylinder is performing pure rolling on the plank, velocity of point `'A'` would be
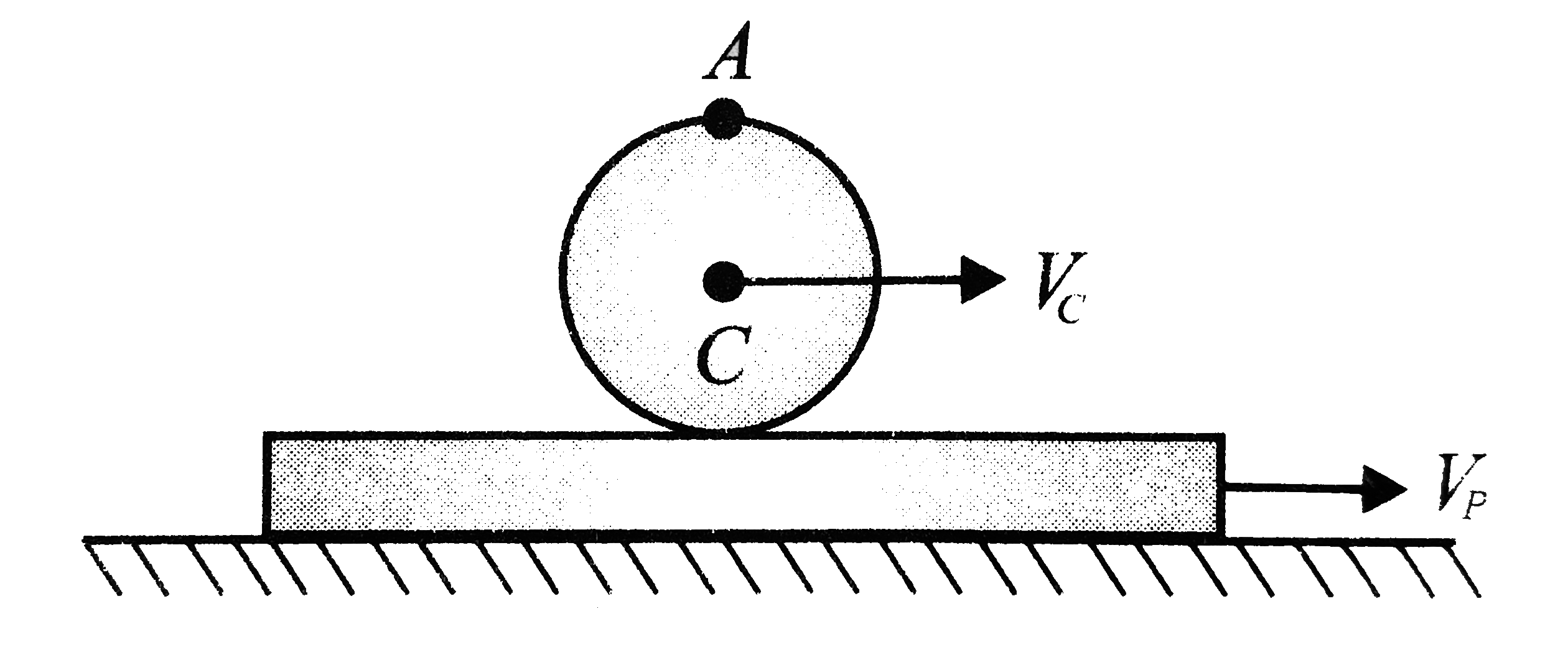
View SolutionA carpet of mass `M` is rolled along its length so as to from a cylinder of radius `R` and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to `R//2`.
View Solution
A tangential force `F` acts at the top of a thin spherical shell of mass `m` and radius `R`. Find the acceleration of the shell if it rolls without slipping.
View SolutionA uniform circular ring of radius `R` is first rotated about its horizontal axis with an angular velocity `omega_0` and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings `mu`. Time after which its angular speed is reduced to `0.5 omega_0` is

View SolutionA disc of radius `R` rolls without slipping at speed `v` along positive `x`-axis. Velocity of point `P` at the instant shown in Fig. is

View SolutionA uniform solid sphere of radius `r` is rolling on a smooth horizontal surface with velocity `v` and angular velocity `omega = (v=omega r)`. The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge `mu=1//5`. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View SolutionA particle of mass `'m'` is rigidly attached at `'A'` to a ring of mass `3m` and radius `'r'` . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after

View SolutionA solid sphere of mass `M` and radius `R` is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height `h` above the surface. The value of `h` so that the sphere performs pure rolling motion immediately after it has been stuck is

View Solution
Level-III questions and complete solutions for chapter SYSTEM OF PARTICLES of NARAYANA PHYSICS (HINGLISH) of Class 11