Complete Solutions to Level-V of chapter SYSTEM OF PARTICLES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES |
| NARAYANA | Level-V |
| Number Of Questions | 72 |
| Academic Year | 2023-24 |
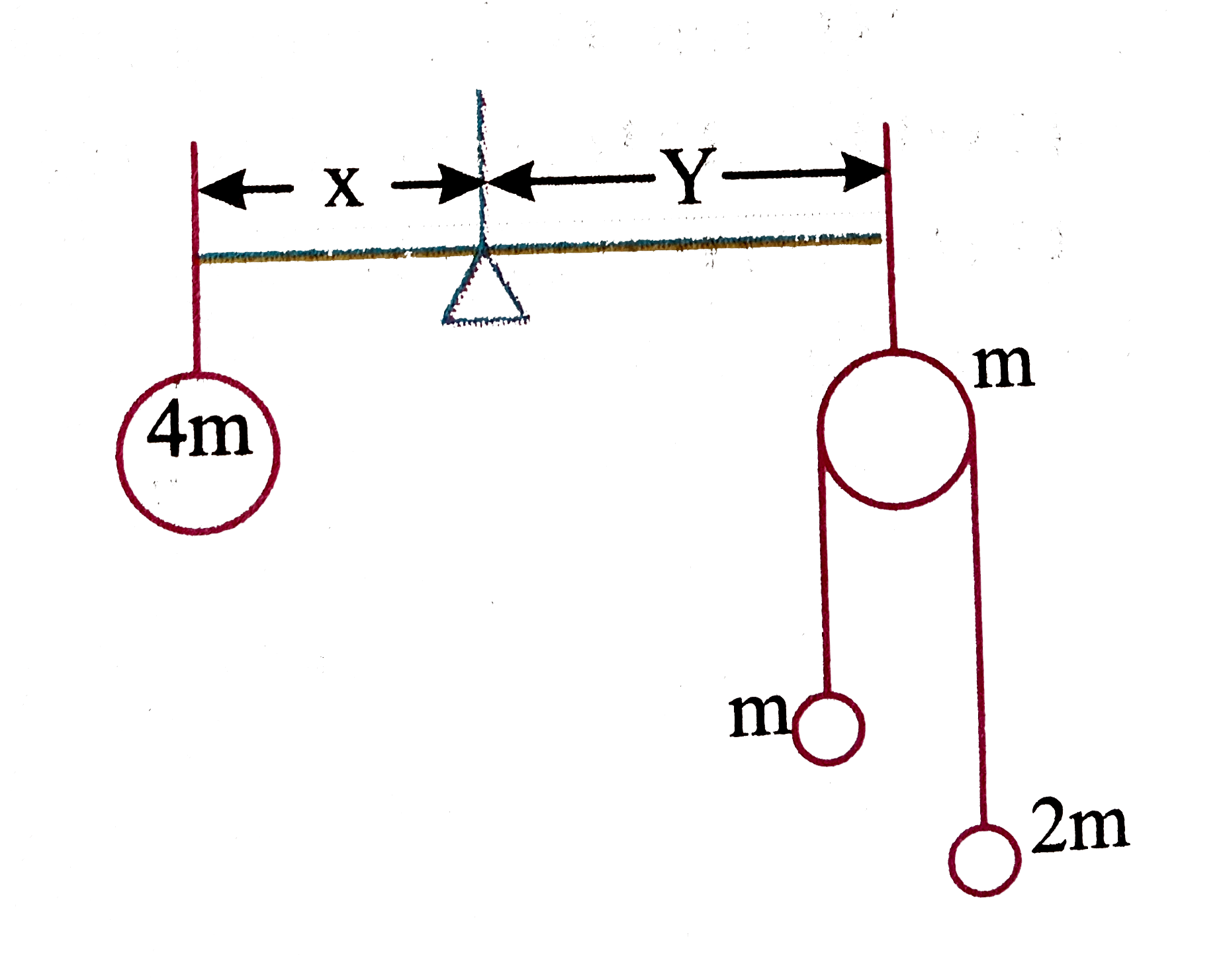
A rigid massless beam is balanced by a particle of mass `4m` in left hand side and a pulley particle system in right hand side. The value of `x/y` is
View SolutionA uniform box is kept on a rough inclined plane. It begins to topple when `theta` is equal to:

View SolutionA rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration `a`, the disc rolls on the rod without acceleration `a`, the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is

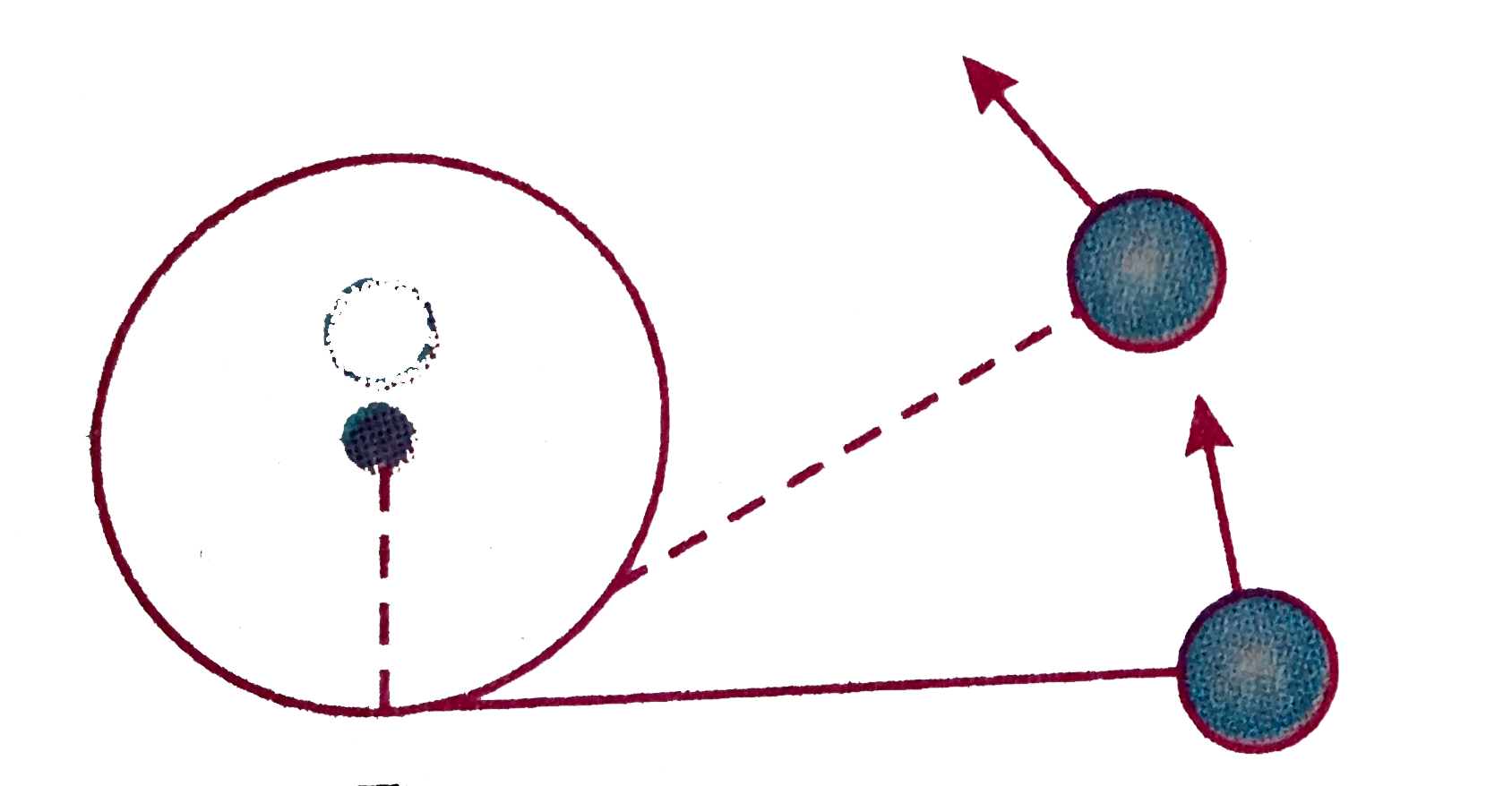
View SolutionA ball is attached to a string that is attached to a pole. When the ball is hit, the string wraps around the pole and the ball spirals inwards sliding on the frictionless surface. Neglecting air resistance, what happends as the ball swings around the pole?
View SolutionA disc of mass `m` is connected with an ideal spring of stiffness `k`. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:

View SolutionA massless thin hollow sphere is completely filled with water of mass `m`. If the hollow sphere rolls with a velocity `v`. The kinetic energy of the sphere of water is : (Assume water is non viscous)

View SolutionA particle `P` collides elastically at `M` with a speed `v`. The change in angular momentum the particle about the point `N` during collision is

View SolutionA ball is attached to a string that is attached to a pole. When the ball is hit, the string wraps around the pole and the ball spirals inwards sliding on the frictionless surface. Neglecting air resistance, what happends as the ball swings around the pole?

View SolutionThe free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity 'v' . Assuming pure rolling of bobin, find the velocity `v_(0)` of the centre of the bobbin at the instant when the thread forms an angle `alpha` with the vertical: (`R` and `r` are outer and inner radii off the babbin)

View SolutionIn the figure shown, a ring `A` is initially rolling without sliding with a velocity `1`, on the horizontal surface of the body `B` (of same mass as `A`). All surfaces arc smooth. `B` has no initial velocity. What will be the maximum height reached by `A` on `B`?

View SolutionA particle moves in a circular path with decreasing speed . Choose the correct statement.
View SolutionOn a train moving with acceleration `10 m//s^(2)`, a ball starts rolling on floor of train along the width of the train with angular acceleration `2 rad//s^(2)`, radius of ball is `1m`. Find the acceleration of the top point of ball at the time `t=3s` as seen from ground

View SolutionA hollow sphere of mass `2 kg` is kept on a rough horizontal surface. A force of `10 N` is applied at the centre of the sphere as shown in the figure. Find the minimum value of `mu` so that the sphere starts pure rolling. (take `g=10 ms^(-2)`)

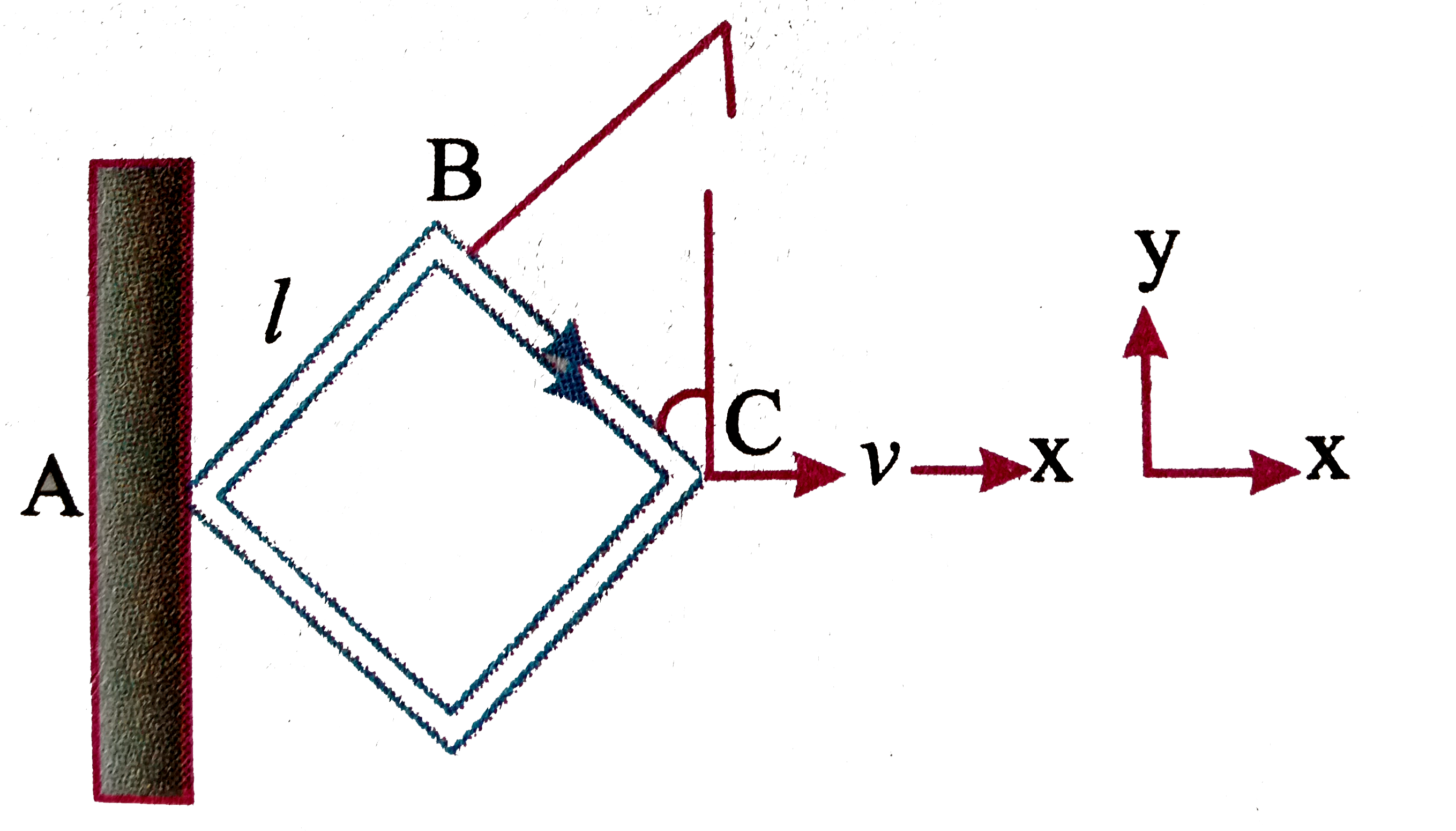
View SolutionFour rods of side length `l` have been hinged to form a rhombus. Vertex `A` is fixed to a rigid support, vertex `C` is being moved along the `x`-axis with constant velocity `V` as shown in figure. The rate at which vertex `B` is nearing the `x`-axis at the moment the rhombus is in the form of a squarem is
View SolutionA rigid body of moment of inertial `I` is projected with velocity `V` making an angle of `45^(@)` with horizontal. The magnitude of angular momentum of the projectile about the point of projection when the body is its maximum height is given by `(IV^(3))/(2sqrt(2)gR^(2))` where `R` is the radius of the rigid body. the ridid body is
View SolutionA uniform rod of length `l` is placed symmetrically on two walls as shown in Fig. The rod is in equilibrium. If `N_(1)` and `N_(2)` are the normal forces exerted by the walls on the rod, then

View SolutionOn a smooth horizontal tanle, a sphere is pressed by blocks `A` and `B` by forces `F_(1)` and `F_(2)` respectively `(F_(1)gtF_(2))` exactely normal to the tangent at the point of contact of blocks and sphere. A force `F` is applied on the sphere diameter `OP`, which is line of action of forces `F_(1)` and `F_(2)`. the sphere moves out of blocks `A` and `B`. find minimum value of `F`. the coefficient of friction is `mu` at all contancts.

View SolutionThe figure shows a uniform rod lying along the `x`-axis. The locus of all the points lying on the `xy`-plane, about which the moment of inearth, of the rod is same as that about `O`, is

View SolutionA uniform rod of length `L` (in between the supports) and mass `m` is placed on two support `A` and `B`. The rod breaks suddenly at length `L//10` from the support `B`. Find the reaction at support `A` immediately after the rod breaks

View SolutionA uniform disc of mass `m` and radius `R` is rolling up a rough inclined plane which makes an angle of `30^@` with the horizontal. If the coefficients of static and kinetic friction are each equal to `mu` and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
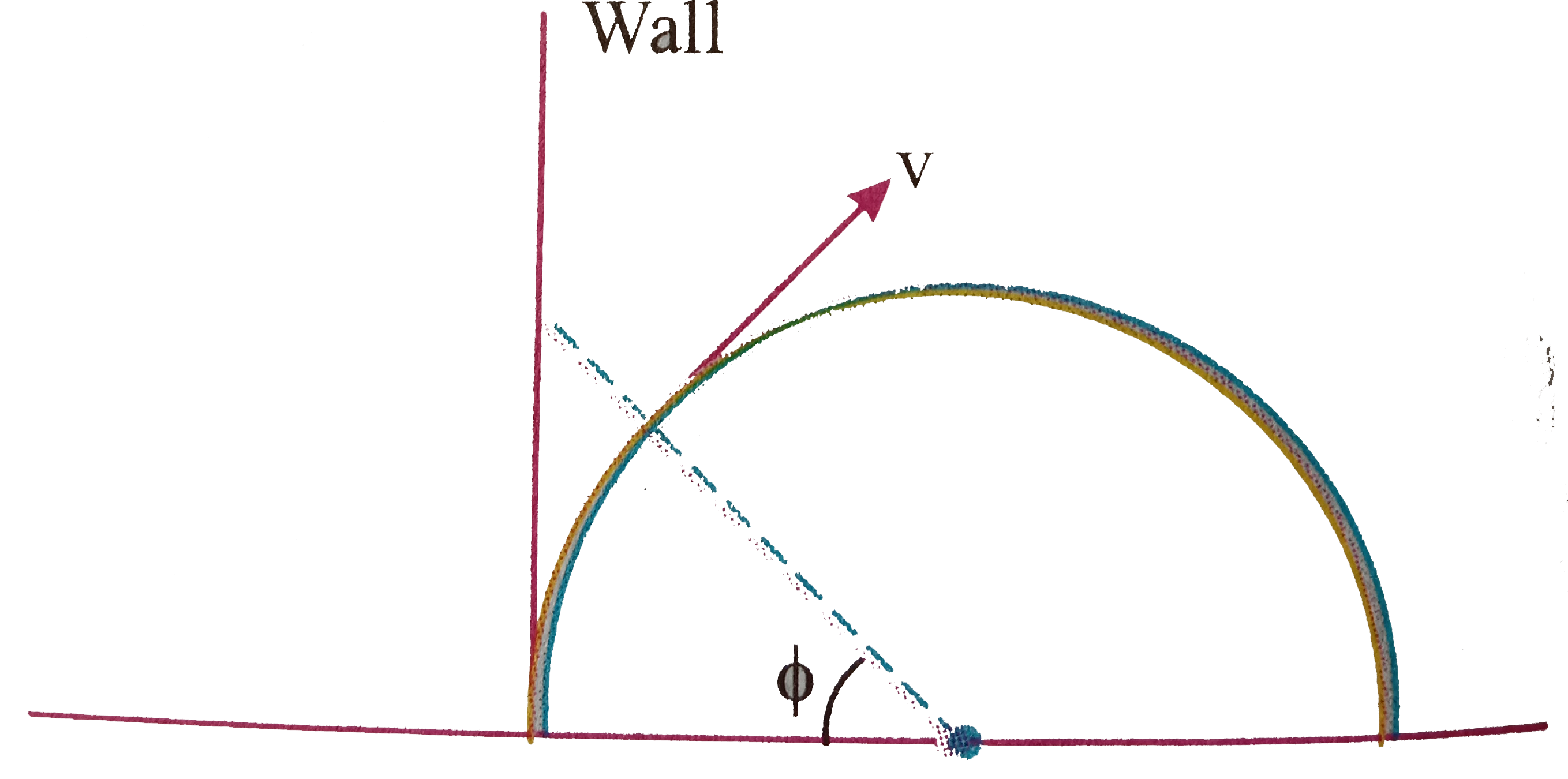
View SolutionOn a particle moving on a circular path with constant speed `v`, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
View SolutionA rod of length `l` is travelling with velocity `v` and rotating with angular velocity `omega` such that `(omegal)/2=v`. The distance travelled by end `B` of the rod when rod rotates by an angle `(pi)/2` is
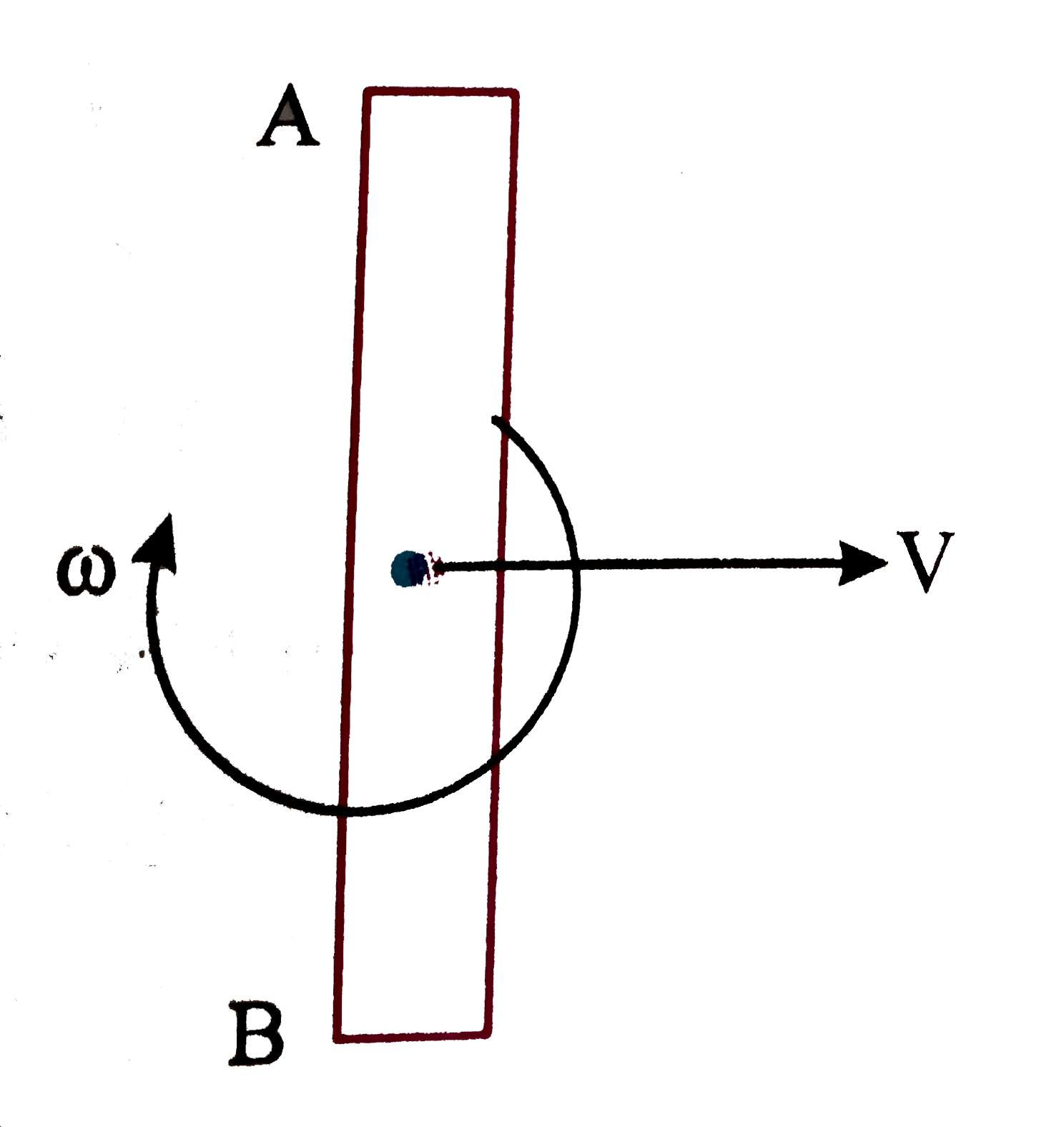
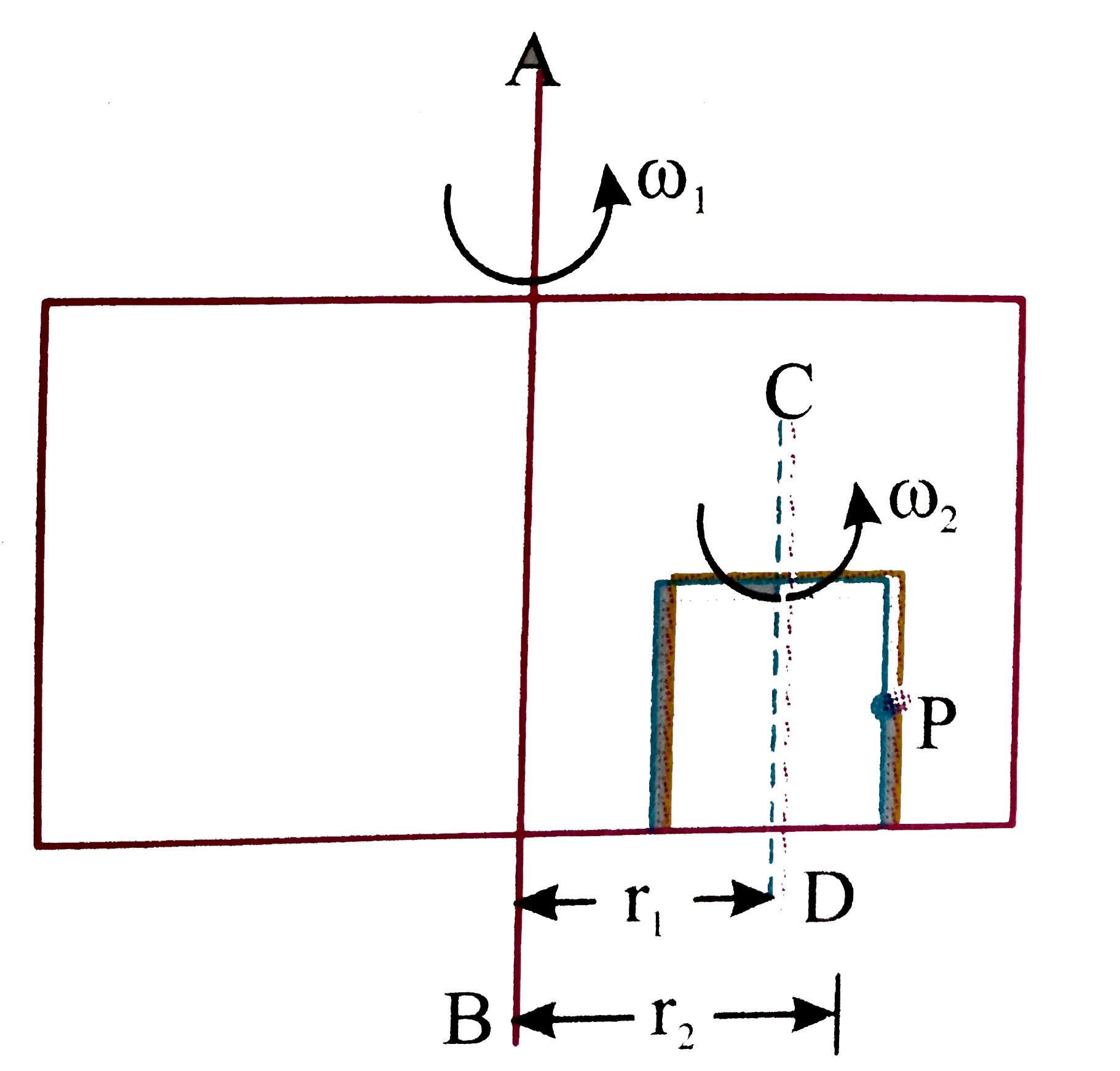
View SolutionA large rectangular box has been rotated with a constant angular velocity `omega_(1)` about its axis as shown in the figure. Another small box kept inside the bigger box is rotated in the same sense with angular velocity `omega_(2)` about its axis (which is fixed to floor of bigger box). A particle `P` has been identified, its angular velocity about `AB` would be
View SolutionTwo vertical walls are separated by a distance of `2` meters, Wall 'A' is smooth while wall `B` is rough with a coefficient of friction `mu=0.5`A uniform rod is probed between them. The length of the longest rod that can be probed between the walls is equal to
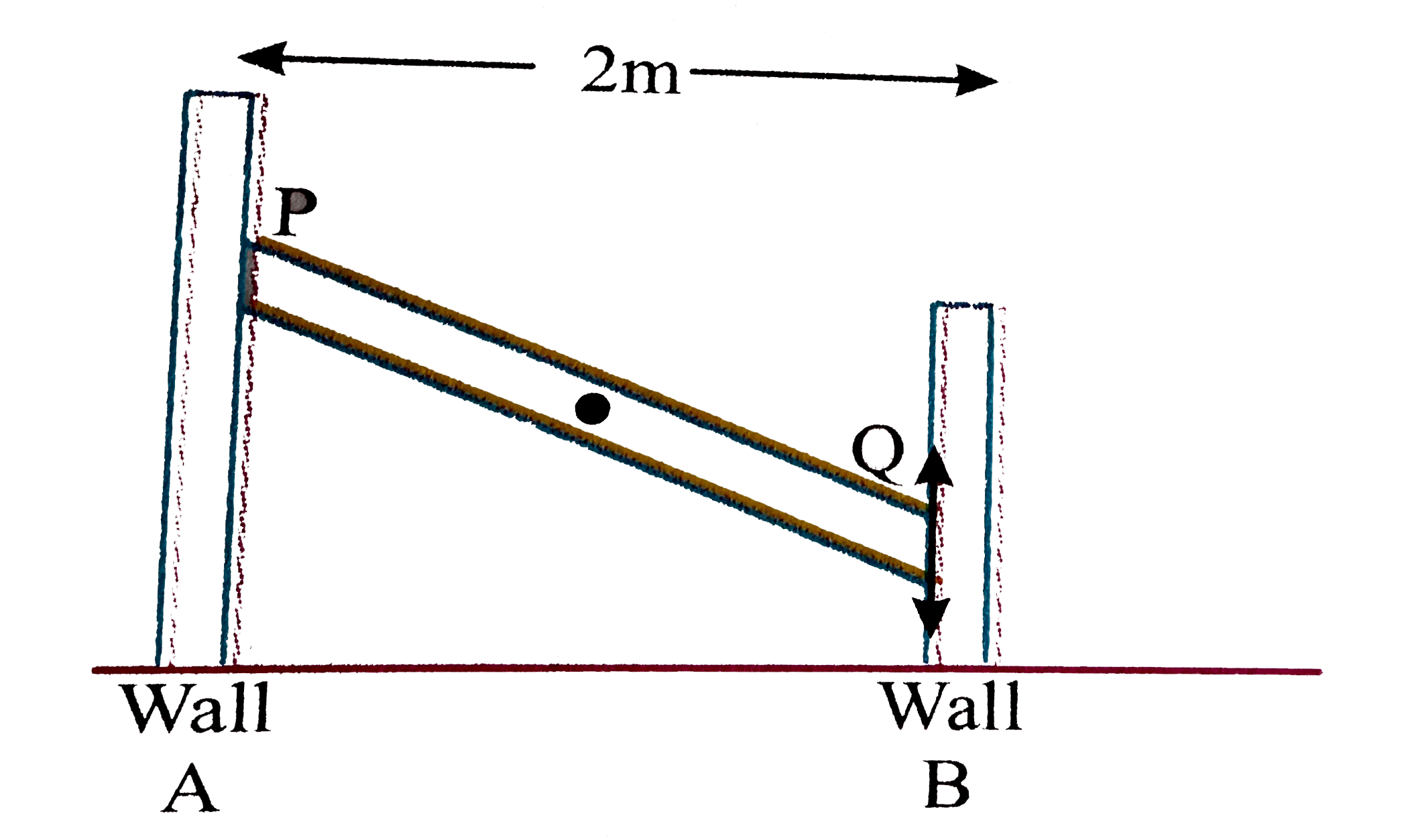
View SolutionA disc is rotating at an angular velocity `omega_(0)`. A constant retardation torque is applied on it to stop the disc. After a certain time at which some number of rotation of the disc have been performed so that total angle rotated is `theta_(1)` and that only `2/3 th` of these ratios will further stop the disc. find the retarding force.
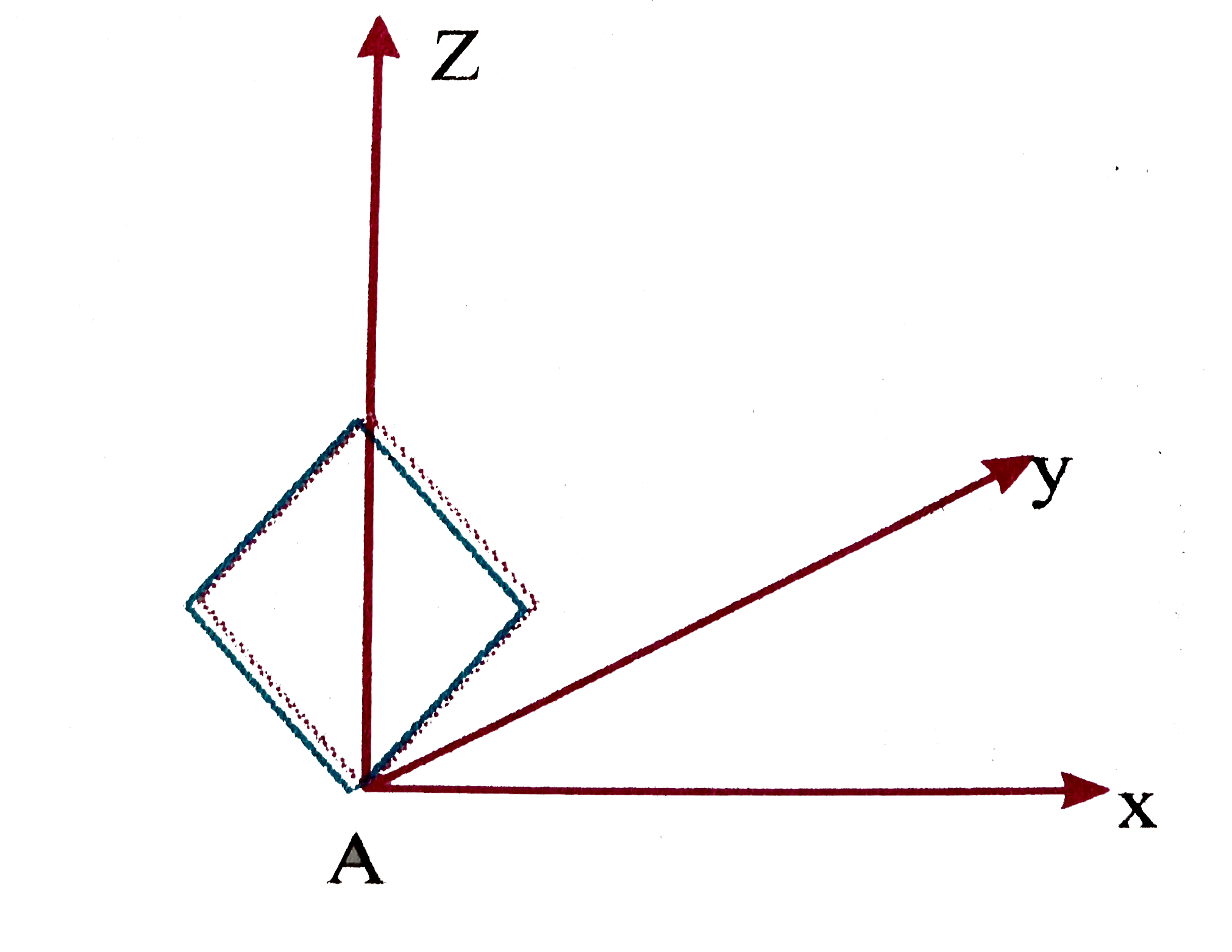
View SolutionA square plate hinged at `A`, of side a and mass `M` is placed in `(x-z)` plane. The plate is allowd to fall upto `(x-y)` plane. Find its angular velocity
View SolutionA disc of mass `m` and radius `r` placed on a routh horizontal surface. A cue of mass `m` hits the disc at a height `h` from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
View SolutionA solid cylinder is rolling down the inclined plane without slipping. Which of the following is `//` are correct
View SolutionAn impulse `I` is applied at the end of a uniform rod if mass `m`. Then:

View SolutionA thin uniform rigid rod of mass `m` and length `l` is in mechanical equilibrium under the constraints of horizontal and vertical rough surfaces. Then select correct option(s):

View SolutionA disc is given an initial angular velocity `omega_(0)` and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View SolutionA thin rod `AB` of mass `M` and length `L` is rotating with angular speed `omega_(0)` about vertically axis passing through its ends `B` on a horizontal smooth table as shown. If at some instant the hinge at end `B` of rod is opened then which of the following statemtents is `//` are correct about motion of rod?

View SolutionA cylinder rolls without slipping on a rough floor, moving with a spped `v`. It makes an elastic collision with smooth vertical wall. After impact
View SolutionA sphere of radius `0.10 m` and mass `10 kg` rests in the corner formed by a `30^(@)` inclined plane and a smooth vertical wall. Choose the correct option
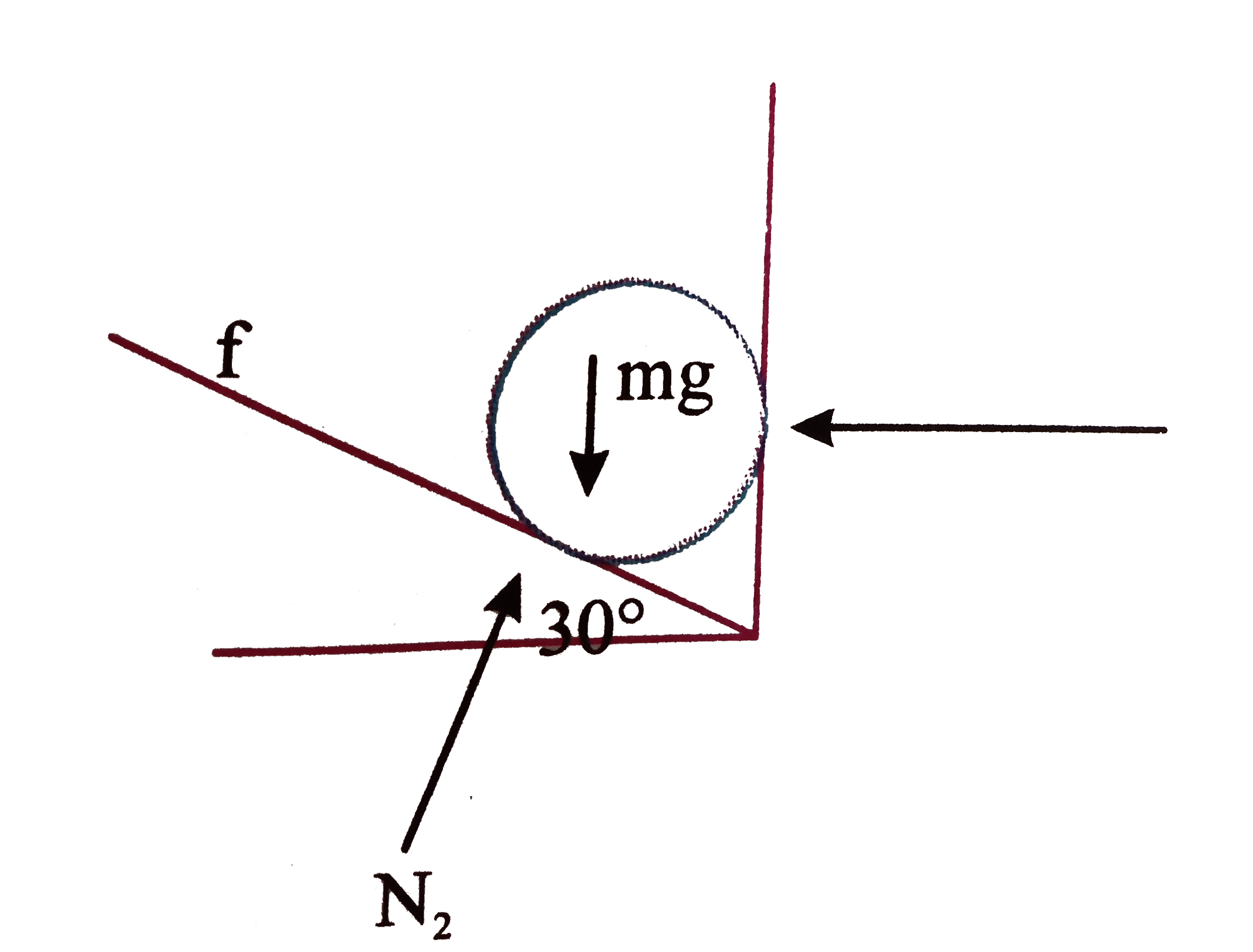
View SolutionIf the resultant of all the external forces acting on a system of particles is zero. Then from an inertial frame, one can surely say that
View SolutionA rod of length `l` is pivoted smoothly at `O` is resting on a block of height `h`. If the block moves with a constant velocity `V`, pick the current alternatives

View SolutionA solid sphere is given an angular velocity `omega` and kept on a rough fixed incline plane. The choose the correct statement.

View SolutionA string is wrapped several time on a cylinder of mass `M` and radius `R`, the cylinder is pivoted about its axis of symmetery . A block mass of `m` tied to the string rests on support so that the string is black. The block is lifted upto a height `h` and the support is removed. (shown in figure)
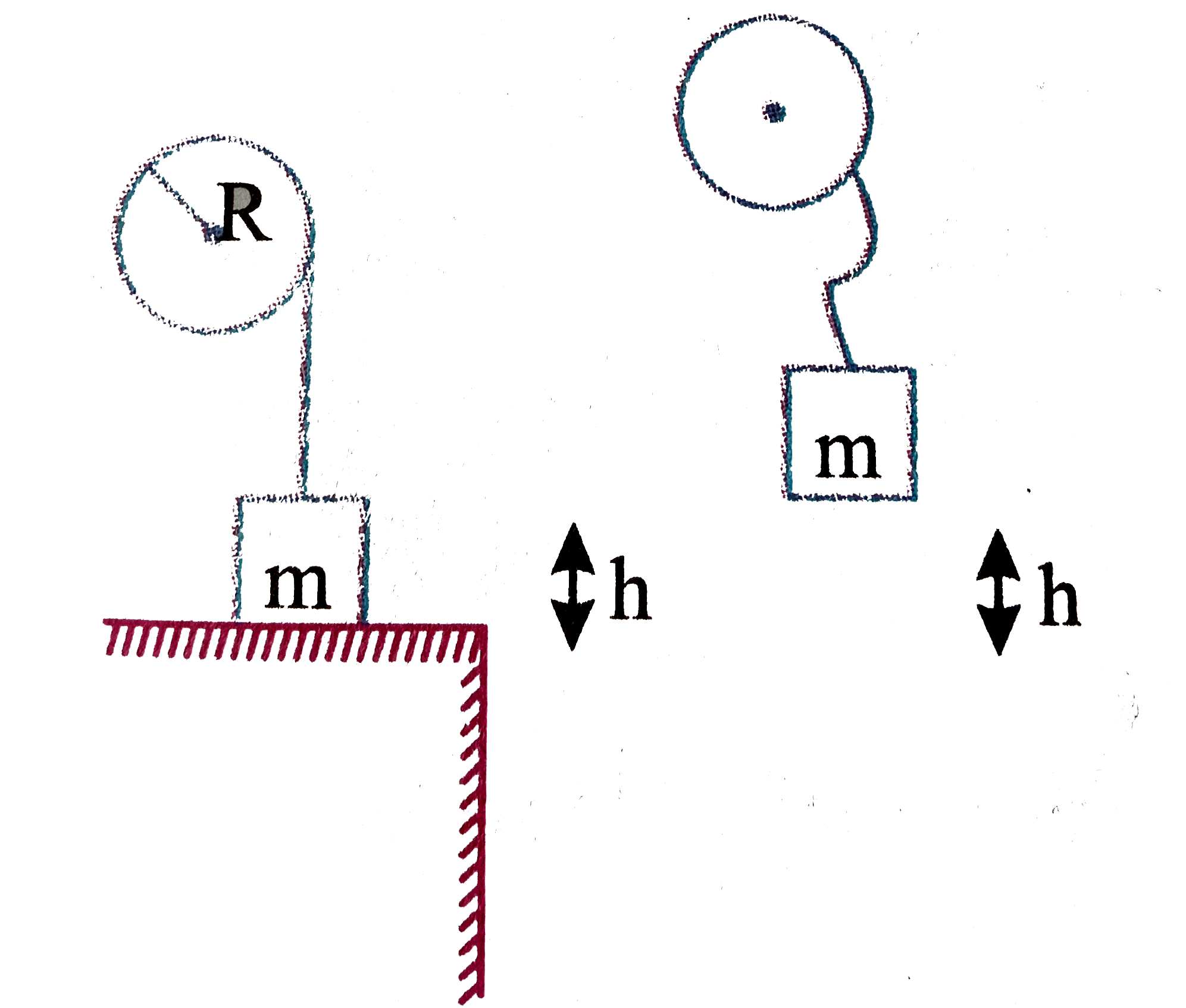
What is the angular velocity of cylinder just before the string becomes taut
View SolutionA string is wrapped several time on a cylinder of mass `M` and radius `R`, the cylinder is pivoted about its axis of symmetery . A block mass of `m` tied to the string rests on support so that the string is black. The block is lifted upto a height `h` and the support is removed. (shown in figure)
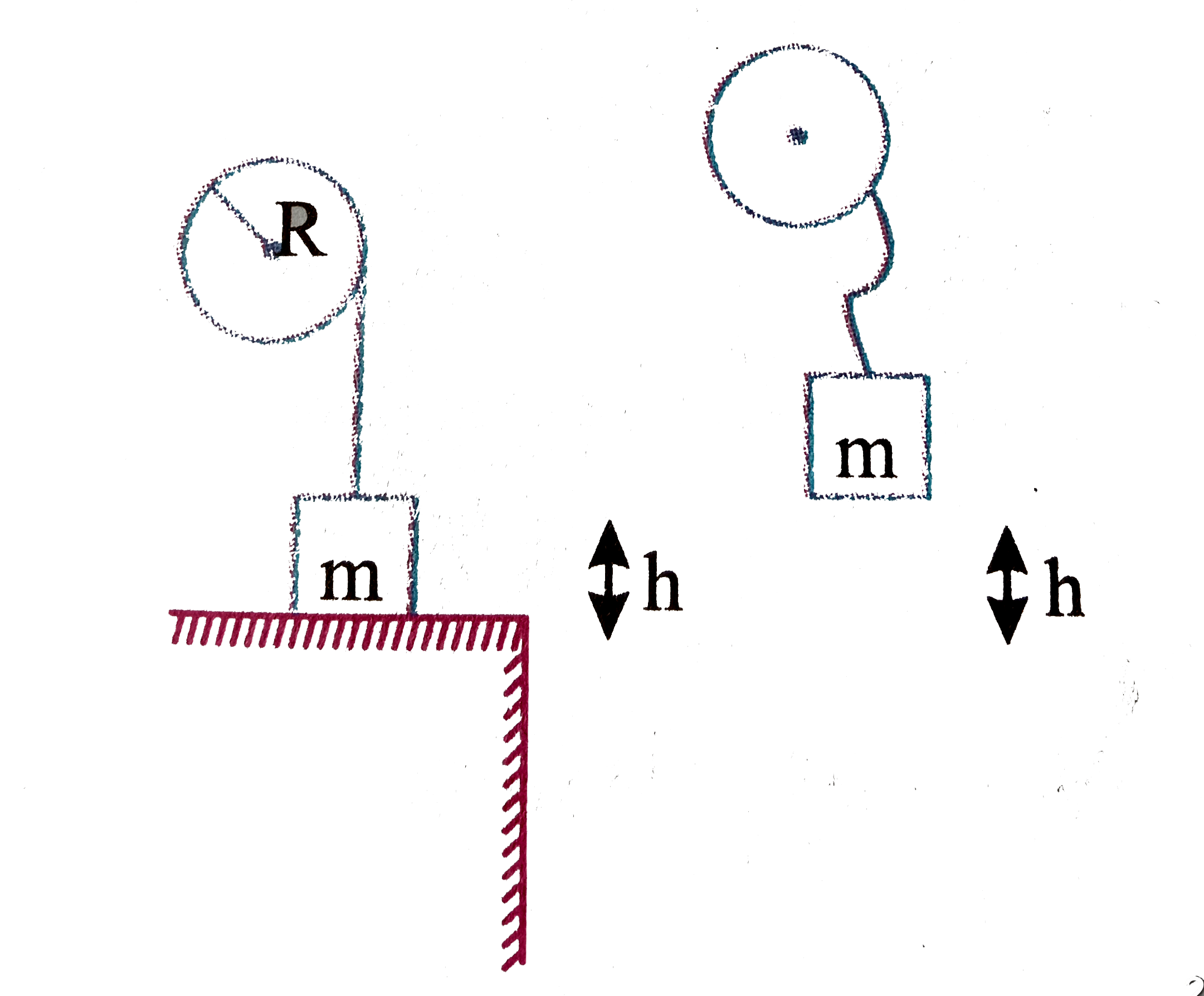
When the string experience a jerk, a large impulsive force is generated for a short duration, so that contribution of weight `mg` can be neglected suring this duration. then what will be speed of blocks `m`, just after string has becomes taut
View SolutionA string is wrapped several time on a cylinder of mass `M` and radius `R`, the cylinder is pivoted about its axis of symmetery . A block mass of `m` tied to the string rests on support so that the string is black. The block is lifted upto a height `h` and the support is removed. (shown in figure)
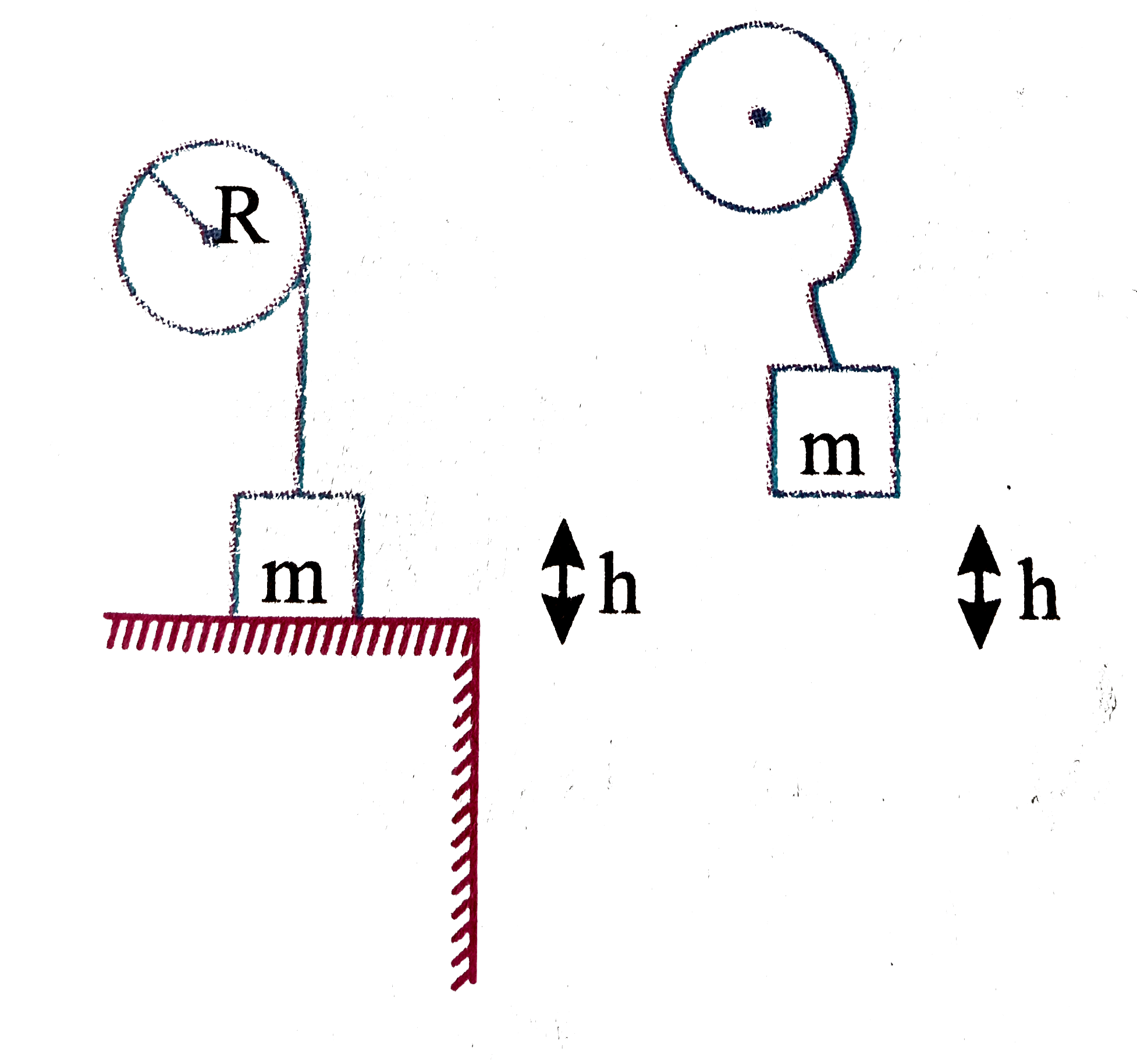
If `M=m`, what friction of `KE` is lost due to the jerk developed in the string
View SolutionA man of mass `100 kg` stands at the rim of a turtable of radius `2 m` and moment of inertia `4000 kgm^(2)` mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of `1m//s` relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
View SolutionA man of mass `100 kg` stands at the rim of a turtable of radius `2 m` and moment of inertia `4000 kgm^(2)` mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of `1m//s` relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
View SolutionA man of mass `100 kg` stands at the rim of a turtable of radius `2 m` and moment of inertia `4000 kgm^(2)` mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of `1m//s` relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity `omega` in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of `90^@`, determine V.
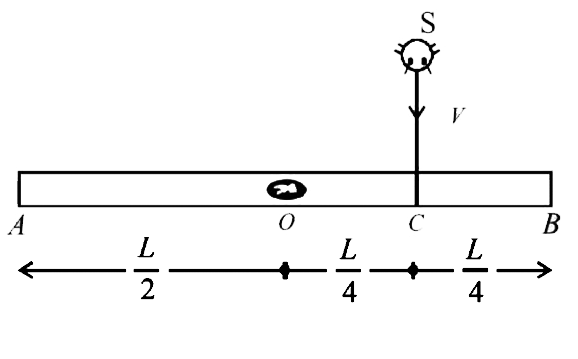
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity `omega` in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of `90^@`, determine V.

View SolutionThere particles each of mass `m` can slide on fixed frictioless circular tracks in the same horizontal plane as shown. Particle `m_(1)(=m)` moves with velocity `v_(0)` and hits particle `m_(2)(=m)`, the cofficient of restitution being `e=0.5` . Assume that `m_(2)` and `m_(3)(=m)` are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of `m_(2)` immediately after impact is
View SolutionThree particles each of mass `m` can slide on fixed friction less circular tracks in the same horizontal plane as shown. Particle `m_(1)(=m)` moves with velocity `v_(0)` and hits particle `m_(2)(=m)`, the coefficient of restitution being `e=0.5` . Assume that `m_(2)` and `m_(3)(=m)` are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of `m_(2)` immediately after impact is
View SolutionThree particles each of mass `m` can slide on fixed friction less circular tracks in the same horizontal plane as shown. Particle `m_(1)(=m)` moves with velocity `v_(0)` and hits particle `m_(2)(=m)`, the coefficient of restitution being `e=0.5` . Assume that `m_(2)` and `m_(3)(=m)` are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of `m_(2)` immediately after impact is
View SolutionIn the given figure `F=10N, R=1m`, mass of the body is `2kg` and moment of inertia of the body about an axis passing through `O` and perpendicular to the plane of the body is `4kgm^(2)`. `O` is the centre of mass of the body.

If the ground is smooth, what is the total kinetic energy of the body after `2s`?
View SolutionIn the given figure `F=10N, R=1m`, mass of the body is `2kg` and moment of inertia of the body about an axis passing through `O` and perpendicular to the plane of the body is `4kgm^(2)`. `O` is the centre of mass of the body.

If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in the given time interval of `2s`?
View SolutionA plank of length `20 m` and mass `1kg` is kept on a horizontal smooth surface. A cylinder of mass `1lg` is kept near one end of the plank. The coefficient of friction between the two surface is `0.5`. The plank is suddenly given a velocity `20 m//s` towards left

Which of the following statements is correct ?
View SolutionA plank of length `20 m` and mass `1kg` is kept on a horizontal smooth surface. A cylinder of mass `1lg` is kept near one end of the plank. The coefficient of friction between the two surface is `0.5`. The plank is suddenly given a velocity `20 m//s` towards left

Which of the following statements is correct?
View SolutionA plank of length `20 m` and mass `1kg` is kept on a horizontal smooth surface. A cylinder of mass `1lg` is kept near one end of the plank. The coefficient of friction between the two surface is `0.5`. The plank is suddenly given a velocity `20 m//s` towards left

Which of the following statements is correct?
View SolutionA plank of length `20 m` and mass `1kg` is kept on a horizontal smooth surface. A cylinder of mass `1lg` is kept near one end of the plank. The coefficient of friction between the two surface is `0.5`. The plank is suddenly given a velocity `20 m//s` towards left

Time in which plank and cylinder separate
View SolutionA circular hoop of mass `m` and radius `R` rests flat on a horizontal smooth surface. A bullet of same mass `m` and moving with velocity `upsilon` strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Mark the correct option
View SolutionA circular hoop of mass `m` and radius `R` rests flat on a horizontal smooth surface. A bullet of same mass `m` and moving with velocity `upsilon` strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of bullet in ground frame, after collision is
View SolutionA circular hoop of mass `m` and radius `R` rests flat on a horizontal smooth surface. A bullet of same mass `m` and moving with velocity `upsilon` strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of `CM` of hoop (ground frame)is
View SolutionA circular wooden hoop of mass `m` and radius `R` rests fiat on a frictionless surface. A bullet, also of mass `m` and moving with a velocity `v`, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than `R`. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
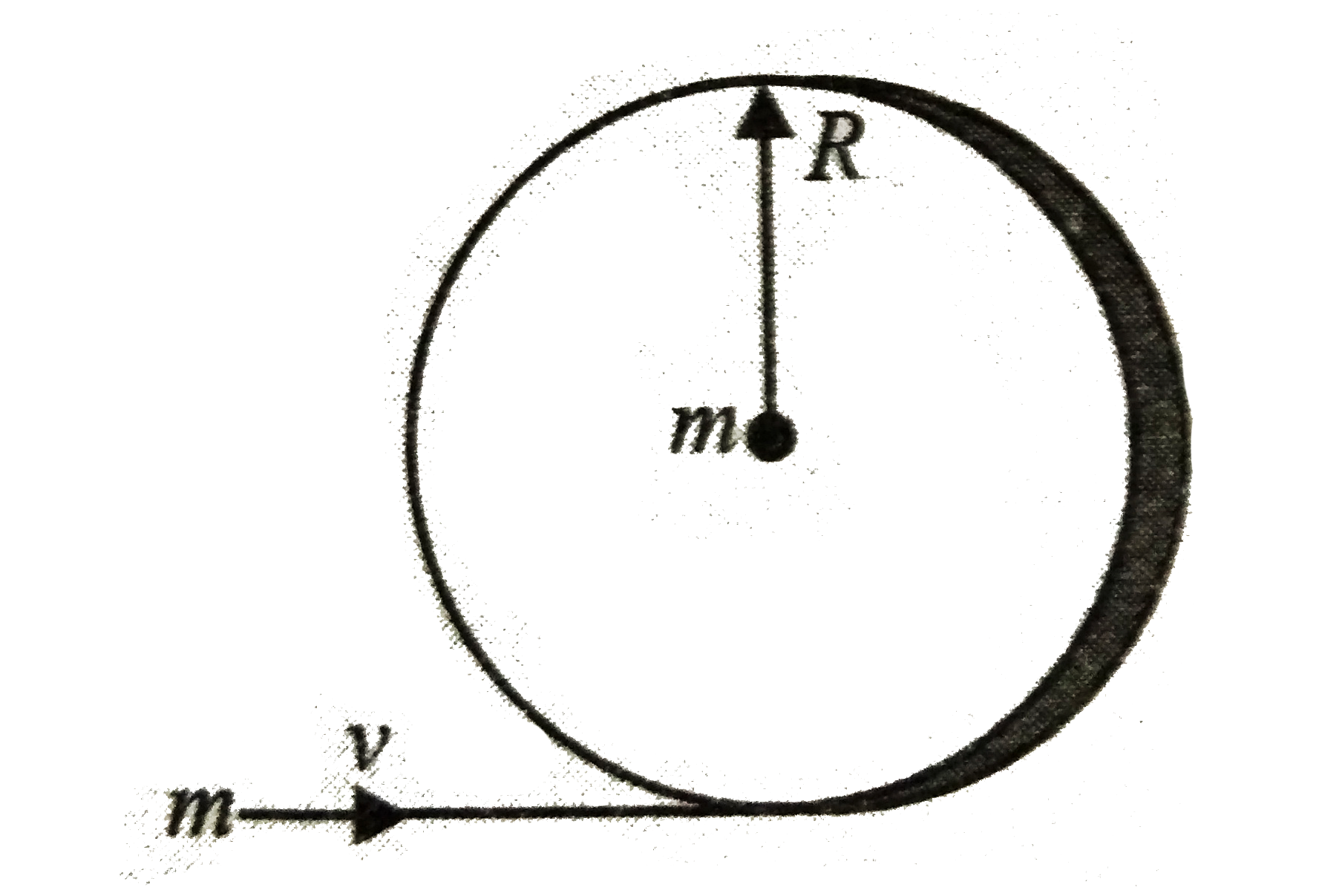
View SolutionA circular hoop of mass `m` and radius `R` rests flat on a horizontal smooth surface. A bullet of same mass `m` and moving with velocity `upsilon` strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

What is the impulse on bullet?
View SolutionA uniform rod of mass `m` is supported on two rollers each of mass `m//2` and radius `r` and rolls down the inclined rough plane as shown in the figure. Assuming no slipping at any contanct and treating the rollers as uniform solid cylinders:

If acceleration of rod down in the plane is `a_(R)` and acceleration of centre of mass of roller is `a_(o)` then:
View SolutionA uniform rod of mass `m` is supported on two rollers each of mass `m//2` and radius `r` and rolls down the inclined rough plane as shown in the figure. Assuming no slipping at any contanct and treating the rollers as uniform solid cylinders:
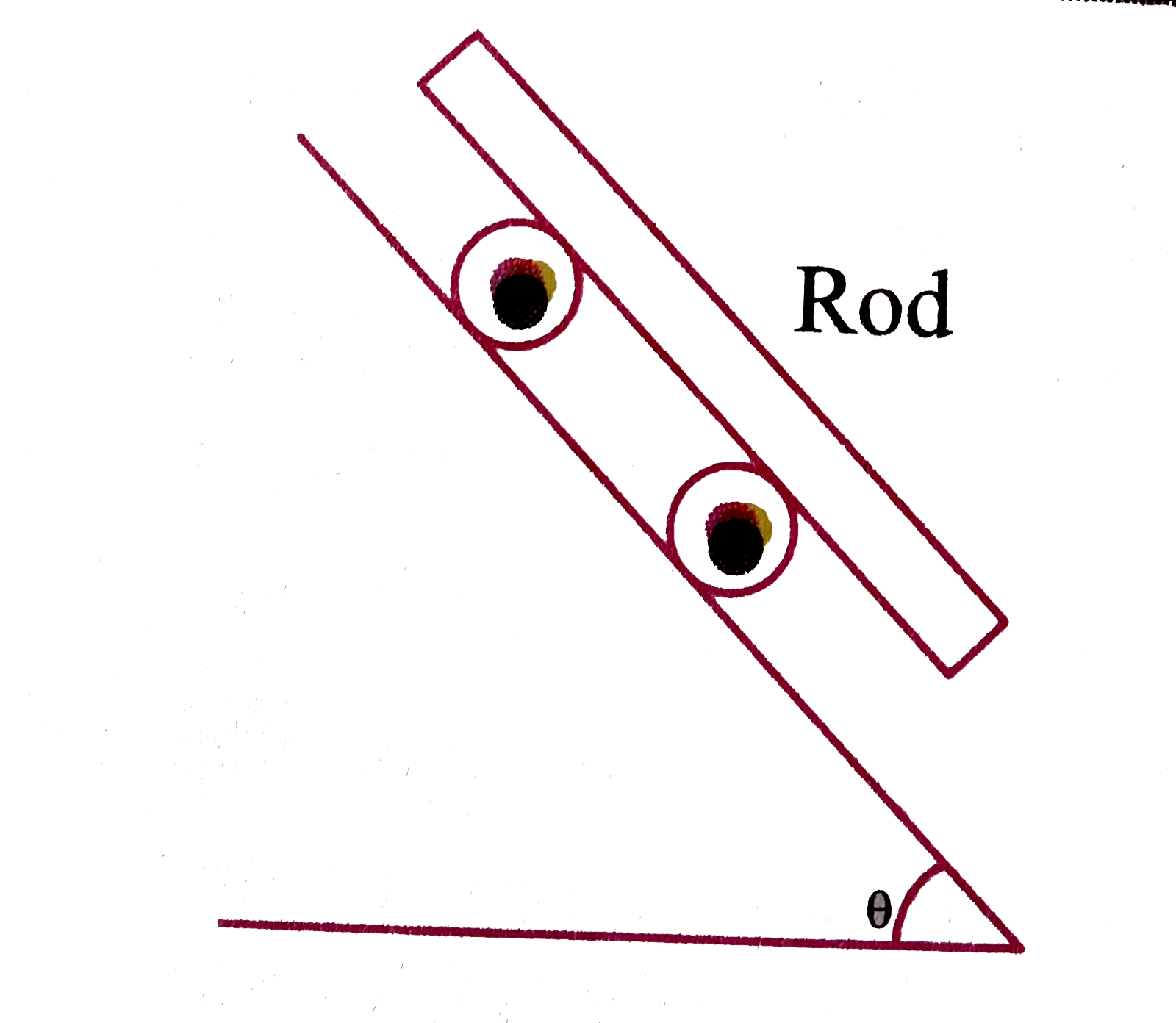
If the friction force on roller at the contanct point with incline is `f_(1)` and at the contact point with rod is `f_(2)` then:
View SolutionA uniform rod of mass `m` is supported on two rollers each of mass `m//2` and radius `r` and rolls down the inclined rough plane as shown in the figure. Assuming no slipping at any contanct and treating the rollers as uniform solid cylinders:
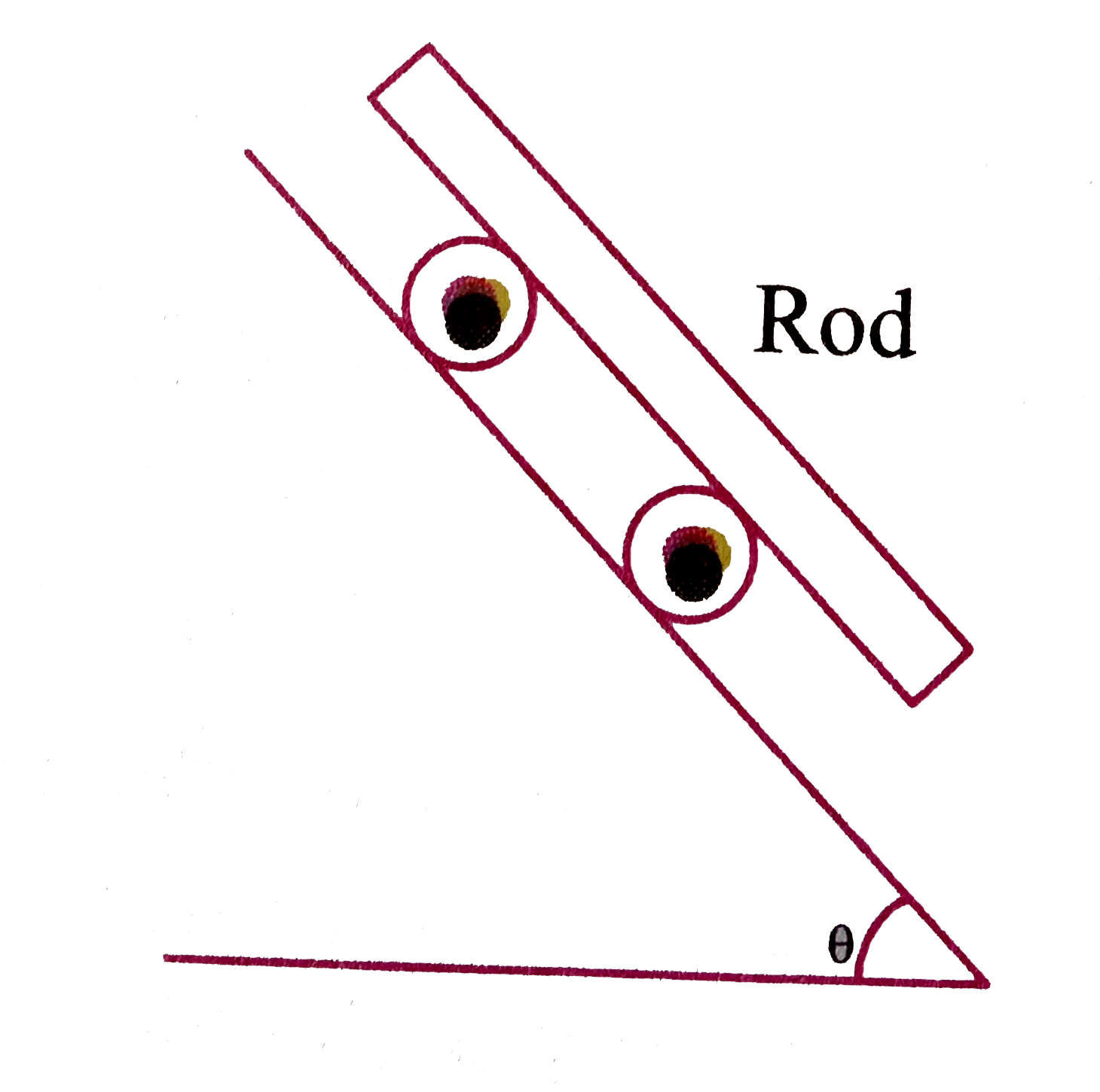
If the incline is smooth and rod still does not slip on roller, then acceleration of rollers is:
View SolutionOne end of an ideal spring of unstreched length `l_(O)=1m`, is fixed on a frictionless horizontal table. The other end has a small disc of mass `0.1 kg` attached to it. The disc is projected with a velocity `upsilon_(0)=11 m//s` perpendicular to the spring.
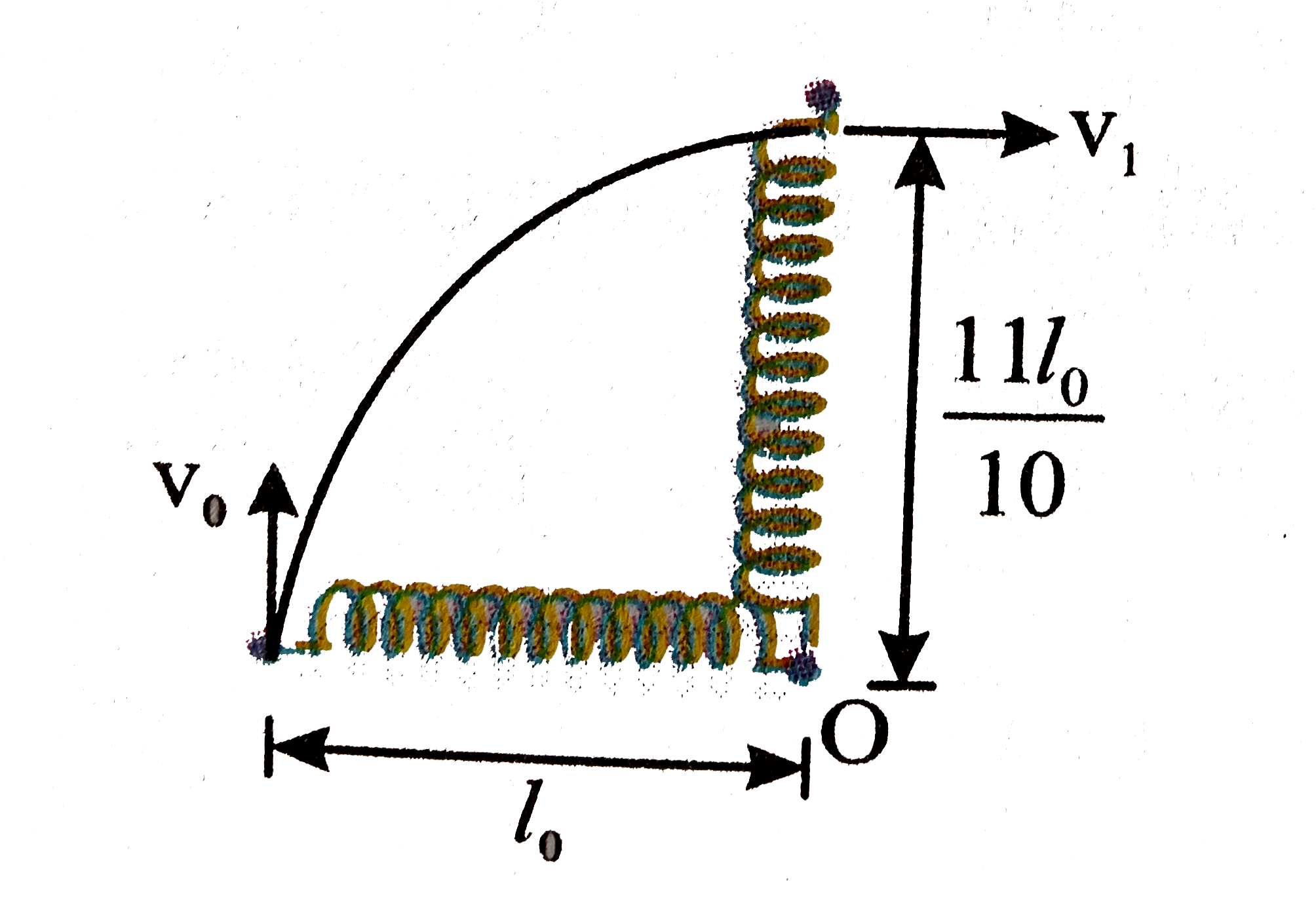
Choose the correct statements
View SolutionOne end of an ideal spring of unstreched length `l_(O)=1m`, is fixed on a frictionless horizontal table. The other end has a small disc of mass `0.1 kg` attached to it. The disc is projected with a velocity `upsilon_(0)=11 m//s` perpendicular to the spring.
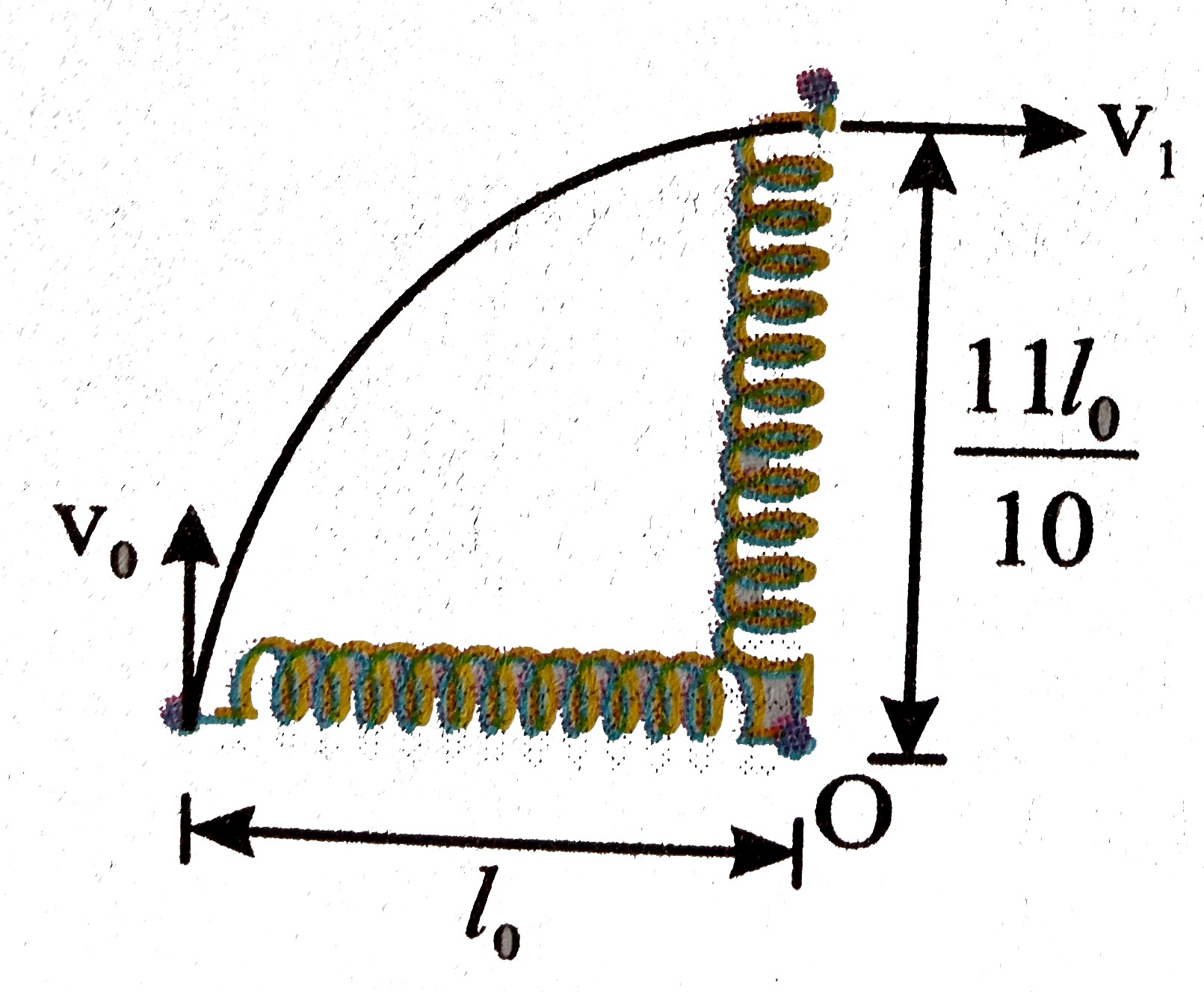
In the subsequent motion of disc, maximum elongation of spring is `11l_0//10`. the velocity of disc of this instant is:
View SolutionOne end of an ideal spring of unstreched length `l_(O)=1m`, is fixed on a frictionless horizontal table. The other end has a small disc of mass `0.1 kg` attached to it. The disc is projected with a velocity `upsilon_(0)=11 m//s` perpendicular to the spring.

What is the force constant of spring?
View SolutionA thin uniformed rod of mass `m` and length `L` is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass `2m`) and a block of mass `2m` is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of `37^(@)` with horizontal. Based on above information answer the following question :
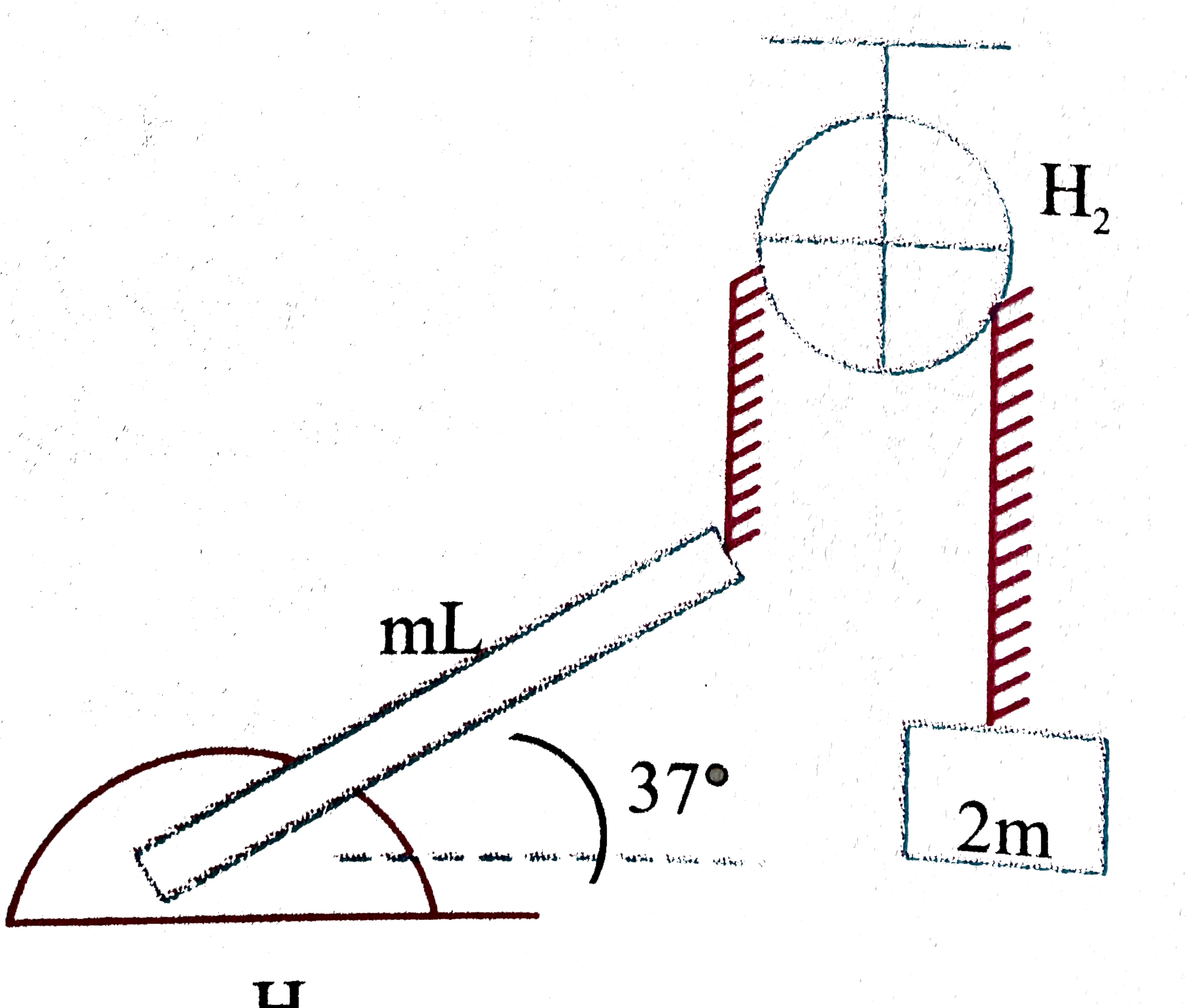
Just after releases of the system from rest acceleration of block is
View SolutionA thin uniform rod of mass `m` and length `L` is hinged at one end and from other end a light string is attached. The string is wound over a friction less pulley (having mass `2m`) and a block of mass `2m` is connected to string on other side of pulley as shown. the system is released from rest when the rod is making an angle of `37^(@)` with horizontal. Based on above information answer the following question :
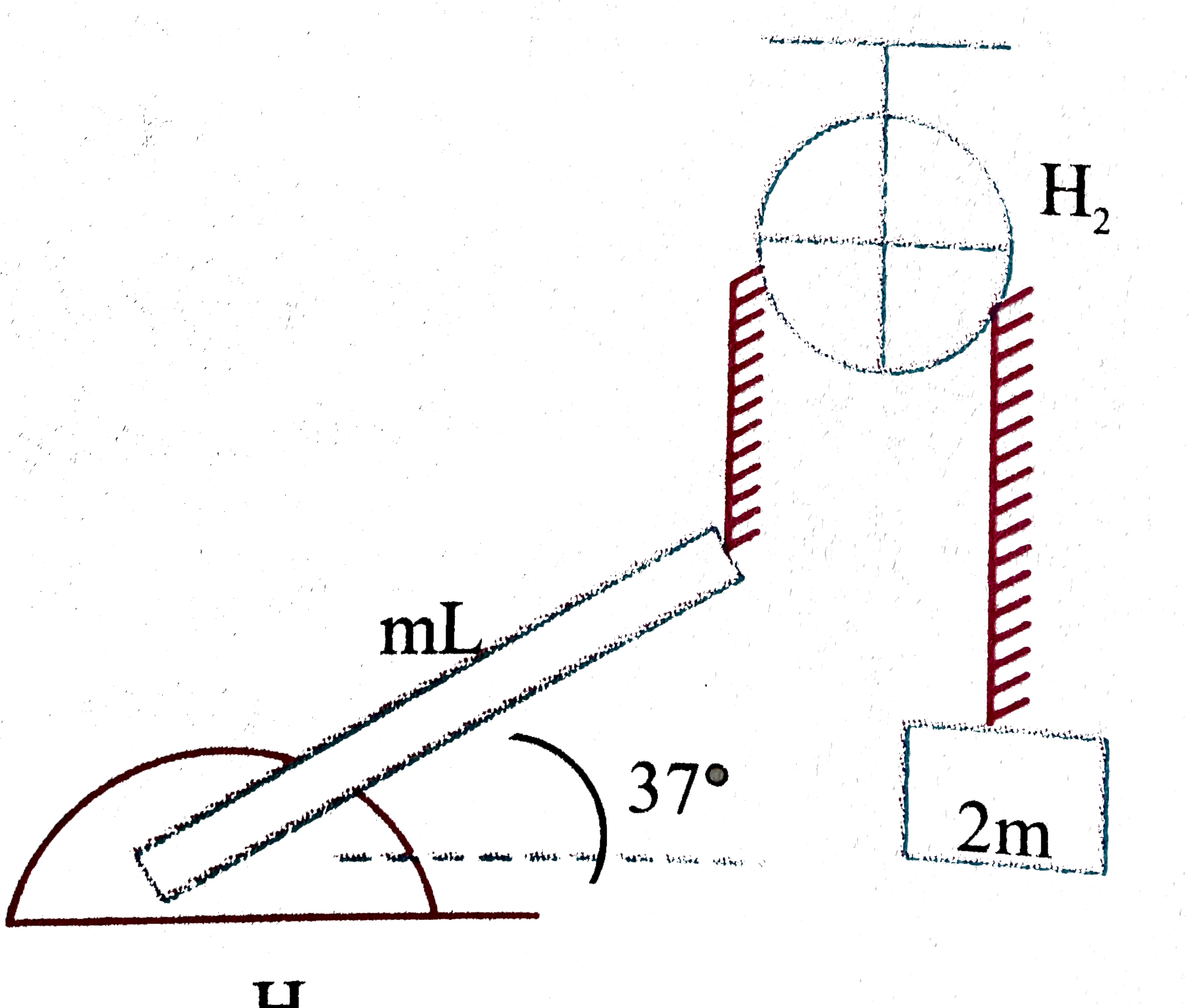
Just after release of the system from rest acceleration of block is
View SolutionA thin uniform rod of mass `m` and length `L` is hinged at one end and from other end a light string is attached. The string is wound over a friction less pulley (having mass `2m`) and a block of mass `2m` is connected to string on other side of pulley as shown. the system is released from rest when the rod is making an angle of `37^(@)` with horizontal. Based on above information answer the following question :
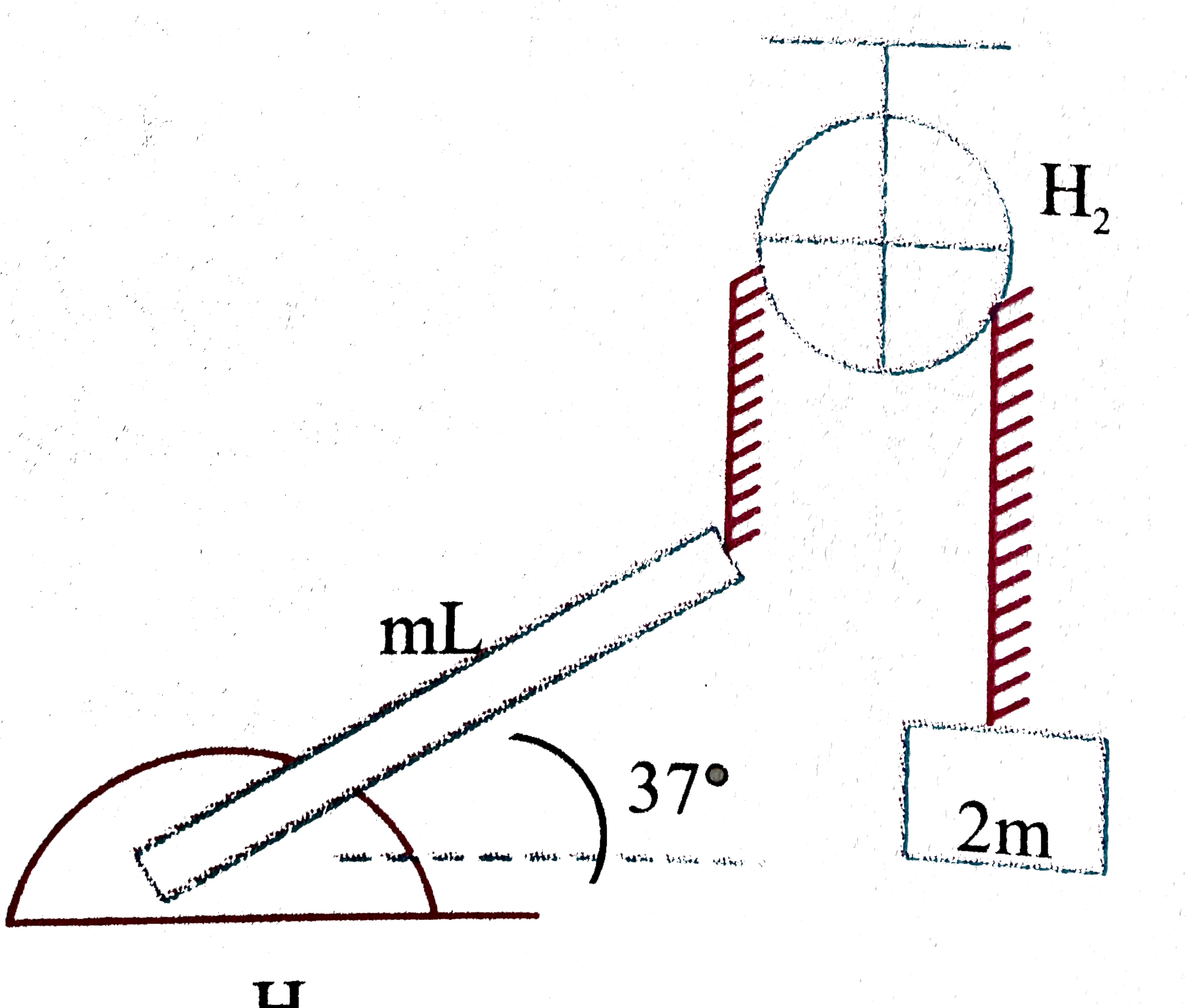
Just after release of the system from rest acceleration of block is
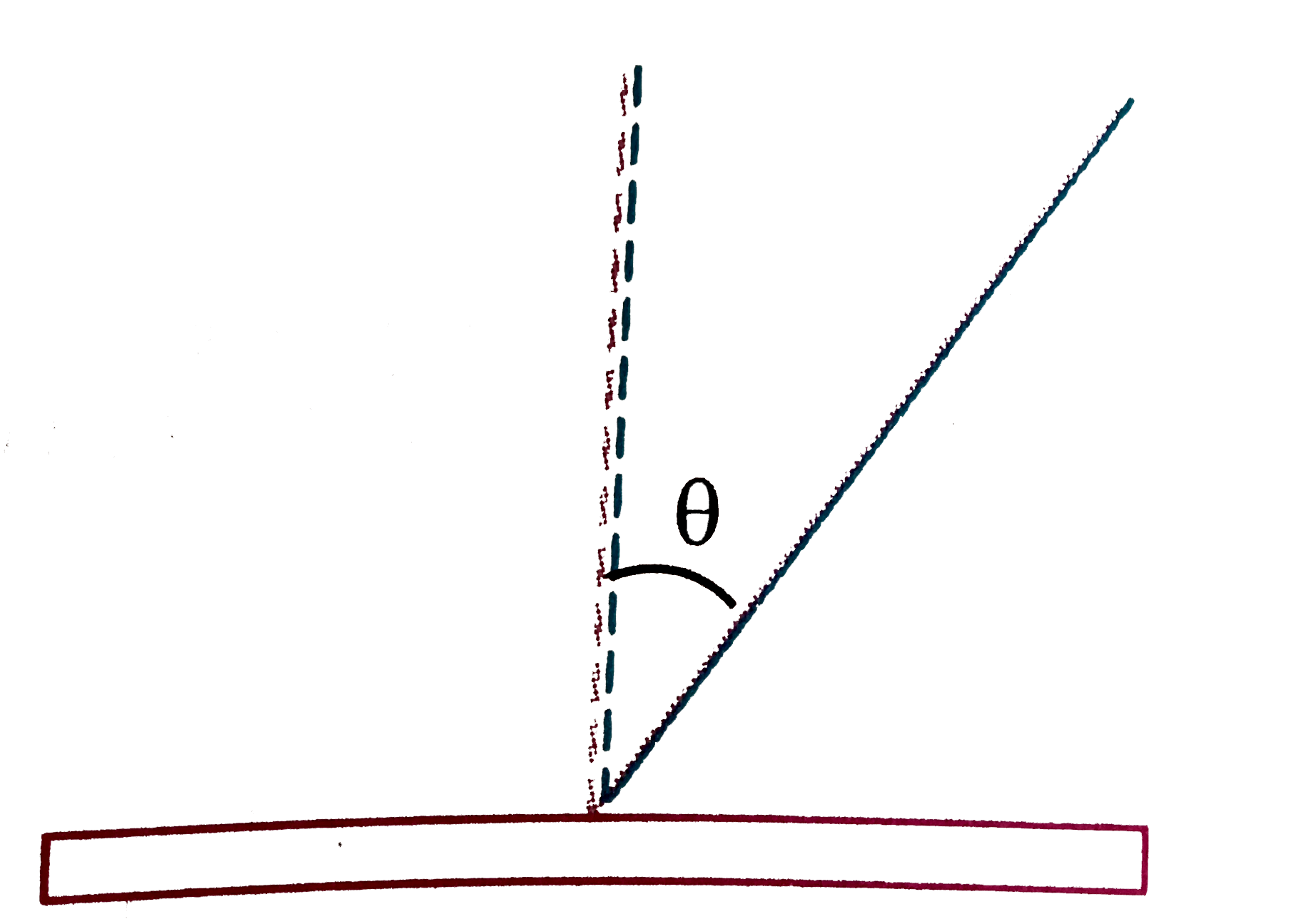
View SolutionA rod of mass `m` and length `l` is released from rest from vertical position as shown in the figure. The normal force as a function of `theta`, which is exerted on the rod by the ground as it falls downwards, assuming that it does not slip is `mg((3 cos theta-1)/n)^(2)` then `n=`
View SolutionOne end of a uniform rod of mass `M` and length `L` is supproted by a frictionless hinge which can with stand a tension of `1.75 Mg`. The rod is free to rotate in a vertical plane. The maximum angle should the rod be rotated from the vertical position so that when left, the hinge does not brek is `(pi)/n`
View SolutionA thin uniform bar of mass `m` and length `2L` is held at angle `30^(@)` with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing immediately after string breaks is

View SolutionA uniform sphere of radius `R/16` starts rolling down without slipping from the top of another sphere of radius `R=1m`. The angular velocity of the sphere of in rad`s^(-1)`, after it leaves the surface of the larger sphere is `8 xn`. Where `n`=--`
View Solution
Level-V questions and complete solutions for chapter SYSTEM OF PARTICLES of NARAYANA PHYSICS (HINGLISH) of Class 11